Θεωρία Galois
Ενότητες
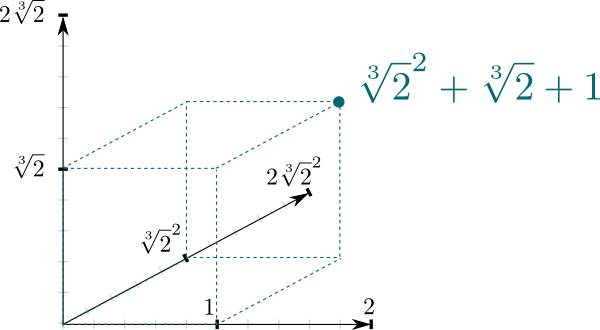
Αναπτύσσεται η βασική θεωρία των επεκτάσεων σωμάτων. Ως εφαρμογή, αποδεικνύεται το αδύνατο ορισμένων γεωμετρικών κατασκευών με κανόνα και διαβήτη. Ορίζονται τα σώματα ριζών πολυωνύμων.
Λέξεις κλειδιά: επεκτάσεις, γεωμετρικές κατασκευές, σώμα ριζών
Βιντεοσκοπημένες Διαλέξεις | ||
| Επέκταση σύνολου σημείων του επιπέδου Εφαρμογές, τριχοτόμηση γωνίας. |
||
| Επεκτάσεις σωμάτων και γεωμετρικές κατασκευές Εισαγωγή συντεταγμένων, Λήμμα. Περιπτώσεις. |
||
| Παραδείγματα υπολογισμού βαθμού επεκτάσεων Πως σχετίζονται με τις γεωμετρικές κατασκευές με κανόνα και διαβήτη: εισαγωγή. |
||
| Αλγεβρικό στοιχείο και ελάχιστο πολυώνυμο: συνέχεια Παραδείγματα, ανάγωγο πολυώνυμο και βαθμός επέκτασης. |
||
| Αλγεβρικό στοιχείο και ελάχιστο πολυώνυμο Λήμμα, βαθμός επέκτασης και βαθμός πολυωνύμου. Απόδειξη, παραδείγματα. |
||
| Αλγεβρικά και Υπερβατικά στοιχεία Ορισμοί. Ελάχιστο πολυώνυμο. |
||
| Επεκτάσεις σωμάτων: βαθμός επέκτασης Παραδείγματα, προτάσεις και πορίσματα. |
||
| Σώματα ριζών Συνέχεια στην επέκταση σύνολου σημείων του επιπέδου: κατασκευή κανονικού n-γώνου. Σώματα ριζών: προτάσεις. |
||
| Σώματα ριζών: συνέχεια Κατασκευή επέκτασης σωμάτων αναζητώντας ρίζες. Σώμα ριζών πολυωνύμων: ύπαρξη, μοναδικότητα, ιδιότητες. |
||
| Σώμα ριζών πολυωνύμου Ισομορφισμός σωμάτων. |
||
| Ισομορφισμός σωμάτων Παρατηρήσεις, προτάσεις. Ισομορφισμός σωμάτων και μεταθετικό διάγραμμα. |
||
| Ισομορφισμός σωμάτων: συνέχεια Πως επεκτείνονται οι ισομορφισμοί. Πως επεκτείνεται η ταυτοτική απεικόνιση. Εισαγωγή στον Αυτομορφισμό σωμάτων. |
||
