Θεωρία Galois
Ιωάννης Εμμανουήλ
Ο στόχος του μαθήματος είναι να εισάγει τους φοιτητές στη θεωρία των επεκτάσεων και των αυτομορφισμών σωμάτων, καθώς επίσης και να περιγράψει ορισμένες κλασικές εφαρμογές της θεωρίας.
Λιγότερα
Ο στόχος του μαθήματος είναι να εισάγει τους φοιτητές στη θεωρία των επεκτάσεων και των αυτομορφισμών σωμάτων, καθώς επίσης και να περιγράψει ορισμένες κλασικές εφαρμογές της θεωρίας.
Ο στόχος του μαθήματος είναι να εισάγει τους φοιτητές στη θεωρία των επεκτάσεων και των αυτομορφισμών σωμάτων, καθώς επίσης και να περιγράψει ορισμένες κλασικές εφαρμογές της θεωρίας.
Περίγραμμα

Διδάσκοντες
Εμμανουήλ Ιωάννης
Θέση : Καθηγητής
Τομέας : Άλγεβρας-Γεωμετρίας, Τμήμα Μαθηματικών
Ερευνητικά Ενδιαφέροντα : Άλγεβρα
Σύντομο Βιογραφικό σημείωμα
Σπούδασα μαθηματικά στο Πανεπιστήμιο Αθηνών και συνέχισα τις σπουδές μου στο Πανεπιστήμιο της California στο Berkeley. Δίδαξα για τρία έτη στο Πανεπιστήμιο του Michigan στο Ann Arbor και εργάστηκα για ένα έτος στο IHES στη Γαλλία. Επέστρεψα στην Ελλάδα και διορίστηκα στο Πανεπιστήμιο Αθηνών, όπου και εργάζομαι. Τα ερευνητικά μου ενδιαφέροντα επικεντρώνονται στην Άλγεβρα.
Περιεχόμενο μαθήματος
Στο μάθημα καλύπτονται τα εξής θέματα:
- Βασικά στοιχεία της θεωρίας των δακτυλίων πολυωνύμων
- Σώματα και επεκτάσεις, κατασκευές με κανόνα και διαβήτη, σώματα ριζών πολυωνύμων
- Αυτομορφισμοί σωμάτων, η αντιστοιχία Galois, επιλυσιμότητα εξισώσεων με ριζικά
Μαθησιακοί στόχοι
Οι φοιτητές μαθαίνουν πώς οι τεχνικές της αφηρημένης άλγεβρας μπορούν να χρησιμοποιηθούν για να προσεγγιστούν κλασικά προβλήματα, όπως οι κατασκευές με κανόνα και διαβήτη και η εύρεση τύπων για τις ρίζες πολυωνύμων.
Προτεινόμενα συγγράμματα
- Θεωρία Galois, Στ. Ανδρεαδάκη
Επιπλέον συνιστώμενη βιβλιογραφία και υλικό προς μελέτη
- Συγγράμματα που προσφέρονται μέσω του συστήματος ΕΥΔΟΞΟΣ
- Θεωρία Galois, Στ. Ανδρεαδάκη
- Άλλα βιβλία (Textbooks)
- Galois Theory, J. Rotman
Προαπαιτούμενα
Γενικές προαπαιτούμενες γνώσεις:
- Γραμμική Άλγεβρα, Θεωρία Δακτυλίων
- Κωδικοί προαπαιτούμενων μαθημάτων του Τμήματος: 121, 221, 421
Ομάδα στόχος
Υποψήφιοι και εν ενεργεία φοιτητές/φοιτήτριες, και απόφοιτοι Τμημάτων Μαθηματικών.
Ενδιαφερόμενοι για τη θεματική περιοχή Άλγεβρα.
Εμμανουήλ Ιωάννης
Θέση : Καθηγητής
Τομέας : Άλγεβρας-Γεωμετρίας, Τμήμα Μαθηματικών
Ερευνητικά Ενδιαφέροντα : Άλγεβρα
Σύντομο Βιογραφικό σημείωμα
Σπούδασα μαθηματικά στο Πανεπιστήμιο Αθηνών και συνέχισα τις σπουδές μου στο Πανεπιστήμιο της California στο Berkeley. Δίδαξα για τρία έτη στο Πανεπιστήμιο του Michigan στο Ann Arbor και εργάστηκα για ένα έτος στο IHES στη Γαλλία. Επέστρεψα στην Ελλάδα και διορίστηκα στο Πανεπιστήμιο Αθηνών, όπου και εργάζομαι. Τα ερευνητικά μου ενδιαφέροντα επικεντρώνονται στην Άλγεβρα.
Στο μάθημα καλύπτονται τα εξής θέματα:
- Βασικά στοιχεία της θεωρίας των δακτυλίων πολυωνύμων
- Σώματα και επεκτάσεις, κατασκευές με κανόνα και διαβήτη, σώματα ριζών πολυωνύμων
- Αυτομορφισμοί σωμάτων, η αντιστοιχία Galois, επιλυσιμότητα εξισώσεων με ριζικά
Οι φοιτητές μαθαίνουν πώς οι τεχνικές της αφηρημένης άλγεβρας μπορούν να χρησιμοποιηθούν για να προσεγγιστούν κλασικά προβλήματα, όπως οι κατασκευές με κανόνα και διαβήτη και η εύρεση τύπων για τις ρίζες πολυωνύμων.
- Θεωρία Galois, Στ. Ανδρεαδάκη
- Συγγράμματα που προσφέρονται μέσω του συστήματος ΕΥΔΟΞΟΣ
- Θεωρία Galois, Στ. Ανδρεαδάκη
- Άλλα βιβλία (Textbooks)
- Galois Theory, J. Rotman
Γενικές προαπαιτούμενες γνώσεις:
- Γραμμική Άλγεβρα, Θεωρία Δακτυλίων
- Κωδικοί προαπαιτούμενων μαθημάτων του Τμήματος: 121, 221, 421
Υποψήφιοι και εν ενεργεία φοιτητές/φοιτήτριες, και απόφοιτοι Τμημάτων Μαθηματικών.
Ενδιαφερόμενοι για τη θεματική περιοχή Άλγεβρα.

Γίνεται μια σύντομη επισκόπηση των απαραίτητων στοιχείων από τη θεωρία των δακτυλίων και ειδικότερα των δακτυλίων πολυωνύμων.
Λέξεις κλειδιά: πολυώνυμα
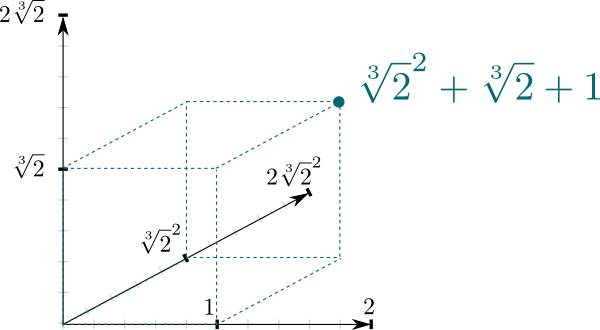
Αναπτύσσεται η βασική θεωρία των επεκτάσεων σωμάτων. Ως εφαρμογή, αποδεικνύεται το αδύνατο ορισμένων γεωμετρικών κατασκευών με κανόνα και διαβήτη. Ορίζονται τα σώματα ριζών πολυωνύμων.
Λέξεις κλειδιά: επεκτάσεις, γεωμετρικές κατασκευές, σώμα ριζών
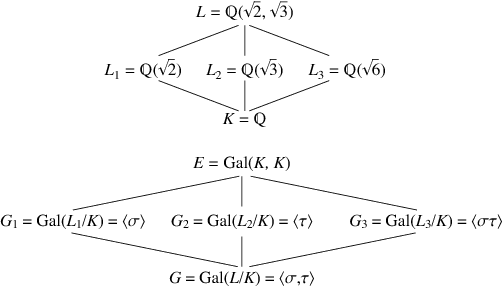
Ορίζεται η ομάδα των αυτομορφισμών ενός σώματος και οι κανονικές επεκτάσεις. Αποδεικνύεται το θεμελιώδες θεώρημα της θεωρίας και εξετάζεται η επιλυσιμότητα των πολυωνυμικών εξισώσεων με ριζικά.
Λέξεις κλειδιά: αυτομορφισμοί σώματος, αντιστοιχία Galois, επίλυση με ριζικά
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -

