Γραφικά με Ηλεκτρονικούς Υπολογιστές
Μαριλένα Μητρούλη
Τα θέματα τα οποία καλύπτονται στο μάθημα είναι:
- Αλγόριθμοι σχεδιασμού βασικών γεωμετρικών σχημάτων
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους. - Μετασχηματισμοί στο επίπεδο και στο χώρο των τριών διαστάσεων
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους. - Αλγόριθμοι αποκοπής καθώς και το πεδίο παράστασης (Viewport)
Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους. - Απεικονίσεις χώρου σε επίπεδο
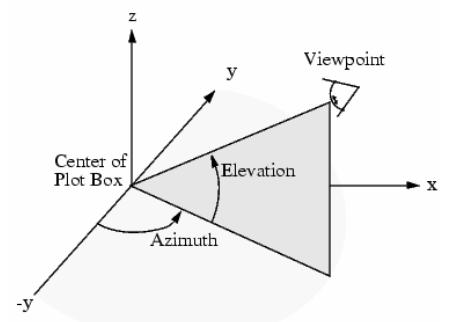
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσιάζονται οι βασικότερες μέθοδοι για την υλοποίηση της. Παρουσιάζεται η κεντρική προβολή, η παράλληλη προβολή και οι παραλλαγές τους. - Παράσταση επίπεδων καμπυλών
Μελετάται το πρόβλημα της παρεμβολής και της προσέγγισης. Παρουσιάζονται οι καλύτερες μέθοδοι παρεμβολής (Κυβικές Spline) καθώς και οι ακριβέστερες μέθοδοι προσέγγισης (Καμπύλες Bezier).
Το μάθημα έχει και εργαστηριακό κομμάτι (προαιρετικό).
Το περιεχόμενο του εργαστηρίου είναι:
- Μια εισαγωγή στη Matlab.
- Υλοποιούνται οι αλγόριθμοι που παρουσιάζονται στο μάθημα (είτε με την μορφή εργαστηριακών ασκήσεων, είτε απλά ως παραδείγματα).
- Παρουσιάζονται μερικές εφαρμογές της θεωρίας.
Τα θέματα τα οποία καλύπτονται στο μάθημα είναι:
- Αλγόριθμοι σχεδιασμού βασικών γεωμετρικών σχημάτων
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους. - Μετασχηματισμοί στο επίπεδο και στο χώρο των τριών διαστάσεων
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους. - Αλγόριθμοι αποκοπής καθώς και το πεδίο παράστασης (Viewport)
Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους. - Απεικονίσεις χώρου σε επίπεδο
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσ
Τα θέματα τα οποία καλύπτονται στο μάθημα είναι:
- Αλγόριθμοι σχεδιασμού βασικών γεωμετρικών σχημάτων
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους. - Μετασχηματισμοί στο επίπεδο και στο χώρο των τριών διαστάσεων
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους. - Αλγόριθμοι αποκοπής καθώς και το πεδίο παράστασης (Viewport)
Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους. - Απεικονίσεις χώρου σε επίπεδο
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσ
Περίγραμμα

Περιεχόμενο μαθήματος
Τα θέματα τα οποία καλύπτονται στο μάθημα είναι:
- Αλγόριθμοι σχεδιασμού βασικών γεωμετρικών σχημάτων
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους.
- Μετασχηματισμοί στο επίπεδο και στο χώρο των τριών διαστάσεων
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους.
- Αλγόριθμοι αποκοπής καθώς και το πεδίο παράστασης (Viewport)
Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους.
- Απεικονίσεις χώρου σε επίπεδο
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσιάζονται οι βασικότερες μέθοδοι για την υλοποίηση της. Παρουσιάζεται η κεντρική προβολή, η παράλληλη προβολή και οι παραλλαγές τους.
- Παράσταση επίπεδων καμπυλών
Μελετάται το πρόβλημα της παρεμβολής και της προσέγγισης. Παρουσιάζονται οι καλύτερες μέθοδοι παρεμβολής (Κυβικές Spline) καθώς και οι ακριβέστερες μέθοδοι προσέγγισης (Καμπύλες Bezier).
Διδάσκοντες

Μαριλένα Μητρούλη
Θέση: Αναπληρώτρια Καθηγήτρια
Ερευνητικά Ενδιαφέροντα: Αριθμητικά Θέματα στην Αλγεβρική Θεωρία Ελέγχου, Αριθμητική Γραμμική Αλγεβρα, Θεωρία Πινάκων, Ανάλυση Σφαλμάτων.
Προτεινόμενα συγγράμματα
Γραφικά: Αρχές και Αλγόριθμοι
Θ. Θεοχάρης, Α. Μπεμ
Εκδόσεις Συμμετρία
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Προαπαιτούμενα
Το μάθημα δεν έχει προαπαιτούμενα.
Σημειώματα Δικαιωμάτων Πνευματικής Ιδιοκτησίας
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Όνομα μέλους ή μελών ΔΕΠ, 2014. Μαριλένα Μητρούλη. Γραφικά με Ηλεκτρονικούς Υπολογιστές. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH124/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».
[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Σημείωμα Χρήσης Έργων Τρίτων
Οι σημειώσεις αποτελούν πνευματική ιδιοκτησία των συγγραφέων τους. Για χρήση τους σε έργο απαιτείται η λήψη άδειας χρήσης από αυτούς.
Η δομή και οργάνωση της παρουσίασης
Η δομή και οργάνωση της παρουσίασης, καθώς και το υπόλοιπο περιεχόμενο, αποτελούν πνευματική ιδιοκτησία της συγγραφέως και του Πανεπιστημίου Αθηνών και διατίθενται με άδεια Creative Commons Αναφορά Μη Εμπορική Χρήση Παρόμοια Διανομή Έκδοση 4.0 ή μεταγενέστερη.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
Τα θέματα τα οποία καλύπτονται στο μάθημα είναι:
- Αλγόριθμοι σχεδιασμού βασικών γεωμετρικών σχημάτων
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους. - Μετασχηματισμοί στο επίπεδο και στο χώρο των τριών διαστάσεων
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους. - Αλγόριθμοι αποκοπής καθώς και το πεδίο παράστασης (Viewport)
Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους. - Απεικονίσεις χώρου σε επίπεδο
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσιάζονται οι βασικότερες μέθοδοι για την υλοποίηση της. Παρουσιάζεται η κεντρική προβολή, η παράλληλη προβολή και οι παραλλαγές τους. - Παράσταση επίπεδων καμπυλών
Μελετάται το πρόβλημα της παρεμβολής και της προσέγγισης. Παρουσιάζονται οι καλύτερες μέθοδοι παρεμβολής (Κυβικές Spline) καθώς και οι ακριβέστερες μέθοδοι προσέγγισης (Καμπύλες Bezier).

Μαριλένα Μητρούλη
Θέση: Αναπληρώτρια Καθηγήτρια
Ερευνητικά Ενδιαφέροντα: Αριθμητικά Θέματα στην Αλγεβρική Θεωρία Ελέγχου, Αριθμητική Γραμμική Αλγεβρα, Θεωρία Πινάκων, Ανάλυση Σφαλμάτων.
Γραφικά: Αρχές και Αλγόριθμοι
Θ. Θεοχάρης, Α. Μπεμ
Εκδόσεις Συμμετρία
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Το μάθημα δεν έχει προαπαιτούμενα.
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Όνομα μέλους ή μελών ΔΕΠ, 2014. Μαριλένα Μητρούλη. Γραφικά με Ηλεκτρονικούς Υπολογιστές. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH124/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».

[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Σημείωμα Χρήσης Έργων Τρίτων
Οι σημειώσεις αποτελούν πνευματική ιδιοκτησία των συγγραφέων τους. Για χρήση τους σε έργο απαιτείται η λήψη άδειας χρήσης από αυτούς.
Η δομή και οργάνωση της παρουσίασης
Η δομή και οργάνωση της παρουσίασης, καθώς και το υπόλοιπο περιεχόμενο, αποτελούν πνευματική ιδιοκτησία της συγγραφέως και του Πανεπιστημίου Αθηνών και διατίθενται με άδεια Creative Commons Αναφορά Μη Εμπορική Χρήση Παρόμοια Διανομή Έκδοση 4.0 ή μεταγενέστερη.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Σημαντικοί Σταθμοί
- Εφαρμογές
- Τεχνολογία (Συσκευές Εισόδου / Εξόδου)
Λέξεις Κλειδιά: συσκευές εισόδου, ποντίκι, πληκτρολόγιο, συσκευές εξόδου, διανυσματική οθόνη, πλεγματική οθόνη, διανυσματικοί εκτυπωτές, πλεγματικοί εκτυπωτές
Σχεδιασμός ευθείας, κύκλου, έλλειψης στηριζόμενοι στις γεωμετρικές εξισώσεις τους και στην τεχνική του Bresenham. Γίνεται αναλυτική σύγκριση των μεθόδων όσον αφορά την αποτελεσματικότητα τους.
Λέξεις Κλειδιά: ευθύγραμμο τμήμα, κύκλος, έλλειψη, αλγόριθμος Bresenham, RasterOp
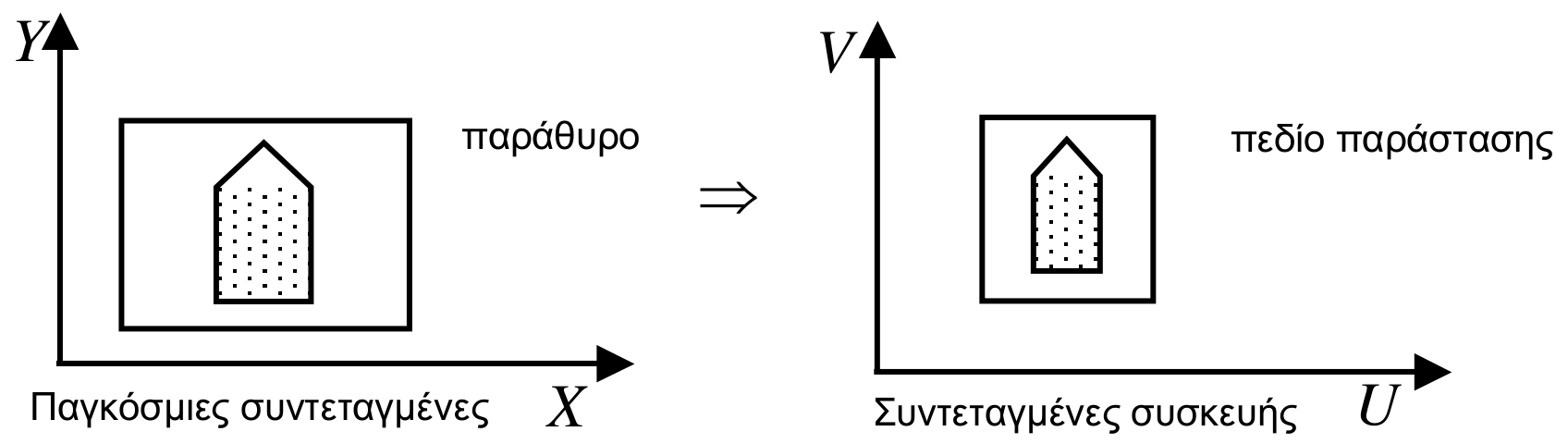
Γεωμετρικοί μετασχηματισμοί και μετασχηματισμοί αξόνων. Παρουσιάζονται οι βασικοί πίνακες μετασχηματισμού που εκτελούν μεταφορά, στροφή, scaling και συμμετρία ως προς άξονες και εξετάζονται οι εφαρμογές τους.
Λέξεις Κλειδιά: γεωμετρικοί μετασχηματισμοί, μετασχηματισμοί αξόνων, συσχετισμένοι μετασχηματισμοί, μεταφορά, στροφή, στρέβλωση, αλλάγη κλίμακας

Εξετάζεται το πρόβλημα της αποκοπής γεωμετρικού σχήματος, ως προς συγκεκριμένο παράθυρο (viewport). Παρουσιάζονται οι ακόλουθοι αλγόριθμοι: Αλγόριθμος του Μέσου, Αλγόριθμος Cohen - Sutherland, Αλγόριθμος Liang - Barsky. Γίνεται σύγκριση των αλγορίθμων αυτών ως προς την αποτελεσματικότητά τους.
Λέξεις Κλειδιά: αποκοπή, αλγόριθμος μέσου, αλγόριθμος Cohen - Sutherland, αλγόριθμος Liang - Barsky, αλγόριθμος Sutherland - Hodgman, αλγόριθμος Greiner - Hormann
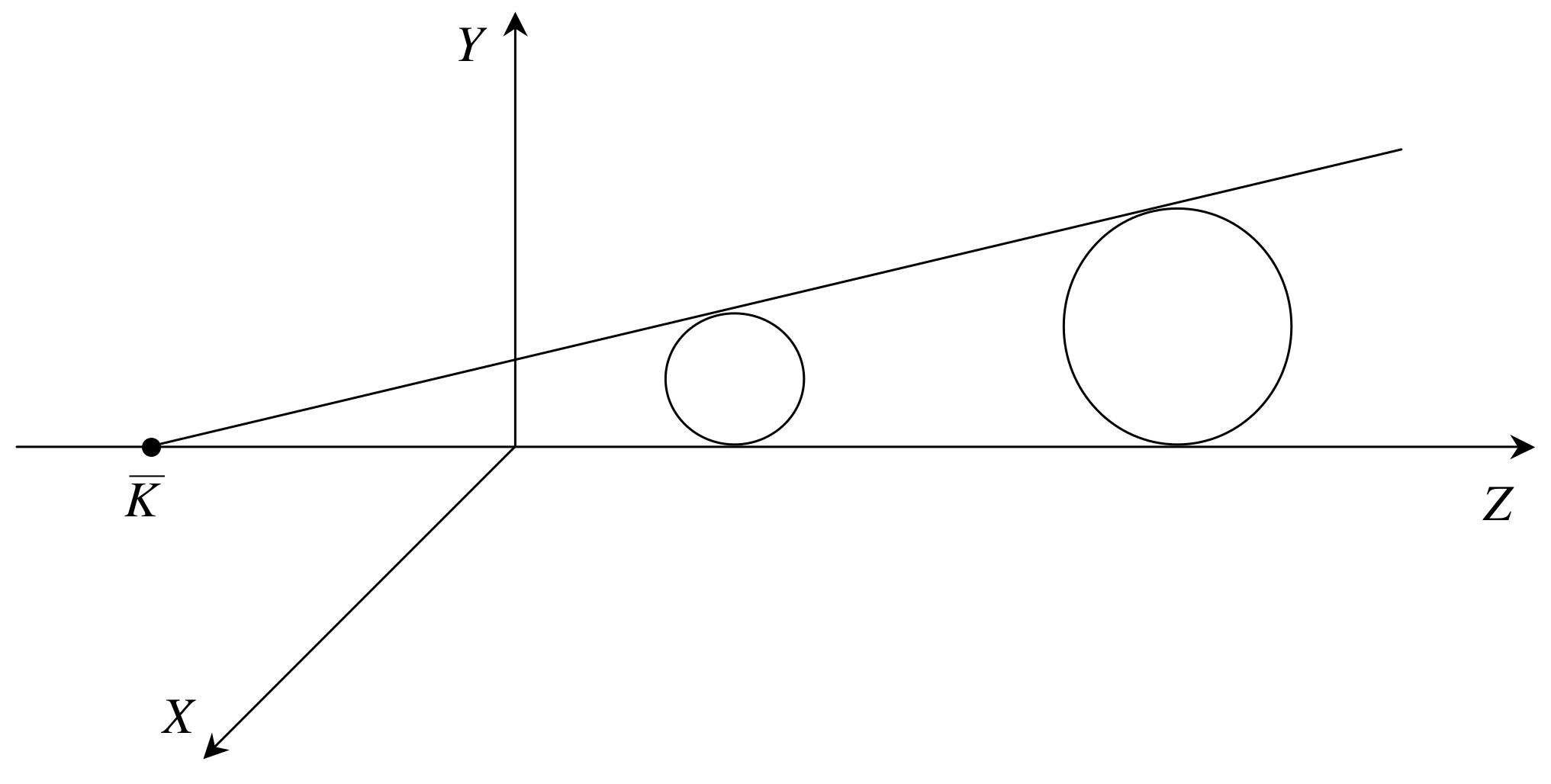
Εξετάζεται εκτενώς το πρόβλημα της προβολής και παρουσιάζονται οι βασικότερες μέθοδοι για την υλοποίηση της. Παρουσιάζεται η κεντρική προβολή, η παράλληλη προβολή και οι παραλλαγές τους.
Λέξεις Κλειδιά: προβολές, προοπτική προβολή, παράλληλη προβολή, πλάγια παράλληλη προβολή, μετασχηματισμός παρατήρησης
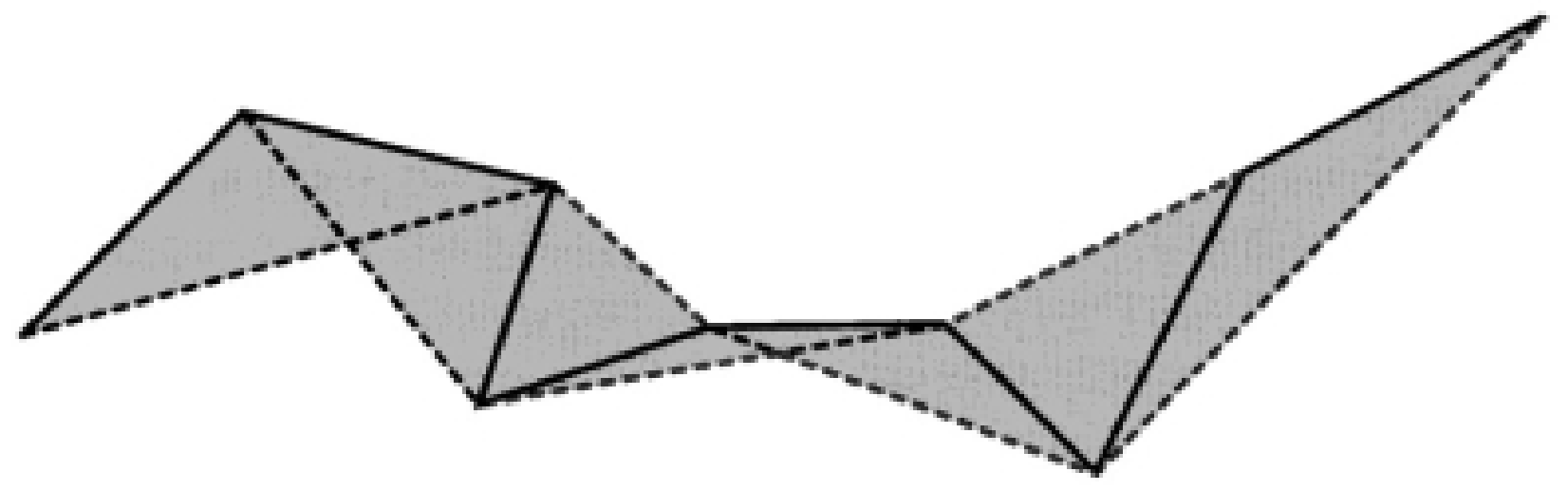
Μελετάται το πρόβλημα της παρεμβολής και της προσέγγισης. Παρουσιάζονται οι καλύτερες μέθοδοι παρεμβολής (Κυβικές Spline) καθώς και οι ακριβέστερες μέθοδοι προσέγγισης (Καμπύλες Bezier).
Λέξεις Κλειδιά: καμπύλες Bézier, πολυώνυμα Bernstein, καμπύλες B-Spline, καμπύλες παρεμβολής, αλγόριθμος Aitken, παρεμβολή Hermite
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -