Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση
Δημήτρης Χασάπης
Στο μάθημα παρουσιάζονται οι βασικές διακρίσεις του χώρου και οι δυσκολίες που συναντούν τα παιδιά της προσχολικής ηλικίας στην ιδιοποίηση τους και στην ανάπτυξη ικανοτήτων χειρισμού χωρικών σχέσεων και γεωμετρικών εννοιών στις δραστηριότητες της καθημερινότητας τους. Στη βάση αυτή παρουσιάζονται και συζητούνται μέθοδοι και τεχνικές διδασκαλίας τους στην προσχολική εκπαίδευση.
Λιγότερα
Στο μάθημα παρουσιάζονται οι βασικές διακρίσεις του χώρου και οι δυσκολίες που συναντούν τα παιδιά της προσχολικής ηλικίας στην ιδιοποίηση τους και στην ανάπτυξη ικανοτήτων χειρισμού χωρικών σχέσεων και γεωμετρικών εννοιών στις δραστηριότητες της καθημερινότητας τους. Στη βάση αυτή παρουσιάζονται και συζητούνται μέθοδοι και τεχνικές διδασκαλίας τους στην προσχολική εκπαίδευση.
Στο μάθημα παρουσιάζονται οι βασικές διακρίσεις του χώρου και οι δυσκολίες που συναντούν τα παιδιά της προσχολικής ηλικίας στην ιδιοποίηση τους και στην ανάπτυξη ικανοτήτων χειρισμού χωρικών σχέσεων και γεωμετρικών εννοιών στις δραστηριότητες της καθημερινότητας τους. Στη βάση αυτή παρουσιάζονται και συζητούνται μέθοδοι και τεχνικές διδασκαλίας τους στην προσχολική εκπαίδευση.
Περίγραμμα

Περιεχόμενο μαθήματος
- Η αίσθηση, η αντίληψη και η νόηση του χώρου.
- Η νοητική αναπαράσταση του χώρου.
- Τοπολογικές και προβολικές σχέσεις στο χώρο.
- Ευκλείδειος χώρος και γεωμετρικές έννοιες.
- Σχέσεις ευθειών στο χώρο (κάθετες και παράλληλες ευθείες, γωνίες).
- Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων.
- Κανονικότητες, συμμετρίες και μετασχηματισμοί στο χώρο.
- Η κατανόηση των γεωμετρικών εννοιών από τα παιδιά και η ανάπτυξη της χωρικής και γεωμετρικής σκέψης.
- Η οπτικοποιημένη σκέψη.
Προαπαιτούμενα
514: Βασικές έννοιες μαθηματικών
Βιβλιογραφία
- Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους, Ζαχάρος Κώστας, ISBN: 978-960-455-128-6
- Τα μαθηματικά των παιδιών 4-6 ετών, Καφούση Σόνια, Σκουμπουρδή Χρυσάνθη, ISBN: 978-960-16-2677-2
Προτεινόμενα συγγράμματα
- Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους, Ζαχάρος Κώστας, ISBN: 978-960-455-128-6
- Τα μαθηματικά των παιδιών 4-6 ετών, Καφούση Σόνια,Σκουμπουρδή Χρυσάνθη, ISBN: 978-960-16-2677-2
Βιογραφικό - Δημήτριος Χασάπης
ΣΠΟΥΔΕΣ
- 1992 Διδακτορικό Δίπλωμα στις Επιστήμες της Αγωγής, Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Πανεπιστημίου Πάτρας.
- 1979 Δίπλωμα Παιδαγωγικής Επιμόρφωσης στην Παιδαγωγική Σχολή της Σχολής Εκπαιδευτικών Λειτουργών Επαγγελματικής & Τεχνικής Εκπαίδευσης.
- 1978 Μεταπτυχιακό Δίπλωμα Master of Science in Mathematics, The City University, London. Τίτλος μεταπτυχιακής εργασίας "Existence and Uniqueness Theorems to Initial Value Problems for Ordinary and Partial Differential Equations".
- 1972 Πτυχίου του Μαθηματικού Τμήματος του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης
ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑ
- 1976 – 1994 ΟΡΓΑΝΙΣΜΟΣ ΑΠΑΣΧΟΛΗΣΗΣ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ (ΟΑΕΔ), ως εκπαιδευτικός στις Σχολές Επαγγελματικής Κατάρτισης και ως υπεύθυνος ανάπτυξης, εφαρμογής και αξιολόγησης προγραμμάτων αρχικής και συνεχιζόμενης επαγγελματικής κατάρτισης της Διεύθυνσης Επαγγελματικής Εκπαίδευσης της Διοίκησης του ΟΑΕΔ.
- Την ίδια χρονική περίοδο επιστημονική δραστηριότητα και αντίστοιχο ερευνητικό έργο στο αντικείμενο της Επαγγελματικής Εκπαίδευσης & Κατάρτισης στα πλαίσια αντίστοιχων Εθνικών και Ευρωπαϊκών φορέων (Εθνικό Ινστιτούτο Εργασίας, Ινστιτούτο Εργασίας ΓΣΕΕ, CEDEFOP, Ευρωπαϊκό Πρόγραμμα Leonardo, ADAPT κ.α.)
- 1989 - 1994 ΣΧΟΛΗ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΛΕΙΤΟΥΡΓΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ (ΣΕΛΕΤΕ), ως Έκτακτος Καθηγητής.
- 1994 – 2008 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ, ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ, Λέκτορας στο γνωστικό αντικείμενο «Διδακτική των Μαθηματικών» και από το 1998 Επίκουρος Καθηγητής στο γνωστικό αντικείμενο «Μαθηματική Εκπαίδευση».
- 2008 μέχρι σήμερα ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ Επίκουρος Καθηγητής και από το 2009 Αναπληρωτής Καθηγητής στο γνωστικό αντικείμενο «Μαθηματική Εκπαίδευση» (ΦΕΚ 459/17.6.2009).
- 2005 μέχρι σήμερα ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ, Μεταπτυχιακό Πρόγραμμα «Σπουδές στην Εκπαίδευση - Εκπαίδευση Ενηλίκων» Καθηγητής-Σύμβουλος στη διδασκαλία της Θεματικής Ενότητας «Ανάπτυξη και Αξιολόγηση Εκπαιδευτικών Προγραμμάτων».
- Η αίσθηση, η αντίληψη και η νόηση του χώρου.
- Η νοητική αναπαράσταση του χώρου.
- Τοπολογικές και προβολικές σχέσεις στο χώρο.
- Ευκλείδειος χώρος και γεωμετρικές έννοιες.
- Σχέσεις ευθειών στο χώρο (κάθετες και παράλληλες ευθείες, γωνίες).
- Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων.
- Κανονικότητες, συμμετρίες και μετασχηματισμοί στο χώρο.
- Η κατανόηση των γεωμετρικών εννοιών από τα παιδιά και η ανάπτυξη της χωρικής και γεωμετρικής σκέψης.
- Η οπτικοποιημένη σκέψη.
514: Βασικές έννοιες μαθηματικών
- Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους, Ζαχάρος Κώστας, ISBN: 978-960-455-128-6
- Τα μαθηματικά των παιδιών 4-6 ετών, Καφούση Σόνια, Σκουμπουρδή Χρυσάνθη, ISBN: 978-960-16-2677-2
- Οι μαθηματικές έννοιες στην προσχολική εκπαίδευση και η διδασκαλία τους, Ζαχάρος Κώστας, ISBN: 978-960-455-128-6
- Τα μαθηματικά των παιδιών 4-6 ετών, Καφούση Σόνια,Σκουμπουρδή Χρυσάνθη, ISBN: 978-960-16-2677-2
ΣΠΟΥΔΕΣ
- 1992 Διδακτορικό Δίπλωμα στις Επιστήμες της Αγωγής, Παιδαγωγικό Τμήμα Δημοτικής Εκπαίδευσης Πανεπιστημίου Πάτρας.
- 1979 Δίπλωμα Παιδαγωγικής Επιμόρφωσης στην Παιδαγωγική Σχολή της Σχολής Εκπαιδευτικών Λειτουργών Επαγγελματικής & Τεχνικής Εκπαίδευσης.
- 1978 Μεταπτυχιακό Δίπλωμα Master of Science in Mathematics, The City University, London. Τίτλος μεταπτυχιακής εργασίας "Existence and Uniqueness Theorems to Initial Value Problems for Ordinary and Partial Differential Equations".
- 1972 Πτυχίου του Μαθηματικού Τμήματος του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης
ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΔΡΑΣΤΗΡΙΟΤΗΤΑ
- 1976 – 1994 ΟΡΓΑΝΙΣΜΟΣ ΑΠΑΣΧΟΛΗΣΗΣ ΕΡΓΑΤΙΚΟΥ ΔΥΝΑΜΙΚΟΥ (ΟΑΕΔ), ως εκπαιδευτικός στις Σχολές Επαγγελματικής Κατάρτισης και ως υπεύθυνος ανάπτυξης, εφαρμογής και αξιολόγησης προγραμμάτων αρχικής και συνεχιζόμενης επαγγελματικής κατάρτισης της Διεύθυνσης Επαγγελματικής Εκπαίδευσης της Διοίκησης του ΟΑΕΔ.
- Την ίδια χρονική περίοδο επιστημονική δραστηριότητα και αντίστοιχο ερευνητικό έργο στο αντικείμενο της Επαγγελματικής Εκπαίδευσης & Κατάρτισης στα πλαίσια αντίστοιχων Εθνικών και Ευρωπαϊκών φορέων (Εθνικό Ινστιτούτο Εργασίας, Ινστιτούτο Εργασίας ΓΣΕΕ, CEDEFOP, Ευρωπαϊκό Πρόγραμμα Leonardo, ADAPT κ.α.)
- 1989 - 1994 ΣΧΟΛΗ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΛΕΙΤΟΥΡΓΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ (ΣΕΛΕΤΕ), ως Έκτακτος Καθηγητής.
- 1994 – 2008 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ, ΠΑΙΔΑΓΩΓΙΚΟ ΤΜΗΜΑ ΔΗΜΟΤΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ, Λέκτορας στο γνωστικό αντικείμενο «Διδακτική των Μαθηματικών» και από το 1998 Επίκουρος Καθηγητής στο γνωστικό αντικείμενο «Μαθηματική Εκπαίδευση».
- 2008 μέχρι σήμερα ΕΘΝΙΚΟ & ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ Επίκουρος Καθηγητής και από το 2009 Αναπληρωτής Καθηγητής στο γνωστικό αντικείμενο «Μαθηματική Εκπαίδευση» (ΦΕΚ 459/17.6.2009).
- 2005 μέχρι σήμερα ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ, Μεταπτυχιακό Πρόγραμμα «Σπουδές στην Εκπαίδευση - Εκπαίδευση Ενηλίκων» Καθηγητής-Σύμβουλος στη διδασκαλία της Θεματικής Ενότητας «Ανάπτυξη και Αξιολόγηση Εκπαιδευτικών Προγραμμάτων».
Στην παρούσα ενότητα εξετάζονται α) τα χαρακτηριστικά του χώρου για το παιδί, β) η αίσθηση, η αντίληψη και η νόηση του χώρου, γ) οι ικανότητες αντίληψης του χώρου, και δ) η νοητική πρόσληψη του χώρου.
Περιεχόμενα ενότητας
- Όραση, αφή, ακοή
- Ποιά τα χαρακτηριστικά του χώρου για ένα παιδί μέχρι 2 ετών;
- Η αντίληψη της τρίτης διάστασης είναι εγγενής ή επίκτητη;
- Ικανότητες που δομούν την αίσθηση του χώρου
- Η μονιμότητα των αντικειμένων και η σταθερότητα των χαρακτηριστικών τους στο χώρο
- Η απόδοση νοήματος στις οπτικές εμπειρίες (οπτική αντίληψη)
Περιγραφή ενότητας
Στην παρούσα ενότητα εξετάζονται α) η διάκριση των χωρικών σχέσεων: Τοπολογικές προβολικές και γεωμετρικές σχέσεις στο χώρο, β) η έννοια της γραμμικότητας και η ευθεία γραμμή στο χώρο.
Περιεχόμενα ενότητας
- Σε ποιες κατηγορίες διακρίνονται οι χωρικές σχέσεις;
- Τοπολογικές σχέσεις
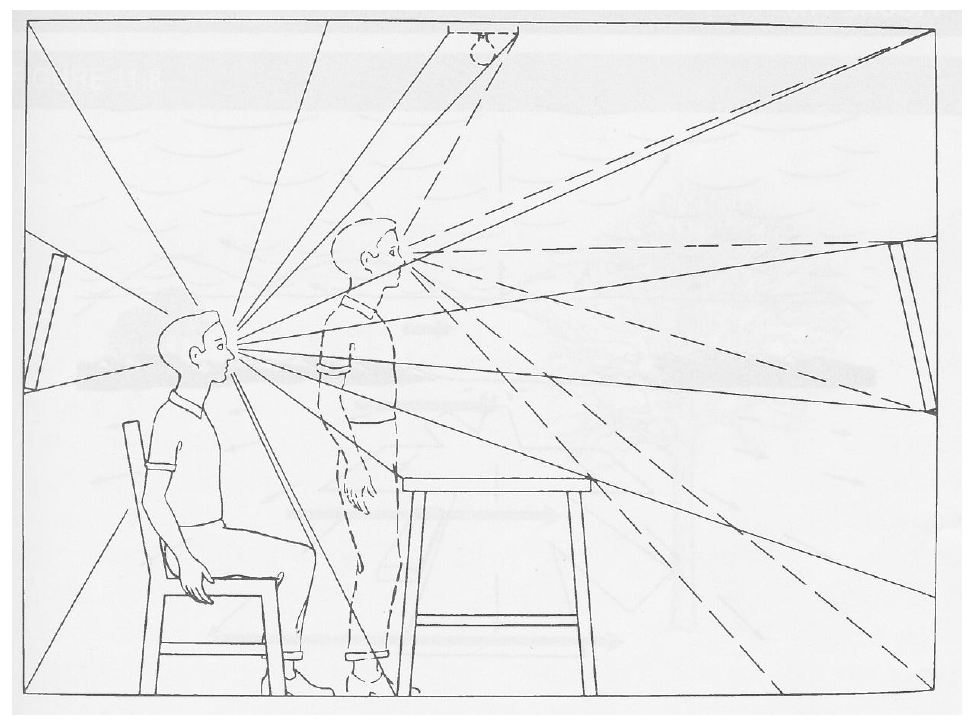
- Προβολικές σχέσεις
- Κεντρική προβολή
- Παράλληλη προβολή
- Προβολικές σχέσεις
- Η έννοια της ευθείας γραμμής
- Τι λέμε προβολική ευθεία
Περιγραφή ενότητας
Στην παρούσα ενότητα παρουσιάζεται η θεωρία των van Hiele και τα επίπεδα συγκρότησης και ανάπτυξης της γεωμετρικής σκέψης, σύμφωνα με αυτήν.
Περιεχόμενα ενότητας
- Dina και Pierre Van Hiele
- Επίπεδα συγκρότησης και ανάπτυξης της γεωμετρικής σχέσης
0 – προ-αναγνώριση
1 - Οπτική θεώρηση / Αναγνώριση
2 - Περιγραφική θεώρηση / Ανάλυση
3 – Σχεσιακή θεώρηση / Διάταξη – ταξινόμηση ιδιοτήτων
4 – Τυπική παραγωγική θεώρηση / Απόδειξη
5 – Λογική αυστηρότητα
- Ιδιότητες των επιπέδων Van Hiele
- Διδακτικές παρεμβάσεις για την ενίσχυση της μετάβασης από το ένα επίπεδο σε άλλο σε φάσεις
1η Φάση: Διερεύνηση
2η Φάση: Κατευθυνόμενος προσανατολισμός
3η Φάση: Ερμηνεία – επεξήγηση
4η Φάση: Ελεύθερος προσανατολισμός
5η Φάση: Ολοκλήρωση
Περιγραφή ενότητας
Στην παρούσα ενότητα εξετάζονται η μετρική θεώρηση του χώρου και συγκεκριμένα η απόσταση ανάμεσα σε δύο σημεία / το μήκος, β) τα επίπεδα σχήματα /το εμβαδόν, γ) τα στερεά σχήματα / όγκος.
Περιεχόμενα ενότητας
Οι γεωμετρικές σχέσεις – μετρική θεώρηση του χώρου.
- Οι βασικές έννοιες της γεωμετρίας: σημείο, γραμμή, επίπεδο, γωνία, ευθύγραμμα σχήματα, κύκλος
- Σχέσεις επίπεδων σχημάτων: ίσα σχήματα, όμοια σχήματα
Απόσταση ανάμεσα σε δύο σημεία / μήκος.
- Σημείο, γραμμή.
- Ποιες οι σχέσεις σημείων και ευθείας;
- H διάκριση απόστασης και μήκους
- Η μέτρηση γενικά
- Μέτρηση μήκους
- Η γωνία και η μέτρησή της
Επιφάνεια / επίπεδα σχήματα / εμβαδόν
- Μέτρηση μίας επιφάνειας, σύγκριση ομοειδών μεγεθών, χρήση αυθαίρετων μονάδων.
- Διατήρηση της έκτασης μίας επιφάνειας
- Μέτρηση με μονάδα μέτρησης
- Μέτρηση με χρήση γραμμικών μέτρων
- Χρήση τυπικών μονάδων μέτρησης
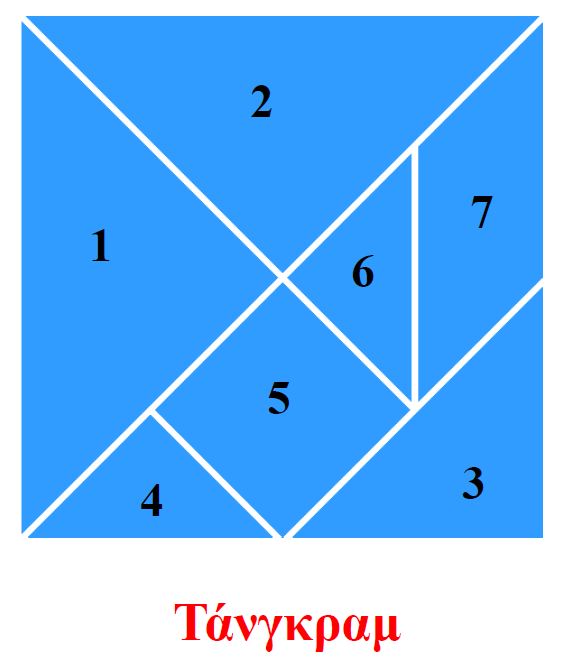
- Τάνγκραμ
- Τετράγωνος γεωπίνακας
Χώρος / στερεά σχήματα / όγκος
- Διάκριση χωρητικότητας και όγκου
- Μάζα
- Διατήρηση όγκου
- Η διατήρηση του όγκου ως χωρητικότητας
Περιγραφή ενότητας
Στην παρούσα ενότητα παρουσιάζονται α) οι κανόνες μετατόπισης των γεωμετρικών σχημάτων σε ένα επίπεδο ώστε κάποια ιδιότητα των σχημάτων να παραμένει αναλλοίωτη, β) Μετατόπιση, περιστροφή, ανάκλαση, μεγέθυνση.
Περιεχόμενα ενότητας
- Μετατόπιση
- Περιστροφή
- Συμμετρία ως προς σημείο
- Κεντρική συμμετρία
- Ανάκλαση
- Ανάκλαση – συμμετρία ως προς άξονα
- Μεγέθυνση
- Δραστηριότητες
 Περιγραφή ενότητας
Περιγραφή ενότητας
Στην παρούσα ενότητα εξετάζονται α) η τοποθέτηση και προσανατολισμός στο χώρο. β) η νοητική παράσταση και αναπαράσταση του χώρου, και γ) το παιδικό σχέδιο.
Περιεχόμενα ενότητας
- Toποθέτηση και προσανατολισμός στο χώρο
- Το ανθρώπινο σώμα ως σύστημα αναφοράς
- Προτεινόμενες ασθησιο-κινητικές δραστηριότητες
- Διάκριση των χωρικών σχέσεων
- Τοπολογικές σχέσεις
Περιγραφή ενότητας
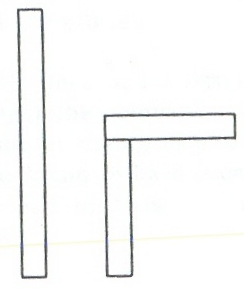
Στην παρούσα ενότητα εξετάζονται α) η μετάβαση στη μετρική θεώρηση του χώρου, β) η κατανόηση των εννοιών των παράλληλων γραμμών, της ομοιότητας των σχημάτων και των οριζόντιων και κατακόρυφων / κάθετων γραμμών γ) η διατήρηση του μήκους.
Περιεχόμενα ενότητας
- Ποιες είναι οι νοητικές προϋποθέσεις για τη συγκρότηση των προβολικών σχέσεων;
- H μετάβαση από την προβολική στη μετρική θεώρηση του χώρου
- Παράλληλες γραμμές
- Ομοιότητα
- Οι γεωμετρικές σχέσεις
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -