Πιθανότητες και Στατιστική
Αντώνιος Οικονόμου
Το αντικείμενο του μαθήματος Πιθανότητες και Στατιστική είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα.
Η ανάπτυξη της πιθανοθεωρητικής σκέψης είναι ένα από τα θεμελιώδη εφόδια που πρέπει να παρέχει μια σύγχρονη επιστημονική παιδεία. Η σημασία της έχει πλέον αναγνωριστεί σε μια ποικιλία πεδίων. Πράγματι, πέρα από τις κλασικές εφαρμογές της στα πλαίσια των θετικών επιστημών, η πιθανοθεωρητική σκέψη είναι θεμελιώδης για τη λήψη αποφάσεων στο χώρο των επιστημών υγείας, στην αποτίμηση κινδύνων στο χώρο της οικονομικής επιστήμης και της αναλογιστικής κ.α. Επίσης, αποτελεί το προαπαιτούμενο και θεμέλιο της Στατιστικής που χρησιμοποιείται ευρύτατα για τη συναγωγή συμπερασμάτων στις θετικές, κοινωνικές, οικονομικές επιστήμες, όπως και στη βιολογία και στην ιατρική.
Το μάθημα Πιθανότητες και Στατιστική εισάγει τους φοιτητές στα βασικά πιθανοθεωρητικά μοντέλα και υπολογιστικά εργαλεία, συνδυάζοντας τη μαθηματική προσέγγιση με την εννοιολογική και διαισθητική κατανόηση. Επιπλέον περιλαμβάνει μια σύντομη εισαγωγή στην Κλασική Στατιστική Συμπερασματολογία, αναπτύσοντας θέματα εκτιμητικής, διαστημάτων εμπιστοσύνης και ελέγχων υποθέσεων.
Το μάθημα απευθύνεται στους δευτεροετείς φοιτητές του Τμήματος Πληροφορικής και Τηλεπικοινωνιών του Πανεπιστημίου Αθηνών. Γενικότερα θα μπορούσε να γίνει κατανοητό από φοιτητές τμημάτων Μαθηματικών, Στατιστικής, Φυσικών Επιστημών και Πολυτεχνικών Σχολών που έχουν ένα βασικό υπόβαθρο στον Απειροστικό Λογισμό.
ΛιγότεραΤο αντικείμενο του μαθήματος Πιθανότητες και Στατιστική είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα.
Η ανάπτυξη της πιθανοθεωρητικής σκέψης είναι ένα από τα θεμελιώδη εφόδια που πρέπει να παρέχει μια σύγχρονη επιστημονική παιδεία. Η σημασία της έχει πλέον αναγνωριστεί σε μια ποικιλία πεδίων. Πράγματι, πέρα από τις κλασικές εφαρμογές της στα πλαίσια των θετικών επιστημών, η πιθανοθεωρητική σκέψη είναι θεμελιώδης για τη λήψη αποφάσεων στο χώρο των επιστημών υγείας, στην αποτίμηση κινδύνων στο χώρο της οικονομικής επιστήμης και της αναλογιστικής κ.α. Επίσης, αποτελεί το προαπαιτούμενο και θεμέλιο της Στατιστικής που χρησιμοποιείται ευρύτατα για τη συναγωγή συμπερασμάτων στις θετικές, κοινωνικές, οικονομικές επιστήμες, όπως και στη βιολογία και στην ιατρική.
Το μάθημα Πιθανότητες και Στατιστική εισάγει τους φοιτητές στα βασικά πιθανοθεωρητικά μοντέλα και υπολογιστικά εργαλεία, συνδυάζοντας τη μαθηματική π
Το αντικείμενο του μαθήματος Πιθανότητες και Στατιστική είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα.
Η ανάπτυξη της πιθανοθεωρητικής σκέψης είναι ένα από τα θεμελιώδη εφόδια που πρέπει να παρέχει μια σύγχρονη επιστημονική παιδεία. Η σημασία της έχει πλέον αναγνωριστεί σε μια ποικιλία πεδίων. Πράγματι, πέρα από τις κλασικές εφαρμογές της στα πλαίσια των θετικών επιστημών, η πιθανοθεωρητική σκέψη είναι θεμελιώδης για τη λήψη αποφάσεων στο χώρο των επιστημών υγείας, στην αποτίμηση κινδύνων στο χώρο της οικονομικής επιστήμης και της αναλογιστικής κ.α. Επίσης, αποτελεί το προαπαιτούμενο και θεμέλιο της Στατιστικής που χρησιμοποιείται ευρύτατα για τη συναγωγή συμπερασμάτων στις θετικές, κοινωνικές, οικονομικές επιστήμες, όπως και στη βιολογία και στην ιατρική.
Το μάθημα Πιθανότητες και Στατιστική εισάγει τους φοιτητές στα βασικά πιθανοθεωρητικά μοντέλα και υπολογιστικά εργαλεία, συνδυάζοντας τη μαθηματική π
Περίγραμμα

Ομάδα στόχος
Προπτυχιακοί φοιτητές Τμημάτων Πληροφορικής και Επικοινωνιών και γενικότερα Θετικών Επιστημών και Πολυτεχνικών Σχολών
Περιεχόμενο μαθήματος
Το μάθημα στοχεύει στην ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα. Επίσης περιλαμβάνει μια εισαγωγή στην κλασική στατιστική συμπερασματολογία. Η δομή του έχει ως εξής:
- Δειγματικός χώρος και ενδεχόμενα. Αξιωματική θεμελίωση της Θεωρίας Πιθανοτήτων.
- Δεσμευμένη πιθανότητα.
- Θεώρημα ολικής πιθανότητας και κανόνας του Bayes.
- Ανεξαρτησία.
- Βασικές αρχές απαρίθμησης. Πεπερασμένοι δειγματικοί χώροι και κλασική πιθανότητα.
- Διακριτές τυχαίες μεταβλητές: Συνάρτηση (μάζας) πιθανότητας, μέση τιμή και διασπορά.
- Πολυδιάστατες διακριτές τυχαίες μεταβλητές: Από κοινού συνάρτηση (μάζας) πιθανότητας, δέσμευση, ανεξαρτησία.
- Συνεχείς τυχαίες μεταβλητές: Συνάρτηση πυκνότητας πιθανότητας, μέση τιμή και διασπορά.
- Πολυδιάστατες συνεχείς τυχαίες μεταβλητές: Από κοινού συνάρτηση πυκνότητας πιθανότητας, δέσμευση, ανεξαρτησία.
- Κατανομές συναρτήσεων τυχαίων μεταβλητών.
- Συνδιακύμανση (συνδιασπορά) και συσχέτιση.
- Δεσμευμένη μέση τιμή και διασπορά.
- Νόμος των Μεγάλων Αριθμών και Κεντρικό Οριακό Θεώρημα.
- Εισαγωγή στην κλασική στατιστική συμπερασματολογία.
- Εισαγωγή στην εκτιμητική και στα διαστήματα εμπιστοσύνης.
- Γραμμική παλινδρόμηση
- Εισαγωγή στους Ελέγχους υποθέσεων.
Μαθησιακοί στόχοι
Σκοπός του μαθήματος είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα. Επίσης η κατανόηση βασικών τεχνικών για τη στατιστική ανάλυση δεδομένων.
Στο τέλος του μαθήματος ο εκπαιδευόμενος-φοιτητής θα πρέπει να είναι σε θέση:
- να μοντελοποιεί διαδικασίες και καταστάσεις που εμφανίζονται στην καθημερινή πραγματικότητα ή σε άλλες επιστημονικές περιοχές στο πλαίσιο της Θεωρίας Πιθανοτήτων
- να κατανοεί τις βασικές έννοιες της Θεωρίας Πιθανοτήτων, όπως την έννοια του δειγματικού σημείου, του δειγματικού χώρου, του ενδεχομένου, της πιθανότητας, της δεσμευμένης πιθανότητας, της τυχαίας μεταβλητής κλπ.
- να μπορεί να κάνει βασικούς υπολογισμούς πιθανοτήτων, μέσων τιμών, διασπορών κλπ. σε προβλήματα που εμπεριέχουν τυχαιότητα.
- να χρησιμοποιεί επιχειρήματα δέσμευσης για τους υπολογισμούς πιθανοτήτων, μέσων τιμών, διασπορών κλπ. σε προβλήματα που εμπεριέχουν τυχαιότητα
- να αντιλαμβάνεται διαισθητικά τα βασικά οριακά θεωρήματα της Θεωρίας Πιθανοτήτων (νόμοι των μεγάλων αριθμών, κεντρικό οριακό θεώρημα) και να μπορεί να τα χρησιμοποιεί σε προσεγγιστικούς υπολογισμούς πιθανοτήτων.
- να μπορεί να πραγματοποιεί απλές στατιστικές αναλύσεις δεδομένων, χρησιμοποιώντας βασικές τεχνικές από την εκτιμητική, τα διαστήματα εμπιστοσύνης και τους ελέγχους υποθέσεων.
Προτεινόμενα συγγράμματα
Ελληνικά:
- Μπερτσεκά, Δ. και Τσιτσικλή, Γ. (2013) Εισαγωγή στις Πιθανότητες με Στοιχεία Στατιστικής. Εκδόσεις Τζιόλα, Θεσσαλονίκη.
- Δαμιανού, Χ.Χ., Παπαδάτου, Ν.Δ. και Χαραλαμπίδη, Χ.Α.(2010) Εισαγωγή στις Πιθανότητες και τη Στατιστική. Εκδόσεις Συμμετρία, Αθήνα
Αγγλικά:
- Bertsekas, D.P. and Tsitsiklis J. (2008) J. Introduction to Probability -2nd Edition, Athena Scientific.
- Walpole, R.E., Myers, R.H., Myers, S.L. and Ye, K. (2007) Probability and Statistics for Engineers and Scientists, Pearson
Μέθοδοι διδασκαλίας
Διδασκαλία καθ΄ έδρας και συμπληρωματική-ενισχυτική εκπαίδευση μέσω ασύγχρονης πλατφόρμας – Ασκήσεις.
Προαπαιτούμενα
Είναι απαραίτητη η προγενέστερη επαφή του φοιτητή με τις βασικές έννοιες και τεχνικές Απειροστικού Λογισμού μιας και πολλών μεταβλητών. Ειδικότερα υπολογιστικά θέματα όπως υπολογισμοί ολοκληρωμάτων και αθροισμάτων θα πρέπει να είναι οικεία στους φοιτητές. Η επαφή με κάποιο μάθημα Διακριτών Μαθηματικών, αν και όχι απαραίτητη, είναι επιθυμητή.
Βιβλιογραφία
Συγγράμματα:
- Μπερτσεκάς, Δ. και Τσιτσικλής, Γ. (2013) Εισαγωγή στις Πιθανότητες με Στοιχεία Στατιστικής. Εκδόσεις Τζιόλα, Θεσσαλονίκη.
- Δαμιανού, Χ.Χ., Παπαδάτου, Ν.Δ. και Χαραλαμπίδη, Χ.Α.(2010) Εισαγωγή στις Πιθανότητες και τη Στατιστική. Εκδόσεις Συμμετρία, Αθήνα.
- Walpole, R.E., Myers, R.H., Myers, S.L. and Ye, K. (2007) Probability and Statistics for Engineers and Scientists, Pearson. (In English).
Πηγές στο Διαδίκτυο:
Άλλα σχετικά ανοικτά μαθήματα άλλων ιδρυμάτων εσωτερικού ή εξωτερικού:
- Probabilistic Systems Analysis and Applied Probability MITOpenCourseware: http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-041-probabilistic-systems-analysis-and-applied-probability-fall-2010/index.htm
Διδάσκοντες
 Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Σπουδές: Πτυχίο Μαθηματικών Πανεπιστημίου Αθηνών (1993), Μεταπτυχιακό στα Θεωρητικά Μαθηματικά UCLA (1994), Μεταπτυχιακό στη Στατιστική και Επιχειρησιακή Έρευνα Πανεπιστημίου Αθηνών (1997) και Διδακτορικό στα Μαθηματικά Πανεπιστημίου Αθηνών (1998). Ερευνητικά ενδιαφέροντα: Πιθανότητες, Επιχειρησιακή Έρευνα, Μαθηματική Βιολογία. Ειδικότερα, προβλήματα υπολογισμών, στοχαστικών συγκρίσεων και βελτιστοποίησης σε στοχαστικές διαδικασίες με εφαρμογές στη θεωρία συστημάτων εξυπηρέτησης (θεωρία ουρών) και στα στοχαστικά πρότυπα εξέλιξης πληθυσμών.
http://users.uoa.gr/~aeconom/CVpdf.pdf
Προπτυχιακοί φοιτητές Τμημάτων Πληροφορικής και Επικοινωνιών και γενικότερα Θετικών Επιστημών και Πολυτεχνικών Σχολών
Το μάθημα στοχεύει στην ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα. Επίσης περιλαμβάνει μια εισαγωγή στην κλασική στατιστική συμπερασματολογία. Η δομή του έχει ως εξής:
- Δειγματικός χώρος και ενδεχόμενα. Αξιωματική θεμελίωση της Θεωρίας Πιθανοτήτων.
- Δεσμευμένη πιθανότητα.
- Θεώρημα ολικής πιθανότητας και κανόνας του Bayes.
- Ανεξαρτησία.
- Βασικές αρχές απαρίθμησης. Πεπερασμένοι δειγματικοί χώροι και κλασική πιθανότητα.
- Διακριτές τυχαίες μεταβλητές: Συνάρτηση (μάζας) πιθανότητας, μέση τιμή και διασπορά.
- Πολυδιάστατες διακριτές τυχαίες μεταβλητές: Από κοινού συνάρτηση (μάζας) πιθανότητας, δέσμευση, ανεξαρτησία.
- Συνεχείς τυχαίες μεταβλητές: Συνάρτηση πυκνότητας πιθανότητας, μέση τιμή και διασπορά.
- Πολυδιάστατες συνεχείς τυχαίες μεταβλητές: Από κοινού συνάρτηση πυκνότητας πιθανότητας, δέσμευση, ανεξαρτησία.
- Κατανομές συναρτήσεων τυχαίων μεταβλητών.
- Συνδιακύμανση (συνδιασπορά) και συσχέτιση.
- Δεσμευμένη μέση τιμή και διασπορά.
- Νόμος των Μεγάλων Αριθμών και Κεντρικό Οριακό Θεώρημα.
- Εισαγωγή στην κλασική στατιστική συμπερασματολογία.
- Εισαγωγή στην εκτιμητική και στα διαστήματα εμπιστοσύνης.
- Γραμμική παλινδρόμηση
- Εισαγωγή στους Ελέγχους υποθέσεων.
Σκοπός του μαθήματος είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση φαινομένων στα οποία υπεισέρχεται τυχαιότητα. Επίσης η κατανόηση βασικών τεχνικών για τη στατιστική ανάλυση δεδομένων.
Στο τέλος του μαθήματος ο εκπαιδευόμενος-φοιτητής θα πρέπει να είναι σε θέση:
- να μοντελοποιεί διαδικασίες και καταστάσεις που εμφανίζονται στην καθημερινή πραγματικότητα ή σε άλλες επιστημονικές περιοχές στο πλαίσιο της Θεωρίας Πιθανοτήτων
- να κατανοεί τις βασικές έννοιες της Θεωρίας Πιθανοτήτων, όπως την έννοια του δειγματικού σημείου, του δειγματικού χώρου, του ενδεχομένου, της πιθανότητας, της δεσμευμένης πιθανότητας, της τυχαίας μεταβλητής κλπ.
- να μπορεί να κάνει βασικούς υπολογισμούς πιθανοτήτων, μέσων τιμών, διασπορών κλπ. σε προβλήματα που εμπεριέχουν τυχαιότητα.
- να χρησιμοποιεί επιχειρήματα δέσμευσης για τους υπολογισμούς πιθανοτήτων, μέσων τιμών, διασπορών κλπ. σε προβλήματα που εμπεριέχουν τυχαιότητα
- να αντιλαμβάνεται διαισθητικά τα βασικά οριακά θεωρήματα της Θεωρίας Πιθανοτήτων (νόμοι των μεγάλων αριθμών, κεντρικό οριακό θεώρημα) και να μπορεί να τα χρησιμοποιεί σε προσεγγιστικούς υπολογισμούς πιθανοτήτων.
- να μπορεί να πραγματοποιεί απλές στατιστικές αναλύσεις δεδομένων, χρησιμοποιώντας βασικές τεχνικές από την εκτιμητική, τα διαστήματα εμπιστοσύνης και τους ελέγχους υποθέσεων.
Ελληνικά:
- Μπερτσεκά, Δ. και Τσιτσικλή, Γ. (2013) Εισαγωγή στις Πιθανότητες με Στοιχεία Στατιστικής. Εκδόσεις Τζιόλα, Θεσσαλονίκη.
- Δαμιανού, Χ.Χ., Παπαδάτου, Ν.Δ. και Χαραλαμπίδη, Χ.Α.(2010) Εισαγωγή στις Πιθανότητες και τη Στατιστική. Εκδόσεις Συμμετρία, Αθήνα
Αγγλικά:
- Bertsekas, D.P. and Tsitsiklis J. (2008) J. Introduction to Probability -2nd Edition, Athena Scientific.
- Walpole, R.E., Myers, R.H., Myers, S.L. and Ye, K. (2007) Probability and Statistics for Engineers and Scientists, Pearson
Διδασκαλία καθ΄ έδρας και συμπληρωματική-ενισχυτική εκπαίδευση μέσω ασύγχρονης πλατφόρμας – Ασκήσεις.
Είναι απαραίτητη η προγενέστερη επαφή του φοιτητή με τις βασικές έννοιες και τεχνικές Απειροστικού Λογισμού μιας και πολλών μεταβλητών. Ειδικότερα υπολογιστικά θέματα όπως υπολογισμοί ολοκληρωμάτων και αθροισμάτων θα πρέπει να είναι οικεία στους φοιτητές. Η επαφή με κάποιο μάθημα Διακριτών Μαθηματικών, αν και όχι απαραίτητη, είναι επιθυμητή.
Συγγράμματα:
- Μπερτσεκάς, Δ. και Τσιτσικλής, Γ. (2013) Εισαγωγή στις Πιθανότητες με Στοιχεία Στατιστικής. Εκδόσεις Τζιόλα, Θεσσαλονίκη.
- Δαμιανού, Χ.Χ., Παπαδάτου, Ν.Δ. και Χαραλαμπίδη, Χ.Α.(2010) Εισαγωγή στις Πιθανότητες και τη Στατιστική. Εκδόσεις Συμμετρία, Αθήνα.
- Walpole, R.E., Myers, R.H., Myers, S.L. and Ye, K. (2007) Probability and Statistics for Engineers and Scientists, Pearson. (In English).
Πηγές στο Διαδίκτυο:
Άλλα σχετικά ανοικτά μαθήματα άλλων ιδρυμάτων εσωτερικού ή εξωτερικού:
- Probabilistic Systems Analysis and Applied Probability MITOpenCourseware: http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-041-probabilistic-systems-analysis-and-applied-probability-fall-2010/index.htm
 Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Σπουδές: Πτυχίο Μαθηματικών Πανεπιστημίου Αθηνών (1993), Μεταπτυχιακό στα Θεωρητικά Μαθηματικά UCLA (1994), Μεταπτυχιακό στη Στατιστική και Επιχειρησιακή Έρευνα Πανεπιστημίου Αθηνών (1997) και Διδακτορικό στα Μαθηματικά Πανεπιστημίου Αθηνών (1998). Ερευνητικά ενδιαφέροντα: Πιθανότητες, Επιχειρησιακή Έρευνα, Μαθηματική Βιολογία. Ειδικότερα, προβλήματα υπολογισμών, στοχαστικών συγκρίσεων και βελτιστοποίησης σε στοχαστικές διαδικασίες με εφαρμογές στη θεωρία συστημάτων εξυπηρέτησης (θεωρία ουρών) και στα στοχαστικά πρότυπα εξέλιξης πληθυσμών.
http://users.uoa.gr/~aeconom/CVpdf.pdf
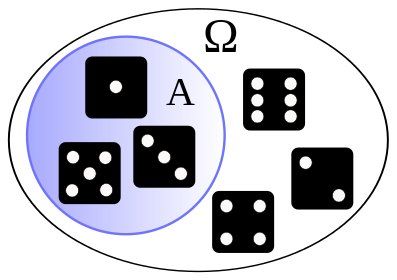 |
Έννοιες πειράματος τύχης, δειγματικού σημείου, δειγματικού χώρου, ενδεχομένου και πιθανότητας. Διαισθητικές έννοιες της πιθανότητας. Αξιωματική θεμελίωση του Kolmogorov. Βασικές ιδιότητες της συνολοσυνάρτησης της πιθανότητας. Αρχές απαρίθμησης και κλασική πιθανότητα. |
| Δεσμευμένη πιθανότητα. Πολλαπλασιαστικός νόμος, Θεώρημα ολικής πιθανότητας και κανόνας του Bayes. Στοχαστική ανεξαρτησία ενδεχομένων. | 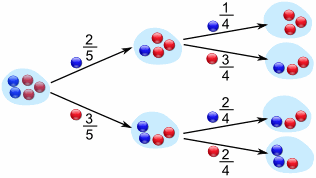 |
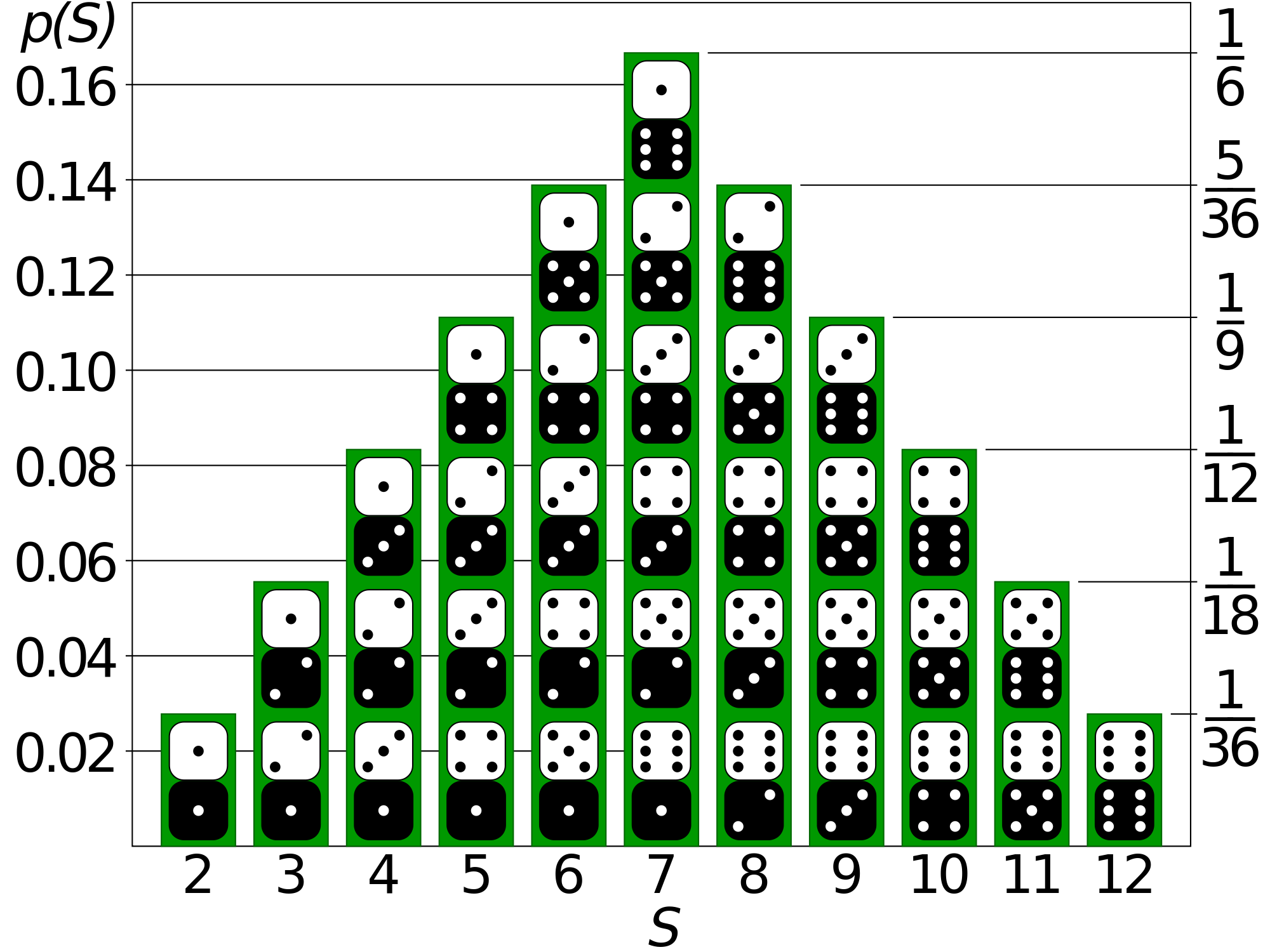 |
Έννοια της τυχαίας μεταβλητής και της διακριτής τυχαίας μεταβλητής. Συνάρτηση πιθανότητας, μέση τιμή, διασπορά. Συνάρτηση τυχαίας μεταβλητής. Βασικές διακριτές κατανομές. |
| Έννοια της συνεχούς τυχαίας μεταβλητής. Συνάρτηση πυκνότητας πιθανότητας, μέση τιμή, διασπορά. Συνάρτηση τυχαίας μεταβλητής. Βασικές συνεχείς κατανομές. | 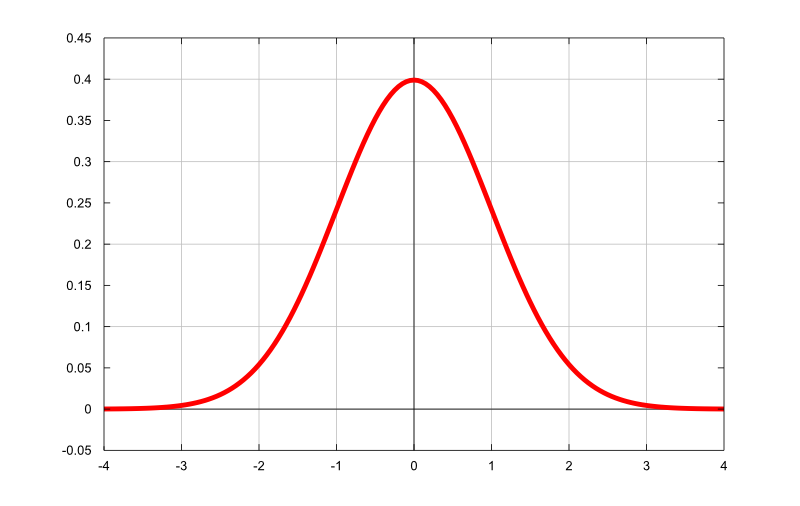 |
| Πολυδιάστατη τυχαία μεταβλητή, από κοινού συνάρτηση κατανομής, περιθώρια συνάρτηση κατανομής, δεσμευμένες συναρτήσεις κατανομής. Συνδιακύμανση, συντελεστής (γραμμικής) συσχέτισης. Δεμευμένη μέση τιμή, θεώρημα της διπλής μέσης τιμής. | 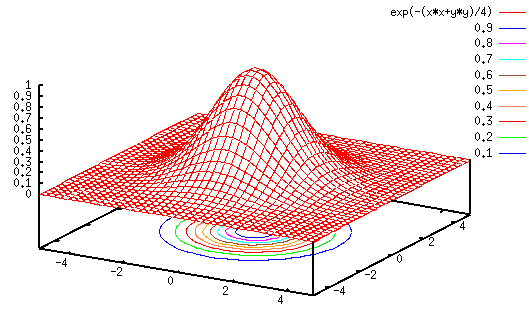 |
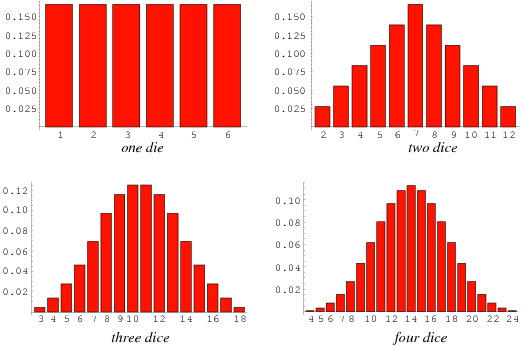 |
Ανισότητες στη Θεωρία Πιθανοτήτων. Ο Νόμος των Μεγάλων Αριθμών. Το Κεντρικό Οριακό Θεώρημα. |
 |
Το πλαίσιο της κλασικής στατιστικής συμπερασματολογίας. Εκτιμήτριες, διαστήματα εμπιστοσύνης και έλεγχοι υποθέσεων. |
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -
