Ειδική Θεωρία της Σχετικότητας
Θεοδόσιος Χριστοδουλάκης, Θεοχάρης Αποστολάτος
Το μάθημα πραγματεύεται το χωρόχρονο Minkowski και τις συμμετρίες αυτού που είναι οι μετασχηματισμοί Lorentz.
Αρχικώς παρατίθενται οι βασικές προαπαιτούμενες μαθηματικές γνώσεις από τη Θεωρία Πινάκων και τον Τανυστικό Λογισμό (ορθογώνιοι πίνακες, παραμετρική μορφή καμπύλης, συναρτησοειδή) και παραδείγματα από τη Φυσική.
Εν συνεχεία, εισάγεται η έννοια του αδρανειακού συστήματος κατά Γαλιλαίο και παρουσιάζεται το έναυσμα που οδήγησε στην ανάγκη εισαγωγής της έννοιας του χωροχρόνου Minkowski, δηλαδή, το πειραματικό δεδομένο της σταθερότητος της ταχύτητας του φωτός ανεξαρτήτως αδρανειακού παρατηρητή. Το γεγονός αυτό οδηγεί στην ανάγκη νέας μηχανικής η οποία εδράζεται στους μετασχηματισμούς Lorentz ως βασικής συμμετρίας και είναι η ειδική θεωρία της σχετικότητας. Τα γεωμετρικά μεγέθη της θεωρίας αυτής αντιστοιχούν σε φυσικές οντότητες και οι πράξεις μεταξύ αυτών συνιστούν τον τανυστικό λογισμό.
Η θεωρία του Ηλεκτρομαγνητισμού του Maxwell αναδιατυπώνεται κατά τρόπο ο οποίος κάνει προφανή την αναλλοιότητά της κάτω από τους μετασχηματισμούς Lorentz. Η εισαγωγή της νέας αυτής ομάδας συμμετρίας παράγει επίσης μια νέα σχετικιστική δυναμική.
Τέλος, αναλύονται ορισμένες βασικές εφαρμογές (διαστολή του χρόνου, συστολή του μήκους, φαινόμενο Doppler κτλ).
Το ηλεκτρονικό βιβλίο του μαθήματος στο αποθετήριο της δράσης "Ελληνικά Ακαδημαϊκά Ηλεκτρονικά Συγγράματα και Βοηθήματα" βρίσκεται στον σύνδεσμο
Το μάθημα πραγματεύεται το χωρόχρονο Minkowski και τις συμμετρίες αυτού που είναι οι μετασχηματισμοί Lorentz.
Αρχικώς παρατίθενται οι βασικές προαπαιτούμενες μαθηματικές γνώσεις από τη Θεωρία Πινάκων και τον Τανυστικό Λογισμό (ορθογώνιοι πίνακες, παραμετρική μορφή καμπύλης, συναρτησοειδή) και παραδείγματα από τη Φυσική.
Εν συνεχεία, εισάγεται η έννοια του αδρανειακού συστήματος κατά Γαλιλαίο και παρουσιάζεται το έναυσμα που οδήγησε στην ανάγκη εισαγωγής της έννοιας του χωροχρόνου Minkowski, δηλαδή, το πειραματικό δεδομένο της σταθερότητος της ταχύτητας του φωτός ανεξαρτήτως αδρανειακού παρατηρητή. Το γεγονός αυτό οδηγεί στην ανάγκη νέας μηχανικής η οποία εδράζεται στους μετασχηματισμούς Lorentz ως βασικής συμμετρίας και είναι η ειδική θεωρία της σχετικότητας. Τα γεωμετρικά μεγέθη της θεωρίας αυτής αντιστοιχούν σε φυσικές οντότητες και οι πράξεις μεταξύ αυτών συνιστούν τον τανυστικό λογισμό.
Η θεωρία του Ηλεκτρομαγνητισμού του Maxwell αναδιατυπώνεται κατά τρόπο ο οποίος κάνει προφαν
Το μάθημα πραγματεύεται το χωρόχρονο Minkowski και τις συμμετρίες αυτού που είναι οι μετασχηματισμοί Lorentz.
Αρχικώς παρατίθενται οι βασικές προαπαιτούμενες μαθηματικές γνώσεις από τη Θεωρία Πινάκων και τον Τανυστικό Λογισμό (ορθογώνιοι πίνακες, παραμετρική μορφή καμπύλης, συναρτησοειδή) και παραδείγματα από τη Φυσική.
Εν συνεχεία, εισάγεται η έννοια του αδρανειακού συστήματος κατά Γαλιλαίο και παρουσιάζεται το έναυσμα που οδήγησε στην ανάγκη εισαγωγής της έννοιας του χωροχρόνου Minkowski, δηλαδή, το πειραματικό δεδομένο της σταθερότητος της ταχύτητας του φωτός ανεξαρτήτως αδρανειακού παρατηρητή. Το γεγονός αυτό οδηγεί στην ανάγκη νέας μηχανικής η οποία εδράζεται στους μετασχηματισμούς Lorentz ως βασικής συμμετρίας και είναι η ειδική θεωρία της σχετικότητας. Τα γεωμετρικά μεγέθη της θεωρίας αυτής αντιστοιχούν σε φυσικές οντότητες και οι πράξεις μεταξύ αυτών συνιστούν τον τανυστικό λογισμό.
Η θεωρία του Ηλεκτρομαγνητισμού του Maxwell αναδιατυπώνεται κατά τρόπο ο οποίος κάνει προφαν
Περίγραμμα
Μαθησιακοί στόχοι
- Η εξοικείωση των φοιτητών με τις έννοιες των αδρανειακών συστημάτων, των χωροχρονικών μετασχηματισμών, των συμμετριών φυσικών συστημάτων
- Η ανάλυση και μελέτη των μετασχηματισμών Lorentz, του ηλεκτρομαγνητικού πεδίου και της σχετικιστικής δυναμικής
Περιεχόμενο μαθήματος
ΕΝΟΤΗΤΑ 1η - ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΓΝΩΣΕΙΣ
1.1. Υπενθυμίσεις από την θεωρία πινάκων
1.2. Μεταθέσεις – Στροφές συστήματος αναφοράς – Ορθογώνιοι πίνακες
1.2.1. Μεταθέσεις
1.2.2. Στροφές
1.2.3. Ορθογώνιοι πίνακες
1.3. Παραμετρική μορφή καμπύλης –Επαναπαραμετροποίηση καμπύλης
1.3.1. Παραμετρική μορφή καμπύλης
1.3.2. Επαναπαραμετροποίηση Καμπύλης
1.4. Συναρτησοειδή –Συναρτησοειδές του Dirac
1.4.1. Τα μαθηματικά
1.4.2. To φυσικό πρόβλημα
1.4.3. Η μαθηματική επίλυση του προβλήματος
1.4.4. Εφαρμογές στη φυσική
ΕΝΟΤΗΤΑ 2η - ΑΔΡΑΝΕΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΓΑΛΙΛΑΙΟΥ
2.1. Αδρανειακά Συστήματα αναφοράς
2.2. Μετασχηματισμός Γαλιλαίου
2.2.1. Χρονικές μεταθέσεις
2.2.2. Χωρικές μεταθέσεις
2.2.3. Χωρικές στροφές
2.2.4. Προωθήσεις Γαλιλαίου
2.2.5. Γενικός μετασχηματισμός Γαλιλαίου
2.3. Νόμος μετασχηματισμού των φυσικών μεγεθών
2.4. Η εμβέλεια και τα όρια του Μετασχηματισμού του Γαλιλαίου
2.4.1. Η εμβέλεια
2.4.2. Τα όρια
ΕΝΟΤΗΤΑ 3η - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ LORENTZ
3.1. Εισαγωγή
3.2. Προώθηση Lorentz
3.2.1. Προώθηση κατά μήκος ενός άξονα
3.2.2. Χωροχρονικές συντεταγμένες – Γενική προώθηση Lorentz
3.3. Χωροχρονική απόσταση και ο χώρος Minkowski
3.4. Ομάδα Lorentz
3.5. Σύνοψη και τυπολόγιο
ΕΝΟΤΗΤΑ 4η - ΤΑ ΜΕΓΕΘΗ ΤΗΣ ΕΙΔΙΚΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
4.1. Εισαγωγή
4.2. Χωροχρονική απόσταση και ιδιόχρονος
4.3. Τετραταχύτητα
4.4. Τετραεπιτάχυνση
4.5. Τετραορμή
ΕΝΟΤΗΤΑ 5η - ΤΑΝΥΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
5.1. Εισαγωγή
5.2. Τανυστές - Τανυστικά πεδία
5.3. Σταθεροί τανυστές
5.4. Πράξεις μεταξύ τανυστών
ΕΝΟΤΗΤΑ 6 η - ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ
6.1. Εισαγωγή
6.2. Οι πηγές
6.3. Οι εξισώσεις του Maxwell
6.4. Ο νόμος μετασχηματισμού των πεδίων
6.5. Τα αναλλοίωτα του ηλεκτρομαγνητικού πεδίου
ΕΝΟΤΗΤΑ 7 η - ΣΧΕΤΙΚΙΣΤΙΚΗ ΔΥΝΑΜΙΚΗ
7.1. Γενικά
7.2. Εφαρμογή (Τετραδύναμη Lorentz)
ΕΝΟΤΗΤΑ 8η - ΕΦΑΡΜΟΓΕΣ
8.1. Διαστολή του χρόνου
8.2. Συστολή του μήκους
8.3. Φαινόμενο Doppler (Ειδική περίπτωση)
8.4. Φαινόμενο Doppler (Γενική περίπτωση)
8.5. Μη κεντρική ελαστική κρούση
8.6. Απορρόφηση φωτονίου από ακίνητο σωματίδιο
8.7. Εκπομπή φωτονίου από ακίνητο σωμάτιο
8.8. Εκπομπή φωτονίου από κινούμενο σωμάτιο
8.9. Ενέργεια κατωφλίου
8.10. Ελαστική σκέδαση
ΕΝΟΤΗΤΑ 9η - ΑΣΚΗΣΕΙΣ
9.1. Μετασχηματισμός Lorentz
9.2. Χώρος Minkowski
9.3. Τετραταχύτητα - Τετραορμή
9.4. Τανυστικός λογισμός
9.5. Διατήρηση ορμής - ενέργειας
9.6. Ηλεκτρομαγνητισμός
Διδάσκοντες
Θεοδόσιος Χριστοδουλάκης (βιογραφικό στην επιλογή Σύνδεσμοι)
Θεοχάρης Αποστολάτος (βιογραφικό στην επιλογή Σύνδεσμοι)
Ομάδα στόχος
Προπτυχιακοί φοιτητές και πτυχιούχοι τμημάτων Σχολών Θετικών Επιστημών (Φυσικής, Μαθηματικών, κ.α)
Προτεινόμενα συγγράμματα
- Ειδική Θεωρία της Σχετικότητας - Χριστοδουλάκης Θεοδόσιος, Κορφιάτης Ευάγγελος, Ελληνικά Ακαδημαϊκά Συγγράμματα και Βοηθήματα.
- Εισαγωγή στην Ειδική Σχετικότητα - Wolfgang Rindler - Εκδόσεις Leader Books (ελληνική μετάφραση)
- Γενική Σχετικότητα - Bernard Schutz- Εκδόσεις Π. Τραυλός (ελληνική μετάφραση) - Τα τέσσερα πρώτα κεφάλαια
- Θεωρία της Ειδικής Σχετικότητας - Μιχάλης Τσαμπαρλής- Μέρος Ι και Μέρος ΙΙ
- Relativity: The special theory-J. Synge- North Holland
- Introduction to the theory of relativity - Bergmann- Dover publications
Μέθοδοι διδασκαλίας
- Διδασκαλία από καθ’ έδρας
- Φροντιστήριο
Προαπαιτούμενα
- Κλασική Μηχανική
- Θεωρία Πινάκων
- Η εξοικείωση των φοιτητών με τις έννοιες των αδρανειακών συστημάτων, των χωροχρονικών μετασχηματισμών, των συμμετριών φυσικών συστημάτων
- Η ανάλυση και μελέτη των μετασχηματισμών Lorentz, του ηλεκτρομαγνητικού πεδίου και της σχετικιστικής δυναμικής
ΕΝΟΤΗΤΑ 1η - ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΓΝΩΣΕΙΣ
1.1. Υπενθυμίσεις από την θεωρία πινάκων
1.2. Μεταθέσεις – Στροφές συστήματος αναφοράς – Ορθογώνιοι πίνακες
1.2.1. Μεταθέσεις
1.2.2. Στροφές
1.2.3. Ορθογώνιοι πίνακες
1.3. Παραμετρική μορφή καμπύλης –Επαναπαραμετροποίηση καμπύλης
1.3.1. Παραμετρική μορφή καμπύλης
1.3.2. Επαναπαραμετροποίηση Καμπύλης
1.4. Συναρτησοειδή –Συναρτησοειδές του Dirac
1.4.1. Τα μαθηματικά
1.4.2. To φυσικό πρόβλημα
1.4.3. Η μαθηματική επίλυση του προβλήματος
1.4.4. Εφαρμογές στη φυσική
ΕΝΟΤΗΤΑ 2η - ΑΔΡΑΝΕΙΑΚΑ ΣΥΣΤΗΜΑΤΑ ΑΝΑΦΟΡΑΣ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΓΑΛΙΛΑΙΟΥ
2.1. Αδρανειακά Συστήματα αναφοράς
2.2. Μετασχηματισμός Γαλιλαίου
2.2.1. Χρονικές μεταθέσεις
2.2.2. Χωρικές μεταθέσεις
2.2.3. Χωρικές στροφές
2.2.4. Προωθήσεις Γαλιλαίου
2.2.5. Γενικός μετασχηματισμός Γαλιλαίου
2.3. Νόμος μετασχηματισμού των φυσικών μεγεθών
2.4. Η εμβέλεια και τα όρια του Μετασχηματισμού του Γαλιλαίου
2.4.1. Η εμβέλεια
2.4.2. Τα όρια
ΕΝΟΤΗΤΑ 3η - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ LORENTZ
3.1. Εισαγωγή
3.2. Προώθηση Lorentz
3.2.1. Προώθηση κατά μήκος ενός άξονα
3.2.2. Χωροχρονικές συντεταγμένες – Γενική προώθηση Lorentz
3.3. Χωροχρονική απόσταση και ο χώρος Minkowski
3.4. Ομάδα Lorentz
3.5. Σύνοψη και τυπολόγιο
ΕΝΟΤΗΤΑ 4η - ΤΑ ΜΕΓΕΘΗ ΤΗΣ ΕΙΔΙΚΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ
4.1. Εισαγωγή
4.2. Χωροχρονική απόσταση και ιδιόχρονος
4.3. Τετραταχύτητα
4.4. Τετραεπιτάχυνση
4.5. Τετραορμή
ΕΝΟΤΗΤΑ 5η - ΤΑΝΥΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ
5.1. Εισαγωγή
5.2. Τανυστές - Τανυστικά πεδία
5.3. Σταθεροί τανυστές
5.4. Πράξεις μεταξύ τανυστών
ΕΝΟΤΗΤΑ 6 η - ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ
6.1. Εισαγωγή
6.2. Οι πηγές
6.3. Οι εξισώσεις του Maxwell
6.4. Ο νόμος μετασχηματισμού των πεδίων
6.5. Τα αναλλοίωτα του ηλεκτρομαγνητικού πεδίου
ΕΝΟΤΗΤΑ 7 η - ΣΧΕΤΙΚΙΣΤΙΚΗ ΔΥΝΑΜΙΚΗ
7.1. Γενικά
7.2. Εφαρμογή (Τετραδύναμη Lorentz)
ΕΝΟΤΗΤΑ 8η - ΕΦΑΡΜΟΓΕΣ
8.1. Διαστολή του χρόνου
8.2. Συστολή του μήκους
8.3. Φαινόμενο Doppler (Ειδική περίπτωση)
8.4. Φαινόμενο Doppler (Γενική περίπτωση)
8.5. Μη κεντρική ελαστική κρούση
8.6. Απορρόφηση φωτονίου από ακίνητο σωματίδιο
8.7. Εκπομπή φωτονίου από ακίνητο σωμάτιο
8.8. Εκπομπή φωτονίου από κινούμενο σωμάτιο
8.9. Ενέργεια κατωφλίου
8.10. Ελαστική σκέδαση
ΕΝΟΤΗΤΑ 9η - ΑΣΚΗΣΕΙΣ
9.1. Μετασχηματισμός Lorentz
9.2. Χώρος Minkowski
9.3. Τετραταχύτητα - Τετραορμή
9.4. Τανυστικός λογισμός
9.5. Διατήρηση ορμής - ενέργειας
9.6. Ηλεκτρομαγνητισμός
Θεοδόσιος Χριστοδουλάκης (βιογραφικό στην επιλογή Σύνδεσμοι)
Θεοχάρης Αποστολάτος (βιογραφικό στην επιλογή Σύνδεσμοι)
Προπτυχιακοί φοιτητές και πτυχιούχοι τμημάτων Σχολών Θετικών Επιστημών (Φυσικής, Μαθηματικών, κ.α)
- Ειδική Θεωρία της Σχετικότητας - Χριστοδουλάκης Θεοδόσιος, Κορφιάτης Ευάγγελος, Ελληνικά Ακαδημαϊκά Συγγράμματα και Βοηθήματα.
- Εισαγωγή στην Ειδική Σχετικότητα - Wolfgang Rindler - Εκδόσεις Leader Books (ελληνική μετάφραση)
- Γενική Σχετικότητα - Bernard Schutz- Εκδόσεις Π. Τραυλός (ελληνική μετάφραση) - Τα τέσσερα πρώτα κεφάλαια
- Θεωρία της Ειδικής Σχετικότητας - Μιχάλης Τσαμπαρλής- Μέρος Ι και Μέρος ΙΙ
- Relativity: The special theory-J. Synge- North Holland
- Introduction to the theory of relativity - Bergmann- Dover publications
- Διδασκαλία από καθ’ έδρας
- Φροντιστήριο
- Κλασική Μηχανική
- Θεωρία Πινάκων
Υπενθυμίσεις από τη θεωρία πινάκων. Μεταθέσεις-Στροφές συστήματος αναφοράς. Ορθογώνιοι Πίνακες. Παραμετρική μορφή καμπύλης. Επαναπαραμετροποίηση καμπύλης. Συναρτησιοειδή. Συναρτησιοειδές του Dirac.
Λέξεις κλειδιά: ανάστροφος πίνακα, πράξεις πινάκων, μετάθεση, στροφή, συνθήκη άθροισης Einstein, Ευκλείδειος μετρικός τανυστής, δέλτα του Kronecker, συναλλοίωτος δείκτης, ανταλλοίωτος δείκτης, ορθογώνιος πίνακας, παραμετρική μορφή καμπύλης, ταχύτητα καμπύλης, επιτάχυνση καμπύλης, συναρτησοειδής, συναρτησοειδές του Dirac
Αδρανειακά Συστήματα Αναφοράς. Μετασχηματισμός Γαλιλαίου (χρονικές μεταθέσεις, χωρικές μεταθέσεις, χωρικές στροφές, προωθήσεις Γαλιλαίου, Γενικός Μετασχηματισμός Γαλιλαίου). Νόμος μετασχηματισμού των φυσικών μεγεθών. Η εμβέλεια και τα όρια του Μετασχηματισμού του Γαλιλαίου.
Λέξεις Κλειδιά:αδρανειακό σύστημα αναφοράς, χρονική μετάθεση, χωρική μετάθεση, χωροχρονική μετάθεση, χωρική στροφή, προώθηση Γαλιλαίου, γενικός μετασχηματισμός Γαλιλαίου
Προώθηση Lorentz, Χωροχρονική απόσταση. Χώρος Minkowski. Ομάδα Lorentz.
Λέξεις Κλειδιά: προώθηση Lorentz, διαστολή χρόνου, συστολή μήκους, γενική προώθηση Lorentz, χωροχρονική απόσταση γεγονότων, μετρικός τανυστής, ομάδα Lorentz
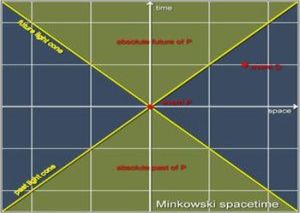Χωροχρονική απόσταση. Ιδιόχρονος. Τετραταχύτητα. Τετραεπιτάχυνση. Τετραορμή.
Λέξεις Κλειδιά: ιδιόχρονος, τετραταχύτητα, τετραεπιτάχυνση, ενέργεια ηρεμίας, σχετικιστική κινητική ενέργεια, τετραορμή
Τανυστές - Τανυστικά πεδία, Σταθεροί τανυστές, Πράξεις μεταξύ τανυστών
Λέξεις Κλειδιά: Τανυστές - Τανυστικά πεδία, Σταθεροί τανυστές, Πράξεις μεταξύ τανυστών
Πηγές ηλεκτρομαγνητικού πεδίου, εξισώσεις του Maxwell, vόμος μετασχηματισμού των πεδίων, αναλλοίωτα του ηλεκτρομαγνητικού πεδίου
Λέξεις Κλειδιά: Πηγές ηλεκτρομαγνητικού πεδίου, εξισώσεις του Maxwell, vόμος μετασχηματισμού των πεδίων, αναλλοίωτα του ηλεκτρομαγνητικού πεδίου
Διαστολή του χρόνου, συστολή του μήκους, φαινόμενο Doppler (Ειδική και γενική περίπτωση), μη κεντρική ελαστική κρούση, απορρόφηση φωτονίου από ακίνητο σωματίδιο, εκπομπή φωτονίου από ακίνητο σωμάτιο, εκπομπή φωτονίου από κινούμενο σωμάτιο, ενέργεια κατωφλίου, ελαστική σκέδαση
Λέξεις Κλειδιά: διαστολή του χρόνου, συστολή του μήκους, φαινόμενο Doppler (Ειδική και γενική περίπτωση), μη κεντρική ελαστική κρούση, απορρόφηση φωτονίου από ακίνητο σωματίδιο, εκπομπή φωτονίου από ακίνητο σωμάτιο, εκπομπή φωτονίου από κινούμενο σωμάτιο, ενέργεια κατωφλίου, ελαστική σκέδαση
Ανοικτό Ακαδ. Μάθημα
Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
