Σειρές Fourier και ολοκλήρωμα Lebesgue
Απόστολος Γιαννόπουλος
Ανάλυση Fourier και Ολοκλήρωμα Lebesgue
Το περιεχόμενο του μαθήματος είναι:
- Μέτρο Lebesgue στην ευθεία και στο επίπεδο, μετρήσιμες συναρτήσεις, ολοκλήρωμα Lebesgue, βασικά θεωρήματα σύγκλισης.
- Σχέση με το ολοκλήρωμα Riemann, συναρτήσεις φραγμένης κύμανσης, απόλυτα συνεχείς συναρτήσεις, θεώρημα παραγώγισης του Lebesgue.
- Χώροι Lp, Θεώρημα Fubini, Συνέλιξη. Γεωμετρία του χώρου L2.
- Σειρές Fourier, κριτήρια σημειακής σύγκλισης, συνεχείς συναρτήσεις με αποκλίνουσα σειρά Fourier.
- Αθροισιμότητα, πυρήνας του Fejer, πυρήνας του Poisson.
- L2-σύγκλιση.
- Μετασχηματισμός Fourier, τύπος αντιστροφής, θεώρημα Plancherel, τύπος άθροισης του Poisson.
- Διάφορες εφαρμογές.
Ανάλυση Fourier και Ολοκλήρωμα Lebesgue
Το περιεχόμενο του μαθήματος είναι:
- Μέτρο Lebesgue στην ευθεία και στο επίπεδο, μετρήσιμες συναρτήσεις, ολοκλήρωμα Lebesgue, βασικά θεωρήματα σύγκλισης.
- Σχέση με το ολοκλήρωμα Riemann, συναρτήσεις φραγμένης κύμανσης, απόλυτα συνεχείς συναρτήσεις, θεώρημα παραγώγισης του Lebesgue.
- Χώροι Lp, Θεώρημα Fubini, Συνέλιξη. Γεωμετρία του χώρου L2.
- Σειρές Fourier, κριτήρια σημειακής σύγκλισης, συνεχείς συναρτήσεις με αποκλίνουσα σειρά Fourier.
- Αθροισιμότητα, πυρήνας του Fejer, πυρήνας του Poisson.
- L2-σύγκλιση.
- Μετασχηματισμός Fourier, τύπος αντιστροφής, θεώρημα Plancherel, τύπος άθροισης του Poisson.
- Διάφορες εφαρμογές.
Ανάλυση Fourier και Ολοκλήρωμα Lebesgue
Το περιεχόμενο του μαθήματος είναι:
- Μέτρο Lebesgue στην ευθεία και στο επίπεδο, μετρήσιμες συναρτήσεις, ολοκλήρωμα Lebesgue, βασικά θεωρήματα σύγκλισης.
- Σχέση με το ολοκλήρωμα Riemann, συναρτήσεις φραγμένης κύμανσης, απόλυτα συνεχείς συναρτήσεις, θεώρημα παραγώγισης του Lebesgue.
- Χώροι Lp, Θεώρημα Fubini, Συνέλιξη. Γεωμετρία του χώρου L2.
- Σειρές Fourier, κριτήρια σημειακής σύγκλισης, συνεχείς συναρτήσεις με αποκλίνουσα σειρά Fourier.
- Αθροισιμότητα, πυρήνας του Fejer, πυρήνας του Poisson.
- L2-σύγκλιση.
- Μετασχηματισμός Fourier, τύπος αντιστροφής, θεώρημα Plancherel, τύπος άθροισης του Poisson.
- Διάφορες εφαρμογές.
Περίγραμμα

Περιεχόμενο μαθήματος
- Μέτρο Lebesgue
- Εξωτερικό μέτρο Lebesgue
- Lebesgue μετρήσιμα σύνολα
- Μέτρο Lebesgue
- Το σύνολο του Cantor και το σύνολο του Vitali
- Ολοκλήρωμα Lebesgue
- Μετρήσιμες συναρτήσεις
- Ολοκλήρωμα Lebesgue
- Ολοκλήρωμα Riemann και Ολοκλήρωμα Lebesgue
- Σύγκριση του ολοκληρώματος Lebesgue με το ολοκλήρωμα Riemann
- Το θεώρημα παραγώγισης του Lebesgue
- Συναρτήσεις φραγμένης κύμανσης
- Παραγωγισιμότητα μονότονων συναρτήσεων
- Απόλυτα συνεχείς συναρτήσεις
- Χώροι Lp
- Χώροι Lp
- Θεώρημα Riesz-Fischer
- Θεώρημα Fubini
- Συνέλιξη
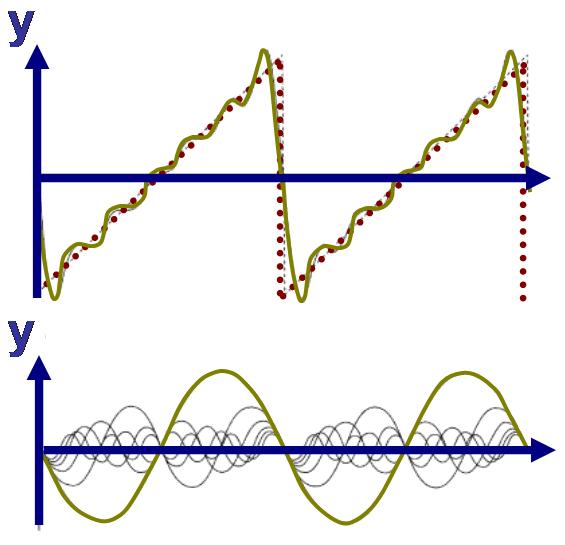
- Σειρές Fourier
- Σειρές Fourier ολοκληρώσιμων συναρτήσεων
- Τριγωνομετρικά πολυώνυμα
- Βασικές ιδιότητες των σειρών Fourier
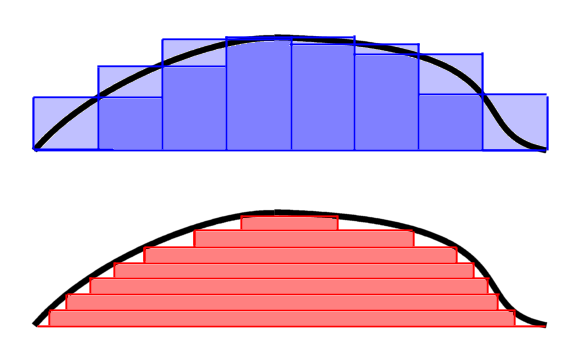
- Ο πυρήνας του Dirichlet
- Σειρές Fourier συνεχών συναρτήσεων
- Θεώρημα Dini και θεώρημα Marcinkiewicz
- Προσεγγίσεις της μονάδας και Αθροισιμότητα
- Οικογένειες καλών πυρήνων και προσεγγίσεων της μονάδας
- Cesaro αθροισιμότητα
- Ο πυρήνας του Fejer
- Χαρακτηρισμός των τριγωνομετρικών σειρών που είναι σειρές Fourier
- Abel αθροισιμότητα και ο πυρήνας του Poisson
- L2-σύγκλιση σειρών Fourier
- Χώροι Hilbert
- Σύγκλιση στον L2 (T)
Διδάσκοντες
Γιαννόπουλος Απόστολος
Θέση : Καθηγητής
Τομέας : Μαθηματικής Ανάλυσης
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Βιβλιογραφία
- W. Rudin: Αρχές Μαθηματικής Αναλύσεως (Μεταφ. Δ.Κ. Σταλίδη). Εκδ. Leader Books, 2000 (τίτλος πρωτοτύπου: Principles of Mathematical Analysis, McGraw-Hill, 1976).
- Σ. Νεγρεπόντης, Σ. Γιωτόπουλος, Σ. Γιαννακούλιας: Απειροστικός Λογισμός ΙΙβ, Κεφ. 30. Εκδ. Συμμετρία, 1993.
- K. R. Davidson, A. P. Donsig: Real Analysis with Real Applications, Prentice Hall, 2002.
- T. W. Körner: Fourier Analysis, Cambridge University Press, 1988.
- N. L. Carothers: Real Analysis, Cambridge University Press, 2000.
- E. M. Stein & R. Shakarchi: Fourier Analysis, an introduction, Princeton University Press, 2003.
Συμπληρωματική Βιβλιογραφία
- Y. Katznelson: An introduction to Harmonic Analysis, Dover, 1976.
- G. Bachman, L. Narici, E. Beckenstein: Fourier and Wavelet Analysis, Springer, 2002.
- Γ. Κουμουλλής, Σ. Νεγρεπόντης: Θεωρία Μέτρου, Εκδ. Συμμετρία, 1988.
Προαπαιτούμενα
Απειροστικός Λογισμός μιάς πραγματικής μεταβλητής.
Ακολουθίες και σειρές συναρτήσεων: σημειακή και ομοιόμορφη σύγκλιση.
Δεν απαιτείται γνώση μετρικών χώρων ή χώρων με νόρμα.
Σημειώματα Δικαιωμάτων Πνευματικής Ιδιοκτησίας
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Απόστολος Γιαννόπουλος. Σειρές Fourier και ολοκλήρωμα Lebesgue. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH5/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».
[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Μέτρο Lebesgue
- Εξωτερικό μέτρο Lebesgue
- Lebesgue μετρήσιμα σύνολα
- Μέτρο Lebesgue
- Το σύνολο του Cantor και το σύνολο του Vitali
- Ολοκλήρωμα Lebesgue
- Μετρήσιμες συναρτήσεις
- Ολοκλήρωμα Lebesgue
- Ολοκλήρωμα Riemann και Ολοκλήρωμα Lebesgue
- Σύγκριση του ολοκληρώματος Lebesgue με το ολοκλήρωμα Riemann
- Το θεώρημα παραγώγισης του Lebesgue
- Συναρτήσεις φραγμένης κύμανσης
- Παραγωγισιμότητα μονότονων συναρτήσεων
- Απόλυτα συνεχείς συναρτήσεις
- Χώροι Lp
- Χώροι Lp
- Θεώρημα Riesz-Fischer
- Θεώρημα Fubini
- Συνέλιξη
- Σειρές Fourier
- Σειρές Fourier ολοκληρώσιμων συναρτήσεων
- Τριγωνομετρικά πολυώνυμα
- Βασικές ιδιότητες των σειρών Fourier
- Ο πυρήνας του Dirichlet
- Σειρές Fourier συνεχών συναρτήσεων
- Θεώρημα Dini και θεώρημα Marcinkiewicz
- Προσεγγίσεις της μονάδας και Αθροισιμότητα
- Οικογένειες καλών πυρήνων και προσεγγίσεων της μονάδας
- Cesaro αθροισιμότητα
- Ο πυρήνας του Fejer
- Χαρακτηρισμός των τριγωνομετρικών σειρών που είναι σειρές Fourier
- Abel αθροισιμότητα και ο πυρήνας του Poisson
- L2-σύγκλιση σειρών Fourier
- Χώροι Hilbert
- Σύγκλιση στον L2 (T)
Γιαννόπουλος Απόστολος
Θέση : Καθηγητής
Τομέας : Μαθηματικής Ανάλυσης
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
- W. Rudin: Αρχές Μαθηματικής Αναλύσεως (Μεταφ. Δ.Κ. Σταλίδη). Εκδ. Leader Books, 2000 (τίτλος πρωτοτύπου: Principles of Mathematical Analysis, McGraw-Hill, 1976).
- Σ. Νεγρεπόντης, Σ. Γιωτόπουλος, Σ. Γιαννακούλιας: Απειροστικός Λογισμός ΙΙβ, Κεφ. 30. Εκδ. Συμμετρία, 1993.
- K. R. Davidson, A. P. Donsig: Real Analysis with Real Applications, Prentice Hall, 2002.
- T. W. Körner: Fourier Analysis, Cambridge University Press, 1988.
- N. L. Carothers: Real Analysis, Cambridge University Press, 2000.
- E. M. Stein & R. Shakarchi: Fourier Analysis, an introduction, Princeton University Press, 2003.
- Y. Katznelson: An introduction to Harmonic Analysis, Dover, 1976.
- G. Bachman, L. Narici, E. Beckenstein: Fourier and Wavelet Analysis, Springer, 2002.
- Γ. Κουμουλλής, Σ. Νεγρεπόντης: Θεωρία Μέτρου, Εκδ. Συμμετρία, 1988.
Απειροστικός Λογισμός μιάς πραγματικής μεταβλητής.
Ακολουθίες και σειρές συναρτήσεων: σημειακή και ομοιόμορφη σύγκλιση.
Δεν απαιτείται γνώση μετρικών χώρων ή χώρων με νόρμα.
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Απόστολος Γιαννόπουλος. Σειρές Fourier και ολοκλήρωμα Lebesgue. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH5/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».

[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Σύγκριση του ολοκληρώματος Lebesgue με το ολοκλήρωμα Riemann
- Το θεώρημα παραγώγισης του Lebesgue
- Συναρτήσεις φραγμένης κύμανσης
- Παραγωγισιμότητα μονότονων συναρτήσεων
- Απόλυτα συνεχείς συναρτήσεις
Λέξεις Κλειδιά: ολοκλήρωμα Riemann, ολοκλήρωμα Lebesgue, θεώρημα παραγώγισης του Lebesgue, μεγιστική συνάρτηση των Hardy και Littlewood, συναρτήσεις φραγμένης κύμανσης, κύμανση, φραγμένη κύμανση, συνάρτηση ολικής κύμανσης, παραγωγισιμότητα μονότονων συναρτήσεων
- Εξωτερικό μέτρο Lebesgue: Ορισμός, ιδιότητες
- Lebesgue μετρήσιμα σύνολα
- Μέτρο Lebesgue
- Το σύνολο του Cantor και το σύνολο του Vitali
Λέξεις Κλειδιά: εξωτερικό μέτρο Lebesgue, μετρήσιμα σύνολα, μέτρο Lebesgue, σύνολο του Cantor, σύνολο του Vitali

- Μετρήσιμες συναρτήσεις
- Ολοκλήρωμα Lebesgue
Λέξεις Κλειδιά: μετρήσιμες συναρτήσεις, Borel μετρήσιμη, Lebesgue μετρήσιμη, ακολουθίες μετρήσιμων συναρτήσεων, συνάρτηση Cantor-Lebesgue, αρχές του Littlewood, ολοκλήρωμα Lebesgue, απλές μετρήσιμες συναρτήσεις, θεώρημα κυριαρχημένης σύγκλισης
- Σειρές Fourier ολοκληρώσιμων συναρτήσεων
- Τριγωνομετρικά πολυώνυμα
- Βασικές ιδιότητες των σειρών Fourier
- Ο πυρήνας του Dirichlet
- Σειρές Fourier συνεχών συναρτήσεων
- Θεώρημα Dini και θεώρημα Marcinkiewicz
Λέξεις Κλειδιά: σειρά Fourier, συντελεστή Fourier, τριγωνομετρικά πολυώνυμα, μοναδικότητα σειρών Fourier, πυρήνας του Dirichlet, θεώρημα Dini, θεώρημα Marcinkiewicz
![]()
- Χώροι Lp
- Θεώρημα Riesz-Fischer
- Θεώρημα Fubini
- Συνέλιξη
Λέξεις Κλειδιά: χώροι Lp, θεώρημα Riesz-Fischer, χώρος L∞, προσέγγιση συναρτήσεων στον Lp, θεώρημα Fubini, συνέλιξη
- Χώροι Hilbert
- Σύγκλιση στον L2 (T)
Λέξεις Κλειδιά: χώροι Hilbert, L2-σύγκλιση σειρών Fourier, χώροι με εσωτερικό γινόμενο, καθετότητα, ορθοκανονικές βάσεις
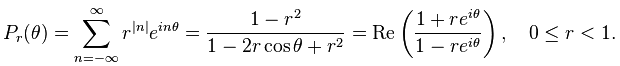
- Οικογένειες καλών πυρήνων και προσεγγίσεων της μονάδας
- Cesaro αθροισιμότητα
- Ο πυρήνας του Fejer
- Χαρακτηρισμός των τριγωνομετρικών σειρών που είναι σειρές Fourier
- Abel αθροισιμότητα και ο πυρήνας του Poisson
Λέξεις Κλειδιά: πυρήνας, οικογένεια καλών πυρήνων, προσέγγιση της μονάδας, Cesaro αθροισιμότητα, πυρήνας του Fejer, Abel αθροισιμότητα, πυρήνας του Poisson
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -