Πραγματική Ανάλυση
Απόστολος Γιαννόπουλος
Πραγματική Ανάλυση
Το περιεχόμενο του μαθήματος είναι:
- Στοιχεία από τη θεωρία συνόλων (αριθμήσιμα και υπεραριθμήσιμα σύνολα, αριθμησιμότητα του συνόλου των ρητών και υπεραριθμησιμότητα του συνόλου των πραγματικών αριθμών).
- Μετρικοί χώροι (ορισμοί, βασικές ιδιότητες και παραδείγματα, τοπολογικές έννοιες, ισοδύναμες μετρικές, φραγμένα και ολικά φραγμένα σύνολα).
- Συνέχεια συναρτήσεων σε μετρικούς χώρους: σημειακή (τοπική) συνέχεια και (ολική) συνέχεια, ιδιότητες συνεχών συναρτήσεων. Ισομετρίες, συναρτήσεις Lipschitz, ομοιόμορφη συνέχεια.
- Πληρότητα: πλήρης μετρικός χώρος (ορισμός, βασικές ιδιότητες, παραδείγματα). Θεωρήματα σταθερού σημείου (και εφαρμογές στις διαφορικές εξισώσεις). Θεωρήματα Cantor και Baire και εφαρμογές.
- Συμπάγεια: ορισμός (με ανοικτές καλύψεις), και βασικές ιδιότητες. Συνέχεια συναρτήσεων και συμπάγεια. Χαρακτηρισμοί της συμπάγειας με τη βοήθεια της ιδιότητας Bolzano-Weierstrass και της έννοιας του ολικά φραγμένου. Πεπερασμένο (καρτεσιανό) γινόμενο συμπαγών μετρικών χώρων.
- Διαχωρισιμότητα.
- Σύνολο Cantor.
- Ακολουθίες και σειρές συναρτήσεων: απλή και ομοιόμορφη σύγκλιση (ορισμοί, βασικές ιδιότητες και παραδείγματα). Κριτήριο Weierstrass (για την ομοιόμορφη σύγκλιση σειρών συναρτήσεων). Ομοιόμορφη σύγκλιση και συνέχεια, ολοκλήρωση και διαφόριση.
- Συνεχείς πραγματικές συναρτήσεις σε συμπαγείς μετρικούς χώρους: Θεώρημα προσέγγισης του Weierstrass. Η δομή του μετρικού χώρου C(X), όπου Χ συμπαγής μετρικός χώρος. Συμπάγεια και ισοσυνέχεια στον C(X). Θεώρημα Ascoli-Arzela και θεώρημα Peano.
Πραγματική Ανάλυση
Το περιεχόμενο του μαθήματος είναι:
- Στοιχεία από τη θεωρία συνόλων (αριθμήσιμα και υπεραριθμήσιμα σύνολα, αριθμησιμότητα του συνόλου των ρητών και υπεραριθμησιμότητα του συνόλου των πραγματικών αριθμών).
- Μετρικοί χώροι (ορισμοί, βασικές ιδιότητες και παραδείγματα, τοπολογικές έννοιες, ισοδύναμες μετρικές, φραγμένα και ολικά φραγμένα σύνολα).
- Συνέχεια συναρτήσεων σε μετρικούς χώρους: σημειακή (τοπική) συνέχεια και (ολική) συνέχεια, ιδιότητες συνεχών συναρτήσεων. Ισομετρίες, συναρτήσεις Lipschitz, ομοιόμορφη συνέχεια.
- Πληρότητα: πλήρης μετρικός χώρος (ορισμός, βασικές ιδιότητες, παραδείγματα). Θεωρήματα σταθερού σημείου (και εφαρμογές στις διαφορικές εξισώσεις). Θεωρήματα Cantor και Baire και εφαρμογές.
- Συμπάγεια: ορισμός (με ανοικτές καλύψεις), και βασικές ιδιότητες. Συνέχεια συναρτήσεων και συμπάγεια. Χαρακτηρισμοί της συμπάγειας με τη βοήθεια της ιδιότητας Bolzano-Weierstrass και της έννοιας του ολικά φραγμένου. Πεπερασμένο (καρτεσιανό) γινόμενο συμπαγών μετρικών χώ
Πραγματική Ανάλυση
Το περιεχόμενο του μαθήματος είναι:
- Στοιχεία από τη θεωρία συνόλων (αριθμήσιμα και υπεραριθμήσιμα σύνολα, αριθμησιμότητα του συνόλου των ρητών και υπεραριθμησιμότητα του συνόλου των πραγματικών αριθμών).
- Μετρικοί χώροι (ορισμοί, βασικές ιδιότητες και παραδείγματα, τοπολογικές έννοιες, ισοδύναμες μετρικές, φραγμένα και ολικά φραγμένα σύνολα).
- Συνέχεια συναρτήσεων σε μετρικούς χώρους: σημειακή (τοπική) συνέχεια και (ολική) συνέχεια, ιδιότητες συνεχών συναρτήσεων. Ισομετρίες, συναρτήσεις Lipschitz, ομοιόμορφη συνέχεια.
- Πληρότητα: πλήρης μετρικός χώρος (ορισμός, βασικές ιδιότητες, παραδείγματα). Θεωρήματα σταθερού σημείου (και εφαρμογές στις διαφορικές εξισώσεις). Θεωρήματα Cantor και Baire και εφαρμογές.
- Συμπάγεια: ορισμός (με ανοικτές καλύψεις), και βασικές ιδιότητες. Συνέχεια συναρτήσεων και συμπάγεια. Χαρακτηρισμοί της συμπάγειας με τη βοήθεια της ιδιότητας Bolzano-Weierstrass και της έννοιας του ολικά φραγμένου. Πεπερασμένο (καρτεσιανό) γινόμενο συμπαγών μετρικών χώ
Περίγραμμα

Περιεχόμενα
- Μετρικοί Χώροι
- Χώροι με νόρμα
- Ορισμός και παραδείγματα
- Ασκήσεις
- Σύγκλιση ακολουθιών και συνέχεια συναρτήσεων
- Σύγκλιση ακολουθιών
- Συνέχεια σε ένα σημείο και αρχή της μεταφοράς
- Ασκήσεις
- Τοπολογία μετρικών χώρων
- Ανοικτά και κλειστά σύνολα
- Εσωτερικό και κλειστή θήκη
- Σχετικώς ανοικτά και κλειστά σύνολα
- Σημεία συσσώρευσης και σύνορο
- Πυκνά σύνολα και διαχωρισιμότητα
- Ασκήσεις
- Συναρτήσεις μεταξύ μετρικών χώρων
- Συνεχείς συναρτήσεις
- Ομοιόμορφα συνεχείς συναρτήσεις
- Ισομετρίες, ομοιομορφισμοί, ισοδύναμες μετρικές
- Βασικά αποτελέσματα για συναρτήσεις σε μετρικούς χώρους
- Ασκήσεις
- Πληρότητα
- Πλήρεις μετρικοί χώροι
- Το θεώρημα του Cantor
- Το θεώρημα κατηγορίας του Baire
- Πλήρωση μετρικού χώρου*
- Το θεώρημα σταθερού σημείου του Banach
- Ασκήσεις
- Συμπάγεια
- Ορισμός της συμπάγειας
- Χαρακτηρισμός της συμπάγειας
- Βασικές ιδιότητες των συμπαγών συνόλων
- Συνεχείς συναρτήσεις σε συμπαγή σύνολα
- Το σύνολο του Cantor
- Ασκήσεις
- Ακολουθίες και σειρές συναρτήσεων
- Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση
- Ακολουθίες συναρτήσεων: ομοιόμορφη σύγκλιση
- Σειρές Συναρτήσεων
- Ασκήσεις
- Συνεχείς συναρτήσεις σε συμπαγείς μετρικούς χώρους
- Ο χώρος C(K
- Το θεώρημα προσέγγισης του Weierstrass
- Ασκήσεις
Διδάσκοντες
Γιαννόπουλος Απόστολος
Θέση : Καθηγητής
Τομέας : Μαθηματικής Ανάλυσης
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Μαθησιακοί στόχοι
Εξοικίωση του διδασκόμενου με τους μετρικούς χώρους, την συνέχεια συναρτήσεων σε μετρικούς χώρους.
Μελέτη:
- Της πληρότητας μετρικών χώρων
- Της συμπάγειας μετρικών χώρων
- Bolzano-Weierstrass και Ολικά Φραγμένα
- Διαχωρισιμότητας
- Συνόλων Cantor
- Απλής και Ομοιόμορφης σύγκλισης ακολουθιών και σειρών συναρτήσεων
- Συνεχών πραγματικών συναρτήσεων σε συμπαγείς μετρικούς χώρους
- Συμπάγειας και ισοσυνέχειας
Προαπαιτούμενα
- Απειροστικός Λογισμός I
- Απειροστικός Λογισμός II
Βιβλιογραφία
- W. Rudin: Αρχές Μαθηματικής Ανάλυσης
- Κ. Σταθακόπουλος: Πραγματική Ανάλυση
- Γ. Σταύρακας: Σημειώσεις Πραγματικής Ανάλυσης
Σημειώματα Δικαιωμάτων Πνευματικής Ιδιοκτησίας
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Απόστολος Γιαννόπουλος. Πραγματική Ανάλυση. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH4/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».
[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Μετρικοί Χώροι
- Χώροι με νόρμα
- Ορισμός και παραδείγματα
- Ασκήσεις
- Σύγκλιση ακολουθιών και συνέχεια συναρτήσεων
- Σύγκλιση ακολουθιών
- Συνέχεια σε ένα σημείο και αρχή της μεταφοράς
- Ασκήσεις
- Τοπολογία μετρικών χώρων
- Ανοικτά και κλειστά σύνολα
- Εσωτερικό και κλειστή θήκη
- Σχετικώς ανοικτά και κλειστά σύνολα
- Σημεία συσσώρευσης και σύνορο
- Πυκνά σύνολα και διαχωρισιμότητα
- Ασκήσεις
- Συναρτήσεις μεταξύ μετρικών χώρων
- Συνεχείς συναρτήσεις
- Ομοιόμορφα συνεχείς συναρτήσεις
- Ισομετρίες, ομοιομορφισμοί, ισοδύναμες μετρικές
- Βασικά αποτελέσματα για συναρτήσεις σε μετρικούς χώρους
- Ασκήσεις
- Πληρότητα
- Πλήρεις μετρικοί χώροι
- Το θεώρημα του Cantor
- Το θεώρημα κατηγορίας του Baire
- Πλήρωση μετρικού χώρου*
- Το θεώρημα σταθερού σημείου του Banach
- Ασκήσεις
- Συμπάγεια
- Ορισμός της συμπάγειας
- Χαρακτηρισμός της συμπάγειας
- Βασικές ιδιότητες των συμπαγών συνόλων
- Συνεχείς συναρτήσεις σε συμπαγή σύνολα
- Το σύνολο του Cantor
- Ασκήσεις
- Ακολουθίες και σειρές συναρτήσεων
- Ακολουθίες συναρτήσεων: κατά σημείο σύγκλιση
- Ακολουθίες συναρτήσεων: ομοιόμορφη σύγκλιση
- Σειρές Συναρτήσεων
- Ασκήσεις
- Συνεχείς συναρτήσεις σε συμπαγείς μετρικούς χώρους
- Ο χώρος C(K
- Το θεώρημα προσέγγισης του Weierstrass
- Ασκήσεις
Γιαννόπουλος Απόστολος
Θέση : Καθηγητής
Τομέας : Μαθηματικής Ανάλυσης
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Εξοικίωση του διδασκόμενου με τους μετρικούς χώρους, την συνέχεια συναρτήσεων σε μετρικούς χώρους.
Μελέτη:
- Της πληρότητας μετρικών χώρων
- Της συμπάγειας μετρικών χώρων
- Bolzano-Weierstrass και Ολικά Φραγμένα
- Διαχωρισιμότητας
- Συνόλων Cantor
- Απλής και Ομοιόμορφης σύγκλισης ακολουθιών και σειρών συναρτήσεων
- Συνεχών πραγματικών συναρτήσεων σε συμπαγείς μετρικούς χώρους
- Συμπάγειας και ισοσυνέχειας
- Απειροστικός Λογισμός I
- Απειροστικός Λογισμός II
- W. Rudin: Αρχές Μαθηματικής Ανάλυσης
- Κ. Σταθακόπουλος: Πραγματική Ανάλυση
- Γ. Σταύρακας: Σημειώσεις Πραγματικής Ανάλυσης
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Απόστολος Γιαννόπουλος. Πραγματική Ανάλυση. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH4/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».

[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Ορισμός και παραδείγματα
- Χώροι με νόρμα
Λέξεις Κλειδιά: μετρικοί χώροι, χώροι με νόρμα, χώροι πεπερασμένης διάστασης, χώροι ακολουθιών, χώροι συναρτήσεων
- Σύγκλιση ακολουθιών
- Συνέχεια σε ένα σημείο και αρχή της μεταφοράς
Λέξεις Κλειδιά: σύγκλιση ακολουθιών, συγκλίνουσες ακολουθίες, βασικές ακολουθίες και φραγμένες ακολουθίες, υπακολουθίες
- Ανοικτά και κλειστά σύνολα
- Εσωτερικό και κλειστή θήκη
- Σχετικώς ανοιχτά και κλειστά σύνολα
- Σημέια συσσώρευσης και σύνορο
- Πυκνά σύνολα και διαχωρισιμότητα
Λέξεις Κλειδιά: ανοικτά σύνολα, κλειστά σύνολα, εσωτερικό συνόλου, κλειστή θήκη συνόλου, σχετικώς ανοικτά σύνολα, σχετικώς κλειστά σύνολα, σημεία συσσώρευσης και σύνορο, πυκνά υποσύνολα, διαχωρίσιμοι μετρικοί χώροι
- Σημειακή (τοπική) συνέχεια και (ολική) συνέχεια
- Ιδιότητες συνεχών συναρτήσεων
- Ισομετρίες, συναρτήσεις Lipschitz, ομοιόμορφη συνέχεια
Λέξεις Κλειδιά: συνεχείς συναρτήσεις, ομοιόμορφα συνεχείς συναρτήσεις, συναρτήσεις Lipschitz, ισομετρίες, ισοδύναμες μετρικές, ομοιομορφισμοί, το λήμμα του Urysohn, διαμερίσεις της μονάδας, ταλάντωση και σημεία συνέχειας
- Πλήρης μετρικός χώρος (ορισμός, βασικές ιδιότητες, παραδείγματα)
- Θεωρήματα σταθερού σημείου (και εφαρμογές στις διαφορικές εξισώσεις)
- Θεωρήματα Cantor και Baire και εφαρμογές
Λέξεις Κλειδιά: πλήρεις μετρικοί χώροι, θεώρημα Cantor, θεώρημα Baire, πλήρωση μετρικού χώρου, θεώρημα σταθερού σημείου του Banach
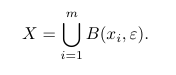
- Ορισμός (με ανοικτές καλύψεις) και βασικές ιδιότητες
- Συνέχεια συναρτήσεων και συμπάγεια
- Χαρακτηρισμοί της συμπάγειας με τη βοήθεια της ιδιότητας Bolzano-Weierstrass και της έννοιας του ολικά φραγμένου
- Πεπερασμένο (καρτεσιανό) γινόμενο συμπαγών μετρικών χώρων
Λέξεις Κλειδιά: συμπάγεια, χαρακτηρισμός της συμπάγειας, βασικές ιδιότητες των συμπαγών συνόλων, συνεχείς συναρτήσεις σε συμπαγή σύνολα, σύνολο Cantor
- Απλή και ομοιόμορφη σύγκλιση (ορισμοί, βασικές ιδιότητες και παραδείγματα)
- Κριτήριο Weierstrass (για την ομοιόμορφη σύγκλιση σειρών συναρτήσεων)
- Ομοιόμορφη σύγκλιση και συνέχεια, ολοκλήρωση και διαφόριση
Λέξεις Κλειδιά: ακολουθίες συναρτήσεων, κατά σημείο σύγκλισης, ομοιόμορφη σύγκλιση, κριτήρια ομοιόμορφης σύγκλισης, σειρές συναρτήσεων
- Θεώρημα προσέγγισης του Weierstrass
- Η δομή του μετρικού χώρου C(X), όπου Χ συμπαγής μετρικός χώρος
- Συμπάγεια και ισοσυνέχεια στον C(X)
- Θεώρημα Ascoli-Arzela και θεώρημα Peano
Λέξεις Κλειδιά: συμπάγεια και ισοσυνέχεια στον C(X), θεώρημα προσέγγισης του Weierstrass, θεώρημα Ascoli-Arzela, θεώρημα Peano
- Ισοπληθικά σύνολα
- Αριθμήσιμα και υπεραριθμήσιμα σύνολα
Λέξεις Κλειδιά: ισοπληθικά σύνολο, ισοπληθικότητα, πεπερασμένα και άπειρα σύνολα, αριθμήσιμα και υπεραριθμήσιμα σύνολα
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -

