Θεωρία Συνόλων
Αθανάσιος Τσαρπαλιάς
Η Θεωρία Συνόλων είναι μία συναρπαστική ζωντανή μαθηματική θεωρία, με τις δικές της βασικές έννοιες, θεμελιακά αποτελέσματα και προβλήματα, και με σημαντικές εφαρμογές σε άλλες θεωρίες. Η Αξιωματική Συνολοθεωρία θεωρείται από πολλούς ως θεμελίωση των μαθηματικών : εικάζεται ότι όλα τα μαθηματικά αντικείμενα είναι πράγματι σύνολα, και ότι οι ιδιότητές τους είναι πορίσματα των λιτών, κομψών αξιωμάτων για τα σύνολα.
Από την “καθαρή” θεωρία συνόλων, οι Σημειώσεις αυτές καλύπτουν τα βασικά αποτελέσματα για “αφηρημένα σύνολα”, το Αξίωμα Επιλογής, υπερπεπερασμένη αναδρομή, πληθικούς και διατακτικούς αριθμούς. Λιγότερο συνηθισμένη είναι η Ενότητα 10 για “σημειοσύνολα”, που περιέχει αποτελέσματα με γνωστές εφαρμογές στην Ανάλυση και εισάγει τον αναγνώστη στο Πρόβλημα του Συνεχούς, κεντρική ερώτηση της συνολοθεωρίας από τα πρώτα της βήματα.
Υπάρχουν πολλές, απλές Ασκήσεις, που ελέγχουν την κατανόηση καινούριων εννοιών αμέσως μετά την εισαγωγή τους. Στο μάθημα παρουσιάζονται μερικές απ' αυτές, για παραδείγματα και οι υπόλοιπες ανατίθενται στους φοιτητές.
Τα Προβλήματα στο τέλος κάθε κεφαλαίου είναι ποικίλης δυσκολίας, και μερικά απ' αυτά καλύπτουν επιπρόσθετη ύλη. Όπως συνηθίζεται, τα πιο δύσκολα από τα προβλήματα σημαδεύονται μ' έναν *.
Λιγότερα
Η Θεωρία Συνόλων είναι μία συναρπαστική ζωντανή μαθηματική θεωρία, με τις δικές της βασικές έννοιες, θεμελιακά αποτελέσματα και προβλήματα, και με σημαντικές εφαρμογές σε άλλες θεωρίες. Η Αξιωματική Συνολοθεωρία θεωρείται από πολλούς ως θεμελίωση των μαθηματικών : εικάζεται ότι όλα τα μαθηματικά αντικείμενα είναι πράγματι σύνολα, και ότι οι ιδιότητές τους είναι πορίσματα των λιτών, κομψών αξιωμάτων για τα σύνολα.
Από την “καθαρή” θεωρία συνόλων, οι Σημειώσεις αυτές καλύπτουν τα βασικά αποτελέσματα για “αφηρημένα σύνολα”, το Αξίωμα Επιλογής, υπερπεπερασμένη αναδρομή, πληθικούς και διατακτικούς αριθμούς. Λιγότερο συνηθισμένη είναι η Ενότητα 10 για “σημειοσύνολα”, που περιέχει αποτελέσματα με γνωστές εφαρμογές στην Ανάλυση και εισάγει τον αναγνώστη στο Πρόβλημα του Συνεχούς, κεντρική ερώτηση της συνολοθεωρίας από τα πρώτα της βήματα.
Υπάρχουν πολλές, απλές Ασκήσεις, που ελέγχουν την κατανόηση καινούριων εννοιών αμέσως μετά την εισαγωγή τους. Στο μάθημα παρουσιάζονται μερικές απ' αυτές, γι
Η Θεωρία Συνόλων είναι μία συναρπαστική ζωντανή μαθηματική θεωρία, με τις δικές της βασικές έννοιες, θεμελιακά αποτελέσματα και προβλήματα, και με σημαντικές εφαρμογές σε άλλες θεωρίες. Η Αξιωματική Συνολοθεωρία θεωρείται από πολλούς ως θεμελίωση των μαθηματικών : εικάζεται ότι όλα τα μαθηματικά αντικείμενα είναι πράγματι σύνολα, και ότι οι ιδιότητές τους είναι πορίσματα των λιτών, κομψών αξιωμάτων για τα σύνολα.
Από την “καθαρή” θεωρία συνόλων, οι Σημειώσεις αυτές καλύπτουν τα βασικά αποτελέσματα για “αφηρημένα σύνολα”, το Αξίωμα Επιλογής, υπερπεπερασμένη αναδρομή, πληθικούς και διατακτικούς αριθμούς. Λιγότερο συνηθισμένη είναι η Ενότητα 10 για “σημειοσύνολα”, που περιέχει αποτελέσματα με γνωστές εφαρμογές στην Ανάλυση και εισάγει τον αναγνώστη στο Πρόβλημα του Συνεχούς, κεντρική ερώτηση της συνολοθεωρίας από τα πρώτα της βήματα.
Υπάρχουν πολλές, απλές Ασκήσεις, που ελέγχουν την κατανόηση καινούριων εννοιών αμέσως μετά την εισαγωγή τους. Στο μάθημα παρουσιάζονται μερικές απ' αυτές, γι
Περίγραμμα

Διδάσκοντες
Αθανάσιος Τσαρπαλιάς
Θέση: Καθηγητής
Ερευνητικά ενδιαφέροντα: Άπειρη Συνδυαστική, Θεωρία Χώρων Banach, Μιγαδική Ανάλυση
Τομέας: Μαθηματικής Ανάλυσης
Τμήμα Μαθηματικών, Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
Περιεχόμενο μαθήματος
- Διαισθητική εισαγωγή των συνόλων
- Αξιωματική θεμελίωση κατά Zermelo-Fraenkel
- Διατακτικοί αριθμοί, πληθάριθμοι
- Αξιώμα επιλογής και ισοδύναμά του
- Υποσύνολα των πραγματικών αριθμών, υπόθεση του συνεχούς, γενικευμένη υπόθεση του συνεχούς
- Κατασκευάσιμα σύνολα
Προτεινόμενα συγγράμματα
Γιάννης Ν. Μοσχοβάκης - “Σημειώσεις στη Συνολοθεωρία” , Εκδόσεις Νεφέλη, 1993.
Μαθησιακοί στόχοι
- Η αξιωματική θεμελίωση της θεωρίας συνόλων, κατά Zermelo-Fraenkel
- Η εξοικείωση με την έννοια του Συστήματος Φυσικών Αριθμών και τα Αξιώματα του Peano
- Η εξοικείωση με το Αξίωμα της Επιλογής και τις ισοδύναμες διατυπώσεις του
- Η κατανόηση της έννοιας του διατακτικού αριθμού
Ομάδα στόχος
Προπτυχιακοί φοιτητές του Τμήματος Μαθηματικών του ΕΚΠΑ, ενδιαφερόμενοι για τις θεματικές περιοχές “Θεωρητικά Μαθηματικά”, “Θεωρητική Πληροφορική”, “Αλγόριθμοι”.
Προαπαιτούμενα
Δεν υπάρχουν προαπαιτούμενα για το μάθημα.
Βιβλιογραφία
- Georg Cantor, “Contributions to the founding of the theory of transfinite numbers”, Dover Publications, New York.
- Jean van Heijenoort, “From Frege to Gödel”, Harvard University Press, Cambridge, 1967.
Αθανάσιος Τσαρπαλιάς
Θέση: Καθηγητής
Ερευνητικά ενδιαφέροντα: Άπειρη Συνδυαστική, Θεωρία Χώρων Banach, Μιγαδική Ανάλυση
Τομέας: Μαθηματικής Ανάλυσης
Τμήμα Μαθηματικών, Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
- Διαισθητική εισαγωγή των συνόλων
- Αξιωματική θεμελίωση κατά Zermelo-Fraenkel
- Διατακτικοί αριθμοί, πληθάριθμοι
- Αξιώμα επιλογής και ισοδύναμά του
- Υποσύνολα των πραγματικών αριθμών, υπόθεση του συνεχούς, γενικευμένη υπόθεση του συνεχούς
- Κατασκευάσιμα σύνολα
Γιάννης Ν. Μοσχοβάκης - “Σημειώσεις στη Συνολοθεωρία” , Εκδόσεις Νεφέλη, 1993.
- Η αξιωματική θεμελίωση της θεωρίας συνόλων, κατά Zermelo-Fraenkel
- Η εξοικείωση με την έννοια του Συστήματος Φυσικών Αριθμών και τα Αξιώματα του Peano
- Η εξοικείωση με το Αξίωμα της Επιλογής και τις ισοδύναμες διατυπώσεις του
- Η κατανόηση της έννοιας του διατακτικού αριθμού
Προπτυχιακοί φοιτητές του Τμήματος Μαθηματικών του ΕΚΠΑ, ενδιαφερόμενοι για τις θεματικές περιοχές “Θεωρητικά Μαθηματικά”, “Θεωρητική Πληροφορική”, “Αλγόριθμοι”.
Δεν υπάρχουν προαπαιτούμενα για το μάθημα.
- Georg Cantor, “Contributions to the founding of the theory of transfinite numbers”, Dover Publications, New York.
- Jean van Heijenoort, “From Frege to Gödel”, Harvard University Press, Cambridge, 1967.
- Η έννοια του συνόλου
- Ιδιότητες των συνόλων
- Πράξεις Boole
- Η έννοια της συνάρτησης
- Σύνθεση συναρτήσεων
Λέξεις κλειδιά: σύνολο, στοιχείο, έκταση, κενό, υποσύνολο, ένωση, τομή, ξένα, συνάρτηση, εικόνα, αντίστροφη, σύνθεση
- Η έννοια της ισοπληθικότητας
- Πεπερασμένα και άπειρα σύνολα
- Αριθμήσιμα και μη αριθμήσιμα σύνολα
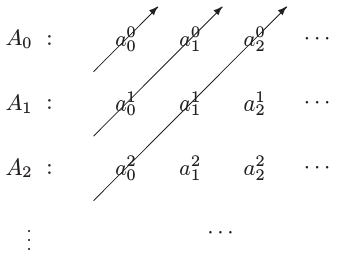
- Η ένωση αριθμήσιμων συνόλων
- Το θεώρημα Cantor για τις δυαδικές ακολουθίες
- Το σύνολο Cantor
- Καρτεσιανό γινόμενο συνόλων
- Το δυναμοσύνολο ενός συνόλου
- Το θεώρημα Schröder-Bernstein
Λέξεις κλειδιά: σύνολο, ισοπληθικά, πεπερασμένο, άπειρο, αριθμήσιμο, υπεραριθμήσιμο, Cantor, καρτεσιανό γινόμενο, δυναμοσύνολο
- Η Γενική Αρχή Συμπερίληψης
- Οριστικές συνθήκες και τελεστές
- Το παράδοξο του Russell
- Η αξιωματική βάση της συνολοθεωρίας
- Αξιώματα για οριστικές συνθήκες και τελεστές
- Η έννοια της κλάσης
Λέξεις κλειδιά: αρχή, συνθήκη, τελεστής, παράδοξο, αξιώματα, κλάση
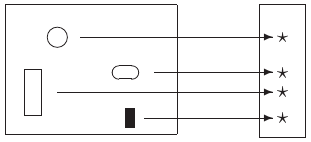
- Η έννοια του διατεταγμένου ζεύγους
- Ξένη ένωση συνόλων
- Η έννοια της διμελούς σχέσης
- Σχέσεις και κλάσεις ισοδυναμίας
- Η έννοια του πληθάριθμου
- Αριθμητική πληθάριθμων
Λέξεις κλειδιά: ζεύγος, διατεταγμένο, ένωση, ξένη, σχέση, διμελής, ισοδυναμία, κλάση, πληθάριθμος
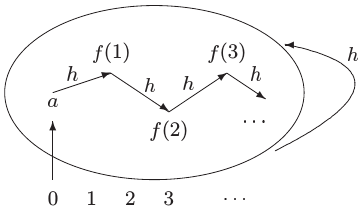
- Σύστημα φυσικών αριθμών
- Το θεώρημα αναδρομής
- Το θεώρημα Schröder-Bernstein
- Μερική και ολική διάταξη
- Η έννοια της καλής διάταξης
- Η αρχή του περιστερεώνα
Λέξεις κλειδιά: σύστημα, φυσικός αριθμός, Peano, αναδρομή, διάταξη
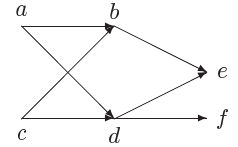
- Μερικά διατεταγμένοι χώροι
- Άνω φράγμα και ελάχιστο άνω φράγμα
- Η έννοια της μερικής συνάρτησης
- Η έννοια της αλυσίδας
- Μονοτονικές συναρτήσεις
- Το συνεχές θεώρημα ελάχιστου σταθερού σημείου
- Συνεχείς συναρτήσεις
Λέξεις κλειδιά: χώρος, μερική διάταξη, άνω φράγμα, supremum, αλυσίδα, συνάρτηση, μονοτονική, συνεχής, σταθερό σημείο
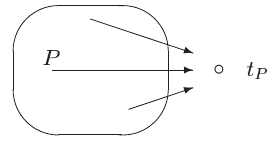
- Καλά διατάξιμα σύνολα
- Επόμενα και οριακά σημεία
- Ισομορφικοί χώροι
- Το θεώρημα υπερπεπερασμένης επαγωγής
- Το θεώρημα υπερπεπερασμένης αναδρομής
- Συγκρισιμότητα καλά διατεταγμένων χώρων
- Το θεώρημα Hartogs
- Το θεώρημα σταθερού σημείου του Zermelo
Λέξεις κλειδιά: καλή διάταξη, σημείο, επόμενο, οριακό, χώρος, ισομορφικός, Hartogs, Zermelo, αρχικό τμήμα, επεκτατική απεικόνιση
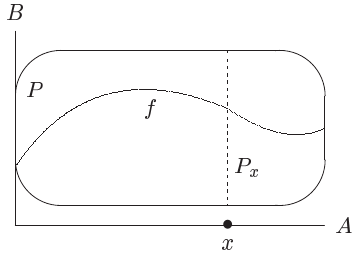
- Το αξίωμα επιλογής
- Ισοδύναμες διατυπώσεις του αξιώματος επιλογής
- Η αξιωματική θεωρία ZDC
- Συνέπεια και ανεξαρτησία του αξιώματος επιλογής
Λέξεις κλειδιά: επιλογή, αξίωμα, καλή διάταξη, λήμμα Zorn, αλυσίδα
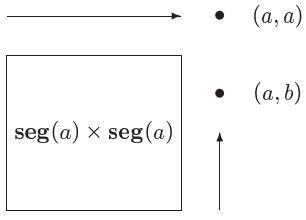
- Δέντρα σε σύνολα
- Το θεώρημα βεντάλιας
- Η έννοια της άριστης διάταξης
- Το θεώρημα του König
- Η έννοια της ομοτελικότητας
Λέξεις κλειδιά: πληθική αριθμητική, Dedekind, δέντρο, λήμμα König, άριστη διάταξη, κανόνες απορρόφησης, ομοτελικότητα
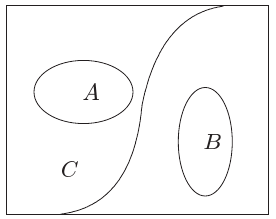
- Η δομή του χώρου Baire
- Aνοικτά και κλειστά σημειοσύνολα
- Tο θεώρημα Cantor-Bendixson
- Συμπαγή σημειοσύνολα
- Το θεώρημα τέλειου συνόλου
- Το θεώρημα διαχωρισμού
- Το θεώρημα Suslin
Λέξεις κλειδιά: χώρος, Baire, σημειοσύνολο, ανοικτό, κλειστό, αναλυτικό Suslin, συμπαγές, Borel
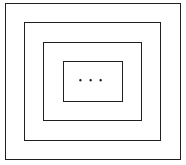
- Το αξίωμα αντικατάστασης
- Η έννοια του μεταβατικού συνόλου
- Το θεώρημα μεταβατικής κλειστότητας
- Ο ελάχιστος κόσμος του Zermelo
Λέξεις κλειδιά: αντικατάσταση, αξίωμα, τελεστής, συνθήκη, αναδρομή, κλάση, μεταβατική, κλειστότητα, κόσμος Zermelo
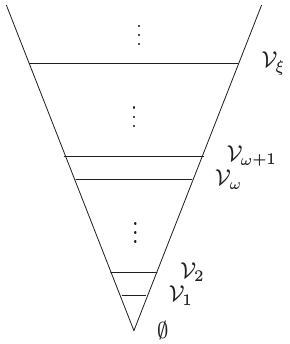
- Η έννοια του διατακτικού αριθμού
- Ιδιότητες των διατακτικών αριθμών
- Σύγκριση διατακτικών αριθμών
- Επόμενοι και οριακοί διατακτικοί αριθμοί
- Πληθάριθμοι του Von Neumann
Λέξεις κλειδιά: αριθμός, διατακτικός, Von Neumann, σύγκριση, διάταξη, επόμενος, οριακός, πληθάριθμος
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -