Υπολογιστική Άλγεβρα (MATH117)
Ευάγγελος Ράπτης
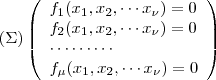
Βασικός σκοπός του μαθήματος είναι να διαπραγματευθεί τις μαθηματικές μεθόδους και δέες(κυρίωςαλγεβρικές) για να λυθεί ένα σύστημα (Σ) με μ πολυωνυμικές εξισώσεις και ν μεταβλητές. Η αντιμετώπιση αυτή οδηγεί σε ερωτήματα για το σύνολο λύσεων του Σ. Αποδεικνύεται ότι το σύνολο λυσεων εξαρτάται στην πραγματικότητα από το ιδεώδες των πολυωνύμων στον αντίστοιχο δακτύλιο πολυωνύμων με πολλές μεταβλητές. Ιδέες γνωστές από τη Γραμμική άλγεβρα (π.χ η έννοια της βάσης) εμφανίζονται και αναπτύσσονται. Σημαντικό ρόλο παίζει εδώ η έννοια της βάσης Groebner. Επιπλέον μελετώνται οι αλγόριθμοι για την αντιμετώπιση των παραπάνω προβλημάτων. Τα παραδείγματα και οι εφαρμογές προέρχονται από την Τεχνητή νοημοσύνη, την Ρομποτική και την Βιολογία.
Λιγότερα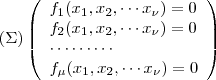
Βασικός σκοπός του μαθήματος είναι να διαπραγματευθεί τις μαθηματικές μεθόδους και δέες(κυρίωςαλγεβρικές) για να λυθεί ένα σύστημα (Σ) με μ πολυωνυμικές εξισώσεις και ν μεταβλητές. Η αντιμετώπιση αυτή οδηγεί σε ερωτήματα για το σύνολο λύσεων του Σ. Αποδεικνύεται ότι το σύνολο λυσεων εξαρτάται στην πραγματικότητα από το ιδεώδες των πολυωνύμων στον αντίστοιχο δακτύλιο πολυωνύμων με πολλές μεταβλητές. Ιδέες γνωστές από τη Γραμμική άλγεβρα (π.χ η έννοια της βάσης) εμφανίζονται και αναπτύσσονται. Σημαντικό ρόλο παίζει εδώ η έννοια της βάσης Groebner. Επιπλέον μελετώνται οι αλγόριθμοι για την αντιμετώπιση των παραπάνω προβλημάτων. Τα παραδείγματα και οι εφαρμογές προέρχονται από την Τεχνητή νοημοσύνη, την Ρομποτική και την Βιολογία.
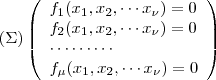
Βασικός σκοπός του μαθήματος είναι να διαπραγματευθεί τις μαθηματικές μεθόδους και δέες(κυρίωςαλγεβρικές) για να λυθεί ένα σύστημα (Σ) με μ πολυωνυμικές εξισώσεις και ν μεταβλητές. Η αντιμετώπιση αυτή οδηγεί σε ερωτήματα για το σύνολο λύσεων του Σ. Αποδεικνύεται ότι το σύνολο λυσεων εξαρτάται στην πραγματικότητα από το ιδεώδες των πολυωνύμων στον αντίστοιχο δακτύλιο πολυωνύμων με πολλές μεταβλητές. Ιδέες γνωστές από τη Γραμμική άλγεβρα (π.χ η έννοια της βάσης) εμφανίζονται και αναπτύσσονται. Σημαντικό ρόλο παίζει εδώ η έννοια της βάσης Groebner. Επιπλέον μελετώνται οι αλγόριθμοι για την αντιμετώπιση των παραπάνω προβλημάτων. Τα παραδείγματα και οι εφαρμογές προέρχονται από την Τεχνητή νοημοσύνη, την Ρομποτική και την Βιολογία.
Περίγραμμα
Περιεχόμενο μαθήματος
Διδακτέα ύλη:
- Πολυώνυμα πολλών μεταβλητών.
- Σύστημα πολυωνυμικών εξισώσεων πολλών μεταβλητών.
- Βάσεις Groebner, θεώρημα βάσης του Hilbert.
- Ιδιότητες βάσεων Groebner και αλγόριθμοι επίλυσης συστημάτων πολυωνυμικών εξισώσεων.
- Βασικές αρχές της Ρομποτικής.
Εξάσκηση στον υπολογιστή στα παραπάνω θέματα.
Μαθησιακοί στόχοι
Βασικός σκοπός του μαθήματος είναι να διαπραγματευθεί τις μαθηματικές μεθόδους και δέες(κυρίωςαλγεβρικές) για να λυθεί ένα σύστημα (Σ) με μ πολυωνυμικές εξισώσεις και ν μεταβλητές. Η αντιμετώπιση αυτή οδηγεί σε ερωτήματα για το σύνολο λύσεων του Σ. Αποδεικνύεται ότι το σύνολο λυσεων εξαρτάται στην πραγματικότητα από το ιδεώδες των πολυωνύμων στον αντίστοιχο δακτύλιο πολυωνύμων με πολλές μεταβλητές. Ιδέες γνωστές από τη Γραμμική άλγεβρα (π.χ η έννοια της βάσης) εμφανίζονται και αναπτύσσονται. Σημαντικό ρόλο παίζει εδώ η έννοια της βάσης Groebner .Επιπλέον μελετώνται οι αλγόριθμοι για την αντιμετώπιση των παραπάνω προβλημάτων. Τα παραδείγματα και οι εφαρμογές προέρχονται από την Τεχνητή νοημοσύνη, την Ρομποτική και την Βιολογία
Βιβλιογραφία
Βοηθήματα:
- Θα υπάρχει συνεχής ροή ηλεκτρονικών σημειώσεων.
- Δύο είναι τα κύρια ξενόγλωσσα βιβλία χρήσιμα για το μάθημα:
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea ΤαβιβλίααυτάυπάρχουνστηνβιβλιοθήκητουΤμήματος
3. Πολλές χρήσιμες πληροφορίες θα βρείτε και στις ηλεκτρονικές διεθύνσεις που θα δημοσιεύονται.
Μέθοδοι διδασκαλίας
Διδασκαλία καθ΄ έδρας και συμπληρωματική-ενισχυτική εκπαίδευση μέσω ασύγχρονης πλατφόρμας.
Μέθοδοι αξιολόγησης
Ο τρόπος αξιολόγησης/εξέτασης θα γίνει ως εξής;
Κατά τη διάρκεια του εξαμήνου θα δοθούν 10 εργασίες. Πλήρης ανάπτυξη και σωστή απάντηση της κάθε μίας βαθμολογείται με 10 μονάδα (στις 100). Σύνολο 100 μονάδες. Επίσης ενδεχομένως θα υπάρξει και προφορική εξέταση
Προαπαιτούμενα
Γραμμική άλγεβρα, Βασική άλγεβρα
Διδάσκοντες
Ράπτης Ευάγγελος
Καθηγητής
Ερευνητικά Ενδιαφέροντα : Θεωρία ομάδων, Κρυπτογραφία, Υπολογιστική άλγεβρα
e-mail : eraptis@math.uoa.gr
Προσωπική Ιστοσελίδα:
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών.
Undergraduate students of University of Athens Department of Mathematics
Προτεινόμενα συγγράμματα
Βοηθήματα:
- Θα υπάρχει συνεχής ροή ηλεκτρονικών σημειώσεων.
- Δύο είναι τα κύρια ξενόγλωσσα βιβλία χρήσιμα για το μάθημα:
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea
Τα βιβλία αυτά υπάρχουν στην βιβλιοθήκη του Τμήματος
3. Πολλές χρήσιμες πληροφορίες θα βρείτε και στις ηλεκτρονικές διεθύνσεις που θα δημοσιεύονται.
Διδακτέα ύλη:
- Πολυώνυμα πολλών μεταβλητών.
- Σύστημα πολυωνυμικών εξισώσεων πολλών μεταβλητών.
- Βάσεις Groebner, θεώρημα βάσης του Hilbert.
- Ιδιότητες βάσεων Groebner και αλγόριθμοι επίλυσης συστημάτων πολυωνυμικών εξισώσεων.
- Βασικές αρχές της Ρομποτικής.
Εξάσκηση στον υπολογιστή στα παραπάνω θέματα.
Βασικός σκοπός του μαθήματος είναι να διαπραγματευθεί τις μαθηματικές μεθόδους και δέες(κυρίωςαλγεβρικές) για να λυθεί ένα σύστημα (Σ) με μ πολυωνυμικές εξισώσεις και ν μεταβλητές. Η αντιμετώπιση αυτή οδηγεί σε ερωτήματα για το σύνολο λύσεων του Σ. Αποδεικνύεται ότι το σύνολο λυσεων εξαρτάται στην πραγματικότητα από το ιδεώδες των πολυωνύμων στον αντίστοιχο δακτύλιο πολυωνύμων με πολλές μεταβλητές. Ιδέες γνωστές από τη Γραμμική άλγεβρα (π.χ η έννοια της βάσης) εμφανίζονται και αναπτύσσονται. Σημαντικό ρόλο παίζει εδώ η έννοια της βάσης Groebner .Επιπλέον μελετώνται οι αλγόριθμοι για την αντιμετώπιση των παραπάνω προβλημάτων. Τα παραδείγματα και οι εφαρμογές προέρχονται από την Τεχνητή νοημοσύνη, την Ρομποτική και την Βιολογία
Βοηθήματα:
- Θα υπάρχει συνεχής ροή ηλεκτρονικών σημειώσεων.
- Δύο είναι τα κύρια ξενόγλωσσα βιβλία χρήσιμα για το μάθημα:
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea ΤαβιβλίααυτάυπάρχουνστηνβιβλιοθήκητουΤμήματος
3. Πολλές χρήσιμες πληροφορίες θα βρείτε και στις ηλεκτρονικές διεθύνσεις που θα δημοσιεύονται.
Διδασκαλία καθ΄ έδρας και συμπληρωματική-ενισχυτική εκπαίδευση μέσω ασύγχρονης πλατφόρμας.
Ο τρόπος αξιολόγησης/εξέτασης θα γίνει ως εξής;
Κατά τη διάρκεια του εξαμήνου θα δοθούν 10 εργασίες. Πλήρης ανάπτυξη και σωστή απάντηση της κάθε μίας βαθμολογείται με 10 μονάδα (στις 100). Σύνολο 100 μονάδες. Επίσης ενδεχομένως θα υπάρξει και προφορική εξέταση
Γραμμική άλγεβρα, Βασική άλγεβρα
Ράπτης Ευάγγελος
Καθηγητής
Ερευνητικά Ενδιαφέροντα : Θεωρία ομάδων, Κρυπτογραφία, Υπολογιστική άλγεβρα
e-mail : eraptis@math.uoa.gr
Προσωπική Ιστοσελίδα:
|
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών. |
|
Undergraduate students of University of Athens Department of Mathematics |
Βοηθήματα:
- Θα υπάρχει συνεχής ροή ηλεκτρονικών σημειώσεων.
- Δύο είναι τα κύρια ξενόγλωσσα βιβλία χρήσιμα για το μάθημα:
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea
Τα βιβλία αυτά υπάρχουν στην βιβλιοθήκη του Τμήματος
3. Πολλές χρήσιμες πληροφορίες θα βρείτε και στις ηλεκτρονικές διεθύνσεις που θα δημοσιεύονται.
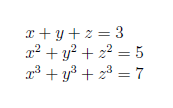
Εισαγωγή. Στο δρόμο για έναν ορισμό. Ασκήσεις και προβληματισμοί.
Λέξεις – κλειδιά: Πολυωνυμικές σχέσεις, Σύνολο Υποθέσεων, Σύνολο συμπερασμάτων
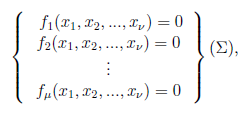
Τα συστήματα. Υποδείξεις για ευρύτερη μελέτη. Άσκηση. Υποδείξεις για την παραπάνω άσκηση.
Λέξεις – κλειδιά: Σύστημα μ εξισώσεων με ν αγνώστους
Έρευνα στο διαδίκτυο. Εξίσωση τρίτου βαθμού-μέθοδος Cardano. Ασκήσεις και προβληματισμοί. Σκέψεις για επίλυση ενός συστήματος με δύο εξισώσεις τρίτου βαθμού.
Λέξεις – κλειδιά: Μέθοδος Cardano
Εξίσωση τετάρτου βαθμού. Έρευνα στο internet. Επίλυση με ριζικά. Η δυστυχία του να μην υπάρχει αλγόριθμος. Πάντα υπάρχει ελπίδα. Σχετικά με τους κοινούς παράγοντες. Η μέθοδος με τον Μέγιστο κοινό Διαιρέτη. Η ορίζουσα Sylvester.
Λέξεις – κλειδιά: Επίλυση με ριζικά, κοινός παράγοντας, μέγιστος κοινός διαιρέτης, ορίζουσα Sylvester
Γενικά για τον δακτύλιο των πολυωνύμων. Προαιρετική άσκηση για εξάσκηση
Λέξεις – κλειδιά: Δακτύλιος πολυωνύμων
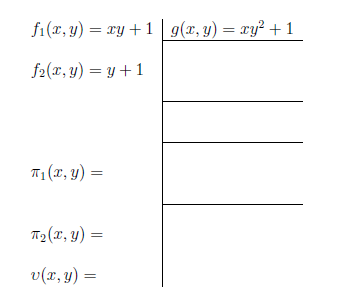
Γενικά. Βήματα διαίρεσης. Παράδειγμα διαίρεσης στον δακτύλιο F[x,y]. Παράδειγμα διαίρεσης στον δακτύλιο F[x,y,z]. Σχόλια πάνω στον αλγόριθμο της διαίρεσης πολυωνύμων πολλών μεταβλητών. Η λεξικογραφική διάταξη. Πηλίκο και υπόλοιπο. Ασκήσεις.
Λέξεις – κλειδιά: Ο αλγόριθμος της διαίρεσης, δακτύλιος F[x,y], λεξικογραφική, ενδιάμεσο υπόλοιπο
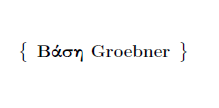
Ιδεώδη μονονύμων. Ασκήσεις.
Λέξεις – κλειδιά: Ιδεώδη μονονύμων, βάση Groebner
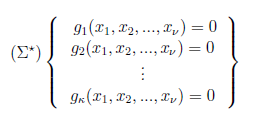
Ξανά το σύστημα. Ευρύτερη μελέτη. Άσκήσεις.
Λέξεις – κλειδιά: Πολυωνυμικός συνδυασμός, γραμμικό συνδυασμό διανυσμάτων
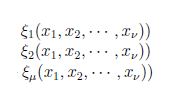
Επαναλήψεις σκέψεις σχόλια. Πολυωνυμικοί συνδυασμοί. Βάσεις Groebner. Χαλαρή μελέτη χωρίς προθεσμίες.
Λέξεις – κλειδιά: Ιδεώδες, πεπερασμένο παραγόμενο
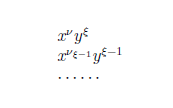
Τρίτο μέρος. Η περίπτωση του δακτυλίου πολυωνύμων μιας μεταβλητής. Η περίπτωση του δακτυλίου πολυωνύμων δύο μεταβλητών.
Λέξεις – κλειδιά: Κύριο ιδεώδες
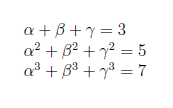
Γενικά. Ελαχιστοποιημένες και ανηγμένες. Βάσεις Groebner. Ταυτότητες στο Γυμνάσιο-Λύκειο. Και άλλα για πολυωνυμικές ταυτότητες.
Λέξεις – κλειδιά: Ανηγμένες βάσεις Groebner, θεώρημα Schwartz, Zippel, Tarski, Seidenberg
Ο αλγόριθμος του Buchberger. Ασκήσεις. Τεχνητή νοημοσύνη. Το θεώρημα βάσης του Hilbert. Αυτόματη απόδειξη Γεωμετρικών Θεωρημάτων. Τεχνητή νοημοσύνη και Γραμμική άλγεβρα.
Λέξεις – κλειδιά: Ελάχιστο κοινό πολλαπλάσιο, S-πολυώνυμο, τεχνητή νοημοσύνη, γραμμική άλγεβρα
Ασκήσεις
Λέξεις – κλειδιά: Κινηματικό πρόβλημα
Ανοικτό Ακαδ. Μάθημα
Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -
