Άλγεβρα
Ευάγγελος Ράπτης
Το μεταπτυχιακό μάθημα “Άλγεβρα” προσφέρεται ως μάθημα επιλογής στο διαπανεπιστημιακό μεταπτυχιακό πρόγραμμα “Διδακτική των Μαθηματικών”.
Στην πρώτη ενότητα του μαθήματος μελετώνται οι πολυωνυμικές σχέσεις για πολυώνυμα μίας μεταβλητής έως και τετάρτου βαθμού. Εισάγονται έννοιες από τη Θεωρία Ομάδων και τη Θεωρία Galois και παρουσιάζεται η ορίζουσα του Sylvester.
Στη δεύτερη ενότητα παρουσιάζεται ο αλγόριθμος της διαίρεσης για πολυώνυμα πολλών μεταβλητών.
Στην τρίτη ενότητα εισάγεται η έννοια της βάσης Groebner ενός ιδεώδους.
Στην τέταρτη ενότητα παρουσιάζεται ο αλγόριθμος του Buchberger για την εύρεση μίας βάσης Groebner.
Λιγότερα
Το μεταπτυχιακό μάθημα “Άλγεβρα” προσφέρεται ως μάθημα επιλογής στο διαπανεπιστημιακό μεταπτυχιακό πρόγραμμα “Διδακτική των Μαθηματικών”.
Στην πρώτη ενότητα του μαθήματος μελετώνται οι πολυωνυμικές σχέσεις για πολυώνυμα μίας μεταβλητής έως και τετάρτου βαθμού. Εισάγονται έννοιες από τη Θεωρία Ομάδων και τη Θεωρία Galois και παρουσιάζεται η ορίζουσα του Sylvester.
Στη δεύτερη ενότητα παρουσιάζεται ο αλγόριθμος της διαίρεσης για πολυώνυμα πολλών μεταβλητών.
Στην τρίτη ενότητα εισάγεται η έννοια της βάσης Groebner ενός ιδεώδους.
Στην τέταρτη ενότητα παρουσιάζεται ο αλγόριθμος του Buchberger για την εύρεση μίας βάσης Groebner.
Το μεταπτυχιακό μάθημα “Άλγεβρα” προσφέρεται ως μάθημα επιλογής στο διαπανεπιστημιακό μεταπτυχιακό πρόγραμμα “Διδακτική των Μαθηματικών”.
Στην πρώτη ενότητα του μαθήματος μελετώνται οι πολυωνυμικές σχέσεις για πολυώνυμα μίας μεταβλητής έως και τετάρτου βαθμού. Εισάγονται έννοιες από τη Θεωρία Ομάδων και τη Θεωρία Galois και παρουσιάζεται η ορίζουσα του Sylvester.
Στη δεύτερη ενότητα παρουσιάζεται ο αλγόριθμος της διαίρεσης για πολυώνυμα πολλών μεταβλητών.
Στην τρίτη ενότητα εισάγεται η έννοια της βάσης Groebner ενός ιδεώδους.
Στην τέταρτη ενότητα παρουσιάζεται ο αλγόριθμος του Buchberger για την εύρεση μίας βάσης Groebner.
Περίγραμμα

Περιεχόμενο μαθήματος
- Συμμετρίες και συμμετρικές ομάδες
- Κατάταξη των ισομετριών του επιπέδου και του χώρου
- Δράσεις ομάδων σε σύνολα
- Θεωρήματα Sylow
- Επιλύσιμες ομάδες
- Πολυώνυμα και θεωρία Galois
- Κατασκευές με κανόνα και διαβήτη
Μαθησιακοί στόχοι
- Η κατανόηση της μετάβασης από ένα σύνολο υποθέσεων σε ένα σύνολο συμπερασμάτων, που διατυπώνονται με πολυώνυμα.
- Η εξοικείωση με τις αλγεβρικές δομές του δακτυλίου των πολυωνύμων και του ιδεώδους ενός δακτυλίου.
- Η χρήση υπολογιστικών πακέτων για την επίλυση αλγεβρικών προβλημάτων.
- Η εξοικείωση με τη Θεωρία Galois για την απόδειξη της επιλυσιμότητας πολυωνύμων με χρήση ριζικών.
- Η εξοικείωση με τον αλγόριθμο της διαίρεσης για πολυώνυμα πολλών μεταβλητών.
- Η εξοικείωση με τις βάσεις Groebner ενός ιδεώδους και με τις μεθόδους προσδιορισμού μίας ανηγμένης βάσης Groebner.
- Η κατανόηση του αλγόριθμου Buchberger για τον προσδιορισμό μίας βάσης Groebner ενός ιδεώδους.
Προτεινόμενα συγγράμματα
Προτείνονται τα παρακάτω ξενόγλωσσα συγγράμματα :
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea
Τα βιβλία αυτά υπάρχουν στην βιβλιοθήκη του Τμήματος Μαθηματικών του ΕΚΠΑ.
Προαπαιτούμενα
Γραμμική Άλγεβρα, Βασική Άλγεβρα
Ομάδα στόχος
Μεταπτυχιακοί φοιτητές του διαπανεπιστημιακού προγράμματος σπουδών “Διδακτική και Μεθοδολογία των Μαθηματικών”.
Διδάσκοντες
- Συμμετρίες και συμμετρικές ομάδες
- Κατάταξη των ισομετριών του επιπέδου και του χώρου
- Δράσεις ομάδων σε σύνολα
- Θεωρήματα Sylow
- Επιλύσιμες ομάδες
- Πολυώνυμα και θεωρία Galois
- Κατασκευές με κανόνα και διαβήτη
- Η κατανόηση της μετάβασης από ένα σύνολο υποθέσεων σε ένα σύνολο συμπερασμάτων, που διατυπώνονται με πολυώνυμα.
- Η εξοικείωση με τις αλγεβρικές δομές του δακτυλίου των πολυωνύμων και του ιδεώδους ενός δακτυλίου.
- Η χρήση υπολογιστικών πακέτων για την επίλυση αλγεβρικών προβλημάτων.
- Η εξοικείωση με τη Θεωρία Galois για την απόδειξη της επιλυσιμότητας πολυωνύμων με χρήση ριζικών.
- Η εξοικείωση με τον αλγόριθμο της διαίρεσης για πολυώνυμα πολλών μεταβλητών.
- Η εξοικείωση με τις βάσεις Groebner ενός ιδεώδους και με τις μεθόδους προσδιορισμού μίας ανηγμένης βάσης Groebner.
- Η κατανόηση του αλγόριθμου Buchberger για τον προσδιορισμό μίας βάσης Groebner ενός ιδεώδους.
Προτείνονται τα παρακάτω ξενόγλωσσα συγγράμματα :
- Ideals,Varieties, and Algorithms των D.Cox, J.Little, D. O'Shea
- Using algebraic Geometry των D.Cox, J.Little, D. O'Shea
Τα βιβλία αυτά υπάρχουν στην βιβλιοθήκη του Τμήματος Μαθηματικών του ΕΚΠΑ.
Γραμμική Άλγεβρα, Βασική Άλγεβρα
Μεταπτυχιακοί φοιτητές του διαπανεπιστημιακού προγράμματος σπουδών “Διδακτική και Μεθοδολογία των Μαθηματικών”.
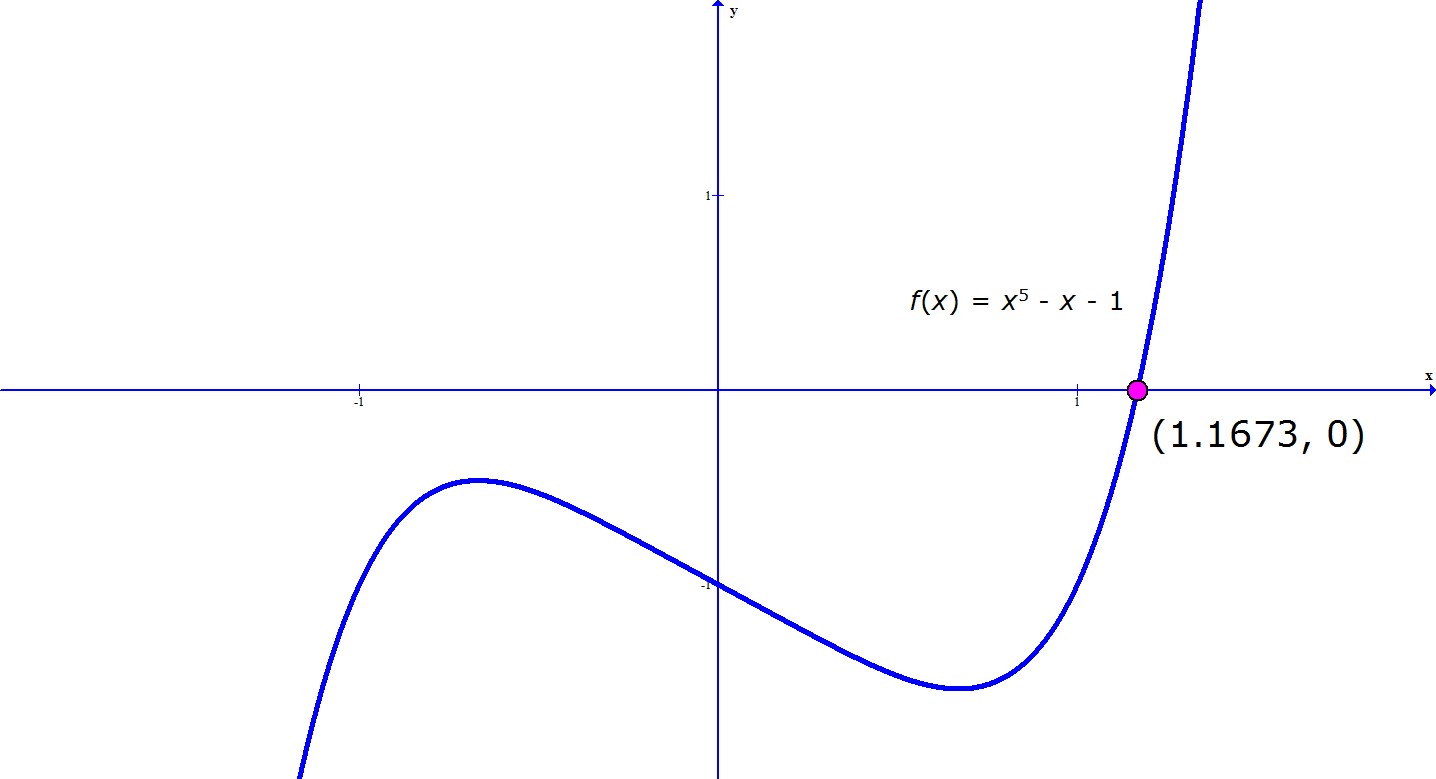
- Πολυωνυμικές σχέσεις και ταυτότητες
- Πολυώνυμα μίας μεταβλητής τρίτου και τετάρτου βαθμού
- Έννοιες της Θεωρίας Ομάδων
- Τα Θεωρήματα Sylow
- Έννοιες από τη Θεωρία Galois
- Κατασκευές με κανόνα και διαβήτη
- Ισομετρίες
Λέξεις κλειδιά: πολυώνυμα, σχέσεις, ταυτότητες, ομάδες, συμμετρίες, ισομετρίες, Sylow, Galois, κατασκευές, κανόνα, διαβήτη
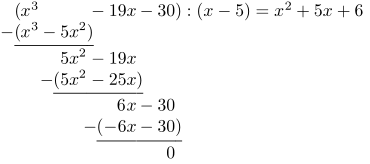
- Εξαγωγή συμπερασμάτων από σύνολο υποθέσεων
- Ταυτότητες
- Ο δακτύλιος των πολυωνύμων
- Διαίρεση πολυωνύμων
- Ο αλγόριθμος της διαίρεσης
- Η λεξικογραφική διάταξη
Λέξεις κλειδιά: πολυώνυμα, ταυτότητες, δακτύλιος, διαίρεση, αλγόριθμος, λεξικογραφική, διάταξη
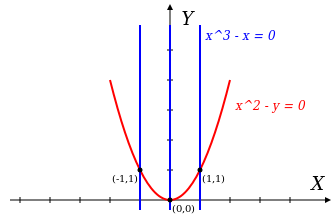
- Η έννοια του ιδεώδους ενός δακτυλίου
- Bάση Groebner ενός ιδεώδους
- H έννοια της ανηγμένης βάσης Groebner
Λέξεις κλειδιά: δακτύλιος, ιδεώδες, βάση Groebner, ανηγμένη
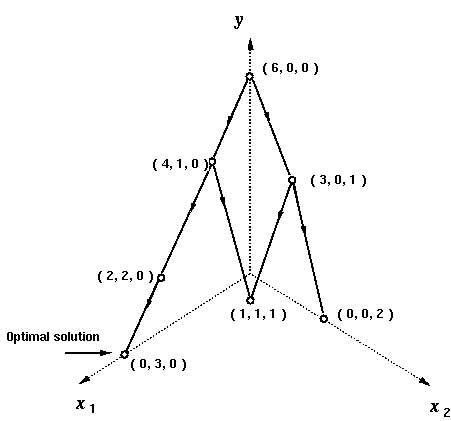
- Η έννοια του S-πολυωνύμου
- Ο αλγόριθμος του Buchberger
- Εφαρμογές στη Γεωμετρία
- Το θεώρημα βάσης του Hilbert
- Αυτόματη απόδειξη γεωμετρικών θεωρημάτων
Λέξεις κλειδιά: S-πολυώνυμο, αλγόριθμος, Buchberger, εφαρμογές, Γεωμετρία, Hilbert, αυτόματη απόδειξη
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -

