Θεωρία Τελεστών
Αριστείδης Κατάβολος
Το μεταπτυχιακό μάθημα “Θεωρία Τελεστών” προσφέρεται ως μάθημα επιλογής στους φοιτητές του Μεταπτυχιακού Προγράμματος Σπουδών στα “Θεωρητικά Μαθηματικά”.
Στην πρώτη ενότητα του μαθήματος γίνεται συνοπτική επισκόπηση στοιχείων για τους χώρους που είναι εφοδιασμένοι με νόρμα και τους χώρους Hilbert.
Στη δεύτερη ενότητα μελετώνται ειδικές κατηγορίες (φραγμένων) τελεστών σ' ένα χώρο Hilbert και εισάγεται η έννοια του αναλλοίωτου υποχώρου.
Στην τρίτη ενότητα παρουσιάζεται μία εισαγωγή για το Φασματικό θεώρημα σε χώρους πεπερασμένης διάστασης, προετοιμάζοντας την μελέτη για τους απειροδιάστατους χώρους.
Στην τέταρτη ενότητα μελετάται η έννοια του φάσματος ενός τελεστή και ειδικότερα ενός αυτοσυζυγούς τελεστή.
Στην πέμπτη ενότητα μελετώνται οι συνεχείς συναρτήσεις ενός αυτοσυζυγούς τελεστή (ο συναρτησιακός λογισμός, η τετραγωνική ρίζα θετικού τελεστή και η πολική αναπαράσταση).
Στην έκτη ενότητα παρουσιάζεται και αποδεικνύεται το Φασματικό θεώρημα για αυτοσυζυγείς τελεστές.
Στην έβδομη ενότητα παρουσιάζεται η δεύτερη μορφή του Φασματικού θεωρήματος, μέσω της έννοιας της ολοκλήρωσης ως προς φασματικό μέτρο. Μελετώνται επίσης η έννοια της *-αναπαράστασης και οι συνεχείς συναρτήσεις ενός φυσιολογικού τελεστή. Ακόμη, παρουσιάζεται το Φασματικό θεώρημα για φυσιολογικούς τελεστές και μία επέκταση του συναρτησιακού λογισμού.
Στην όγδοη ενότητα μελετώνται οι τοπολογίες στο χώρο Β(Η) των τελεστών σ᾽ένα χώρο Hilbert H, εισάγονται οι έννοιες της ισχυρής και της ασθενούς τοπολογίας τελεστών και μελετάται ο χώρος Β(Η) ως δυϊκός χώρος Banach.
Τέλος, στην ένατη ενότητα μελετώνται οι Αβελιανές άλγεβρες von Neumann, παρουσιάζεται και αποδεικνύεται το θεώρημα von Neumann, ενώ αποδεικνύεται ότι κάθε μεγιστική αβελιανή αυτοσυζυγής υπάλγεβρα (masa) που δρά σε διαχωρίσιμο χώρο είναι ισοδύναμη με την πολλαπλασιαστική άλγεβρα ενός χώρου μέτρου.
ΛιγότεραΤο μεταπτυχιακό μάθημα “Θεωρία Τελεστών” προσφέρεται ως μάθημα επιλογής στους φοιτητές του Μεταπτυχιακού Προγράμματος Σπουδών στα “Θεωρητικά Μαθηματικά”.
Στην πρώτη ενότητα του μαθήματος γίνεται συνοπτική επισκόπηση στοιχείων για τους χώρους που είναι εφοδιασμένοι με νόρμα και τους χώρους Hilbert.
Στη δεύτερη ενότητα μελετώνται ειδικές κατηγορίες (φραγμένων) τελεστών σ' ένα χώρο Hilbert και εισάγεται η έννοια του αναλλοίωτου υποχώρου.
Στην τρίτη ενότητα παρουσιάζεται μία εισαγωγή για το Φασματικό θεώρημα σε χώρους πεπερασμένης διάστασης, προετοιμάζοντας την μελέτη για τους απειροδιάστατους χώρους.
Στην τέταρτη ενότητα μελετάται η έννοια του φάσματος ενός τελεστή και ειδικότερα ενός αυτοσυζυγούς τελεστή.
Στην πέμπτη ενότητα μελετώνται οι συνεχείς συναρτήσεις ενός αυτοσυζυγούς τελεστή (ο συναρτησιακός λογισμός, η τετραγωνική ρίζα θετικού τελεστή και η πολική αναπαράσταση).
Στην έκτη ενότητα παρουσιάζεται και αποδεικνύεται το Φασματικό θεώρημα για αυτοσυζυγείς τελεστές.
Στην έβδομη ενότητ
Το μεταπτυχιακό μάθημα “Θεωρία Τελεστών” προσφέρεται ως μάθημα επιλογής στους φοιτητές του Μεταπτυχιακού Προγράμματος Σπουδών στα “Θεωρητικά Μαθηματικά”.
Στην πρώτη ενότητα του μαθήματος γίνεται συνοπτική επισκόπηση στοιχείων για τους χώρους που είναι εφοδιασμένοι με νόρμα και τους χώρους Hilbert.
Στη δεύτερη ενότητα μελετώνται ειδικές κατηγορίες (φραγμένων) τελεστών σ' ένα χώρο Hilbert και εισάγεται η έννοια του αναλλοίωτου υποχώρου.
Στην τρίτη ενότητα παρουσιάζεται μία εισαγωγή για το Φασματικό θεώρημα σε χώρους πεπερασμένης διάστασης, προετοιμάζοντας την μελέτη για τους απειροδιάστατους χώρους.
Στην τέταρτη ενότητα μελετάται η έννοια του φάσματος ενός τελεστή και ειδικότερα ενός αυτοσυζυγούς τελεστή.
Στην πέμπτη ενότητα μελετώνται οι συνεχείς συναρτήσεις ενός αυτοσυζυγούς τελεστή (ο συναρτησιακός λογισμός, η τετραγωνική ρίζα θετικού τελεστή και η πολική αναπαράσταση).
Στην έκτη ενότητα παρουσιάζεται και αποδεικνύεται το Φασματικό θεώρημα για αυτοσυζυγείς τελεστές.
Στην έβδομη ενότητ
Περίγραμμα

Περιεχόμενο μαθήματος
-
Χώροι με νόρμα, χώροι Hilbert. Παραδείγματα.
-
Ειδικές κατηγορίες τελεστών σ'ένα χώρο Hilbert.
-
Αναλλοίωτοι υπόχωροι.
-
Το φάσμα.
-
Συνεχείς συναρτήσεις ενός αυτοσυζυγούς τελεστή.
-
Το Φασματικό θεώρημα.
-
Τοπολογίες στον B(H).
-
Αβελιανές Άλγεβρες von Neumann.
Διδάσκοντες
Αριστείδης Κατάβολος
Θέση : Καθηγητής
Ερευνητικά Ενδιαφέροντα : Άλγεβρες Τελεστών, Θεωρία Τελεστών, Άλγεβρες Banach, Συναρτησιακή Ανάλυση, Αρμονική Ανάλυση
E-mail : akatavol@math.uoa.gr
Βιβλιογραφία
- W.B. Arveson, A short course in Spectral Theory, Springer-Verlag, 2002.
- A. Connes, Noncommutative Geometry, Academic Press Inc., 1994. (http://www.alainconnes.org/docs/book94bigpdf.pdf)
- J.B. Conway, A course in Functional Analysis, Springer-Verlag, 1985.
- K.R. Davidson, C∗ -Algebras by Example, Fields Institute Monographs, Amer. Math. Soc., Providence, R.I., 1996.
- R.G. Douglas, Banach Algebra Techniques in Operator Theory, Academic Press, 1972.
- J.A. Erdos, C∗ -Algebras, στο : Άλγεβρες Τελεστών και Κβαντική Μηχανική, επιμέλεια Μ. Ανούσης, Σπ. Κωτσάκης, Ν. Χατζησάββας, Εκδόσεις Ζήτη, 1997. Υπάρχει και στο http://www.mth.kcl.ac.uk/~jerdos/CS/CS.pdf.
- P.R. Halmos, Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea, N.Y., 1951.
- P.R. Halmos, A Hilbert Space Problem Book, 2nd Edition, Springer-Verlag, 1982.
- G. Helmberg, Introduction to Spectral Theory in Hilbert Space, North-Holland, 1975.
- Vaughan F. R. Jones, Lecture notes on von Neumann algebras. (https://math.berkeley.edu/~vfr/MATH20909/VonNeumann2009.pdf)
- Richard V. Kadison and John R. Ringrose, Fundamentals of the theory of operator algebras. Vol. I, volume 15 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1997. Elementary theory, Reprint of the 1983 original.
- Richard V. Kadison and John R. Ringrose, Fundamentals of the theory of operator algebras. Vol. II, volume 16 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1997. Advanced theory, Corrected reprint of the 1986 original.
- A.N. Kolmogorov & S.V. Fomin, Introductory Real Analysis, Dover 1975.
- Α. Κατάβολος, ́Αλγεβρες von Neumann και Μη Φραγμένοι Τελεστές, στο: Άλγεβρες Τελεστών και Κβαντική Μηχανική, επιμέλεια Μ. Ανούσης, Σπ. Κωτσάκης, Ν. Χατζησάββας, Εκδόσεις Ζήτη, 1997.
- Α. Κατάβολος, Εισαγωγή στη Θεωρία Τελεστών, Πανεπιστήμιο Αθηνών, 2006.
- Γ. Κουμουλλής, Σ. Νεγρεπόντης, Θεωρία Μέτρου, Εκδ. Συμμετρία, 1988.
- G.J. Murphy, C∗ -Algebras and Operator Theory, Academic Press, 1990.
- Σ. Νεγρεπόντης, Θεωρία Μιγαδικών Συναρτήσεων Μιάς Μεταβλητής, Αθήνα 1982.
- Σ. Νεγρεπόντης, Θ. Ζαχαριάδης, Ν. Καλαμίδας, Β. Φαρμάκη, Γενική Τοπολογία και Συναρτησιακή Ανάλυση, Εκδ. Συμμετρία, 1988.
- H. Radjavi & P. Rosenthal, Invariant Subspaces, Springer-Verlag, 1973. Second Edition, Dover, 2003.
- M. Reed & B. Simon, Methods of modern mathematical physics I. Functional analysis. Second edition. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York, 1980.
- W. Rudin, Functional Analysis, McGraw-Hill, 1973.
- W. Rudin, Real and Complex Analysis, McGraw-Hill, 1974.
- I.E. Segal & R.A. Kunze, Integrals and Operators, McGraw-Hill, 1968.
- V. S. Sunder, Functional analysis. Spectral theory. Birkhäuser Advanced Texts: Basel Textbooks. Birkhäuser Verlag, Basel, 1997.
- M. Takesaki, Theory of Operator Algebras I, Springer-Verlag, 1979. Second printing, Encyclopaedia of Mathematical Sciences 124, Springer, 2002.
- N.J. Young, An Introduction to Hilbert Space, Cambridge University Press, 1988.
Μαθησιακοί στόχοι
- Η μελέτη των τελεστών σε χώρους Hilbert
- Η αξιοποίηση στοιχείων της γενικής τοπολογίας και της συναρτησιακής ανάλυσης για τη μελέτη των τελεστών
- Η μελέτη του Φασματικού θεωρήματος
- Η εισαγωγή στις άλγεβρες τελεστών
Ομάδα στόχος
Μεταπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Μαθηματική Ανάλυση”.
Προαπαιτούμενα
- Πραγματική Ανάλυση
- Συναρτησιακή Ανάλυση
- Θεωρία Μέτρου
-
Χώροι με νόρμα, χώροι Hilbert. Παραδείγματα.
-
Ειδικές κατηγορίες τελεστών σ'ένα χώρο Hilbert.
-
Αναλλοίωτοι υπόχωροι.
-
Το φάσμα.
-
Συνεχείς συναρτήσεις ενός αυτοσυζυγούς τελεστή.
-
Το Φασματικό θεώρημα.
-
Τοπολογίες στον B(H).
-
Αβελιανές Άλγεβρες von Neumann.
Αριστείδης Κατάβολος
Θέση : Καθηγητής
Ερευνητικά Ενδιαφέροντα : Άλγεβρες Τελεστών, Θεωρία Τελεστών, Άλγεβρες Banach, Συναρτησιακή Ανάλυση, Αρμονική Ανάλυση
E-mail : akatavol@math.uoa.gr
- W.B. Arveson, A short course in Spectral Theory, Springer-Verlag, 2002.
- A. Connes, Noncommutative Geometry, Academic Press Inc., 1994. (http://www.alainconnes.org/docs/book94bigpdf.pdf)
- J.B. Conway, A course in Functional Analysis, Springer-Verlag, 1985.
- K.R. Davidson, C∗ -Algebras by Example, Fields Institute Monographs, Amer. Math. Soc., Providence, R.I., 1996.
- R.G. Douglas, Banach Algebra Techniques in Operator Theory, Academic Press, 1972.
- J.A. Erdos, C∗ -Algebras, στο : Άλγεβρες Τελεστών και Κβαντική Μηχανική, επιμέλεια Μ. Ανούσης, Σπ. Κωτσάκης, Ν. Χατζησάββας, Εκδόσεις Ζήτη, 1997. Υπάρχει και στο http://www.mth.kcl.ac.uk/~jerdos/CS/CS.pdf.
- P.R. Halmos, Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea, N.Y., 1951.
- P.R. Halmos, A Hilbert Space Problem Book, 2nd Edition, Springer-Verlag, 1982.
- G. Helmberg, Introduction to Spectral Theory in Hilbert Space, North-Holland, 1975.
- Vaughan F. R. Jones, Lecture notes on von Neumann algebras. (https://math.berkeley.edu/~vfr/MATH20909/VonNeumann2009.pdf)
- Richard V. Kadison and John R. Ringrose, Fundamentals of the theory of operator algebras. Vol. I, volume 15 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1997. Elementary theory, Reprint of the 1983 original.
- Richard V. Kadison and John R. Ringrose, Fundamentals of the theory of operator algebras. Vol. II, volume 16 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 1997. Advanced theory, Corrected reprint of the 1986 original.
- A.N. Kolmogorov & S.V. Fomin, Introductory Real Analysis, Dover 1975.
- Α. Κατάβολος, ́Αλγεβρες von Neumann και Μη Φραγμένοι Τελεστές, στο: Άλγεβρες Τελεστών και Κβαντική Μηχανική, επιμέλεια Μ. Ανούσης, Σπ. Κωτσάκης, Ν. Χατζησάββας, Εκδόσεις Ζήτη, 1997.
- Α. Κατάβολος, Εισαγωγή στη Θεωρία Τελεστών, Πανεπιστήμιο Αθηνών, 2006.
- Γ. Κουμουλλής, Σ. Νεγρεπόντης, Θεωρία Μέτρου, Εκδ. Συμμετρία, 1988.
- G.J. Murphy, C∗ -Algebras and Operator Theory, Academic Press, 1990.
- Σ. Νεγρεπόντης, Θεωρία Μιγαδικών Συναρτήσεων Μιάς Μεταβλητής, Αθήνα 1982.
- Σ. Νεγρεπόντης, Θ. Ζαχαριάδης, Ν. Καλαμίδας, Β. Φαρμάκη, Γενική Τοπολογία και Συναρτησιακή Ανάλυση, Εκδ. Συμμετρία, 1988.
- H. Radjavi & P. Rosenthal, Invariant Subspaces, Springer-Verlag, 1973. Second Edition, Dover, 2003.
- M. Reed & B. Simon, Methods of modern mathematical physics I. Functional analysis. Second edition. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York, 1980.
- W. Rudin, Functional Analysis, McGraw-Hill, 1973.
- W. Rudin, Real and Complex Analysis, McGraw-Hill, 1974.
- I.E. Segal & R.A. Kunze, Integrals and Operators, McGraw-Hill, 1968.
- V. S. Sunder, Functional analysis. Spectral theory. Birkhäuser Advanced Texts: Basel Textbooks. Birkhäuser Verlag, Basel, 1997.
- M. Takesaki, Theory of Operator Algebras I, Springer-Verlag, 1979. Second printing, Encyclopaedia of Mathematical Sciences 124, Springer, 2002.
- N.J. Young, An Introduction to Hilbert Space, Cambridge University Press, 1988.
- Η μελέτη των τελεστών σε χώρους Hilbert
- Η αξιοποίηση στοιχείων της γενικής τοπολογίας και της συναρτησιακής ανάλυσης για τη μελέτη των τελεστών
- Η μελέτη του Φασματικού θεωρήματος
- Η εισαγωγή στις άλγεβρες τελεστών
Μεταπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Μαθηματική Ανάλυση”.
- Πραγματική Ανάλυση
- Συναρτησιακή Ανάλυση
- Θεωρία Μέτρου
- Χώροι με νόρμα και τελεστές
- Χώροι Hilbert
- Παραδείγματα
Λέξεις κλειδιά: χώρος, νόρμα, Banach, τελεστής, φραγμένος, δυϊκός, Hilbert, εσωτερικό, γινόμενο, βάση, ορθοκανονική
- Ειδικές κατηγορίες τελεστών σ' ένα χώρο Hilbert
- Κατηγορίες τελεστών
- Αναλλοίωτοι υπόχωροι
Λέξεις κλειδιά: χώρος, Hilbert, τελεστής, sesquilinear, μορφή, τετραγωνική, ενέλιξη, φυσιολογικός, αυτοσυζυγής, θετικός, ορθομοναδιαίος, ταυτοδύναμος, ισομετρία, προβολή, υπόχωρος, αναλλοίωτος, κυκλικός
- Το Φασματικό θεώρημα σε χώρους πεπερασμένης και σε χώρους άπειρης διάστασης
Λέξεις κλειδιά: χώρος, Hilbert, τελεστής, διαγωνοποιήσιμος, θεώρημα, φασματικό
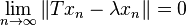
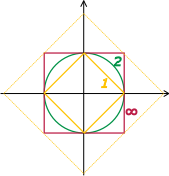
- Η έννοια του φάσματος
- Το φάσμα σε άλγεβρες Banach
- Το φάσμα ενός τελεστή
- Το φάσμα αυτοσυζυγούς τελεστή
Λέξεις κλειδιά: τελεστής, φάσμα, συνάρτηση, μετρήσιμη, άλγεβρα, Banach, ακτίνα, φασματική, σημειακό, αυτοσυζυγής
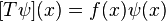
- Συνεχείς συναρτήσεις αυτοσυζυγούς τελεστή
- Ο συναρτησιακός λογισμός
- Η τετραγωνική ρίζα αυτοσυζυγούς τελεστή
- Η πολική αναπαράσταση
Λέξεις κλειδιά: τελεστής, αυτοσυζυγής, συνάρτηση, συνεχής, πολυωνυμική, μεταθέτης, αναπαράσταση, πολική
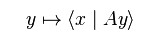
- Το Φασματικό θεώρημα για αυτοσυζυγείς τελεστές
Λέξεις κλειδιά: τελεστής, αυτοσυζυγής, φραγμένος, διάνυσμα, κυκλικό, θεώρημα, φασματικό, άθροισμα, ευθύ
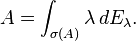
- Το Φασματικό θεώρημα : δεύτερη μορφή
- Ολοκλήρωση ως προς φασματικό μέτρο
- Μέτρα και αναπαραστάσεις
- Το φασματικό θεώρημα
- Επέκταση του συναρτησιακού λογισμού
Λέξεις κλειδιά: θεώρημα, φασματικό, τελεστής, χώρος, Hilbert, μέτρο, ολοκλήρωση, κανονικό, αναπαράσταση, μεταθέτης, άλγεβρα, von Neumann, φυσιολογικός, αυτοσυζυγής, ακτίνα, αριθμητική
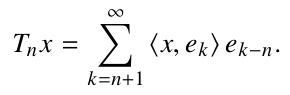
- Τοπολογίες στον Β(Η)
- Η ισχυρή τοπολογία τελεστών (SOT)
- Η ασθενής τοπολογία τελεστών (WOT)
- Ο Β(Η) ως δυϊκός χώρος Banach
- Η ασθενής *-τοπολογία
Λέξεις κλειδιά: χώρος, Β(Η), Hilbert, τοπολογία, τελεστές, ισχυρή, ασθενής, θήκη, γραμμική, ανακλαστική, δυϊκός, Banach, υπερασθενής, προδυϊκός

- Αβελιανές άλγεβρες von Neumann
- Κάθε masa είναι πολλαπλασιαστική άλγεβρα
Λέξεις κλειδιά: άλγεβρα, αβελιανή, von Neumann, χώρος, Hilbert, τελεστής, μεταθέτης, πολλαπλασιαστική, ισοδύναμα, ορθομοναδιαία, μεγιστική, διάνυσμα, διαχωρίζον, κυκλικό, μέτρο, θεώρημα, φασματικό
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -