Αρμονική Ανάλυση
Απόστολος Γιαννόπουλος
To μεταπτυχιακό μάθημα “Αρμονική Ανάλυση” προσφέρεται ως μάθημα επιλογής στο μεταπτυχιακό πρόγραμμα “Θεωρητικά Μαθηματικά”.
Στις πρώτες τρεις ενότητες του μαθήματος παρουσιάζονται οι έννοιες του μέτρου και του ολοκληρώματος Lebesgue, καθώς και μία σύγκριση μεταξύ του ολοκληρώματος Riemann με το ολοκλήρωμα Lebesgue.
Στην τέταρτη ενότητα παρουσιάζονται οι χώροι Lp, τα θεωρήματα Riesz-Fischer και Fubini, καθώς και η έννοια της συνέλιξης.
Στην πέμπτη ενότητα μελετώνται οι σειρές Fourier ολοκληρώσιμων και συνεχών συναρτήσεων και τα τριγωνομετρικά πολυώνυμα ενώ παρουσιάζονται ακόμη ο πυρήνας του Dirichlet και τα θεωρήματα των Dini και Marcinkiewicz.
Στην έκτη ενότητα παρουσιάζονται οι έννοιες της οικογένειας καλών πυρήνων και των προσεγγίσεων της μονάδας και μελετώνται η αθροισιμότητα κατά Cesàro και κατά Abel καθώς και οι πυρήνες Fejér και Poisson.
Στην έβδομη ενότητα είσαγεται η έννοια του χώρου Hilbert και μελετάται η L2-σύγκλιση σειρών Fourier στο χώρο L2(T).
Στην όγδοη ενότητα παρουσιάζεται ο μετασχηματισμός Fourier.
Στην ένατη και στη δέκατη ενότητα μελετώνται η Lp-σύγκλιση και ο μετασχηματισμός Hilbert στο χώρο Lp(T), αντίστοιχα.
Τέλος, στην ενδέκατη ενότητα παρουσιάζεται το θεώρημα παρεμβολής του Riesz καθώς και η ανισότητα των Hausdorff-Young.
Λιγότερα
To μεταπτυχιακό μάθημα “Αρμονική Ανάλυση” προσφέρεται ως μάθημα επιλογής στο μεταπτυχιακό πρόγραμμα “Θεωρητικά Μαθηματικά”.
Στις πρώτες τρεις ενότητες του μαθήματος παρουσιάζονται οι έννοιες του μέτρου και του ολοκληρώματος Lebesgue, καθώς και μία σύγκριση μεταξύ του ολοκληρώματος Riemann με το ολοκλήρωμα Lebesgue.
Στην τέταρτη ενότητα παρουσιάζονται οι χώροι Lp, τα θεωρήματα Riesz-Fischer και Fubini, καθώς και η έννοια της συνέλιξης.
Στην πέμπτη ενότητα μελετώνται οι σειρές Fourier ολοκληρώσιμων και συνεχών συναρτήσεων και τα τριγωνομετρικά πολυώνυμα ενώ παρουσιάζονται ακόμη ο πυρήνας του Dirichlet και τα θεωρήματα των Dini και Marcinkiewicz.
Στην έκτη ενότητα παρουσιάζονται οι έννοιες της οικογένειας καλών πυρήνων και των προσεγγίσεων της μονάδας και μελετώνται η αθροισιμότητα κατά Cesàro και κατά Abel καθώς και οι πυρήνες Fejér και Poisson.
Στην έβδομη ενότητα είσαγεται η έννοια του χώρου Hilbert και μελετάται η L2-σύγκλιση σειρών Fourier στο χώρο L2(T).
Στην όγδοη ενότητα παρουσιά
To μεταπτυχιακό μάθημα “Αρμονική Ανάλυση” προσφέρεται ως μάθημα επιλογής στο μεταπτυχιακό πρόγραμμα “Θεωρητικά Μαθηματικά”.
Στις πρώτες τρεις ενότητες του μαθήματος παρουσιάζονται οι έννοιες του μέτρου και του ολοκληρώματος Lebesgue, καθώς και μία σύγκριση μεταξύ του ολοκληρώματος Riemann με το ολοκλήρωμα Lebesgue.
Στην τέταρτη ενότητα παρουσιάζονται οι χώροι Lp, τα θεωρήματα Riesz-Fischer και Fubini, καθώς και η έννοια της συνέλιξης.
Στην πέμπτη ενότητα μελετώνται οι σειρές Fourier ολοκληρώσιμων και συνεχών συναρτήσεων και τα τριγωνομετρικά πολυώνυμα ενώ παρουσιάζονται ακόμη ο πυρήνας του Dirichlet και τα θεωρήματα των Dini και Marcinkiewicz.
Στην έκτη ενότητα παρουσιάζονται οι έννοιες της οικογένειας καλών πυρήνων και των προσεγγίσεων της μονάδας και μελετώνται η αθροισιμότητα κατά Cesàro και κατά Abel καθώς και οι πυρήνες Fejér και Poisson.
Στην έβδομη ενότητα είσαγεται η έννοια του χώρου Hilbert και μελετάται η L2-σύγκλιση σειρών Fourier στο χώρο L2(T).
Στην όγδοη ενότητα παρουσιά
Περίγραμμα

Διδάσκοντες
Απόστολος Γιαννόπουλος
Θέση : Καθηγητής
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
Περιεχόμενο μαθήματος
- Μέτρο Lebesgue
- Ολοκλήρωμα Lebesgue
- Ολοκλήρωμα Riemann και ολοκλήρωμα Lebesgue
- Χώροι Lp
- Σειρές Fourier
- Προσεγγίσεις της μονάδας και αθροισιμότητα
- L2 σύγκλιση σειρών Fourier
- Μετασχηματισμός Fourier
- Lp-σύγκλιση
- Ο μετασχηματισμός Hilbert στον Lp(T)
- Το θεώρημα παρεμβολής του Riesz και η ανισότητα Hausdorff-Young
Βιβλιογραφία
- Helson, Henry . Harmonic analysis. Second edition. Texts and Readings in Mathematics, 7. Hindustan Book Agency, New Delhi, 2010.
- Folland, Gerald B. Real analysis. Modern techniques and their applications. Second edition. Pure and Applied Mathematics, John Wiley & Sons, Inc., New York, 1999.
- Katznelson, Yitzhak. An introduction to harmonic analysis. 3rd edition. Cambridge University Press, 2004.
- Rudin, Walter. Functional analysis. 2nd edition. McGraw-Hill, 1991.
- Rudin, W. Real and complex analysis. 3rd edition. McGraw-Hill, 1987.
- Stein, Elias M. ; Shakarchi, Rami . Fourier analysis. An introduction. Princeton Lectures in Analysis, 1. Princeton University Press, Princeton, NJ, 2003.
- Dym, H. ; McKean, H. P. Fourier series and integrals. Probability and Mathematical Statistics, No. 14. Academic Press, New York-London, 1972.
Μαθησιακοί στόχοι
- Η μελέτη βασικών εννοιών της θεωρίας Μέτρου για τη διαδικασία ολοκλήρωσης κατά Lebesgue
- Η μέλετη των σειρών Fourier και της σύγκλισης των σειρών Fourier
- Η παρουσίαση στοιχείων της Συναρτησιακής Ανάλυσης που βοηθούν στη μελέτη των σειρών Fourier
Ομάδα στόχος
Μεταπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Μαθηματική Ανάλυση”.
Προαπαιτούμενα
- Πραγματική Ανάλυση
- Στοιχειώδης Θεωρία Μέτρου
Απόστολος Γιαννόπουλος
Θέση : Καθηγητής
Ερευνητικά Ενδιαφέροντα : Κυρτή Γεωμετρική Ανάλυση, Συναρτησιακή Ανάλυση, Πιθανοθεωρητικές Μέθοδοι
E-mail : apgiannop@math.uoa.gr
- Μέτρο Lebesgue
- Ολοκλήρωμα Lebesgue
- Ολοκλήρωμα Riemann και ολοκλήρωμα Lebesgue
- Χώροι Lp
- Σειρές Fourier
- Προσεγγίσεις της μονάδας και αθροισιμότητα
- L2 σύγκλιση σειρών Fourier
- Μετασχηματισμός Fourier
- Lp-σύγκλιση
- Ο μετασχηματισμός Hilbert στον Lp(T)
- Το θεώρημα παρεμβολής του Riesz και η ανισότητα Hausdorff-Young
- Helson, Henry . Harmonic analysis. Second edition. Texts and Readings in Mathematics, 7. Hindustan Book Agency, New Delhi, 2010.
- Folland, Gerald B. Real analysis. Modern techniques and their applications. Second edition. Pure and Applied Mathematics, John Wiley & Sons, Inc., New York, 1999.
- Katznelson, Yitzhak. An introduction to harmonic analysis. 3rd edition. Cambridge University Press, 2004.
- Rudin, Walter. Functional analysis. 2nd edition. McGraw-Hill, 1991.
- Rudin, W. Real and complex analysis. 3rd edition. McGraw-Hill, 1987.
- Stein, Elias M. ; Shakarchi, Rami . Fourier analysis. An introduction. Princeton Lectures in Analysis, 1. Princeton University Press, Princeton, NJ, 2003.
- Dym, H. ; McKean, H. P. Fourier series and integrals. Probability and Mathematical Statistics, No. 14. Academic Press, New York-London, 1972.
- Η μελέτη βασικών εννοιών της θεωρίας Μέτρου για τη διαδικασία ολοκλήρωσης κατά Lebesgue
- Η μέλετη των σειρών Fourier και της σύγκλισης των σειρών Fourier
- Η παρουσίαση στοιχείων της Συναρτησιακής Ανάλυσης που βοηθούν στη μελέτη των σειρών Fourier
Μεταπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Μαθηματική Ανάλυση”.
- Πραγματική Ανάλυση
- Στοιχειώδης Θεωρία Μέτρου
- Εξωτερικό μέτρο Lebesgue
- Lebesgue μετρήσιμα σύνολα
- Mέτρο Lebesgue
Λέξεις κλειδιά: μέτρο, εξωτερικό, Lebesgue, μετρήσιμο, σύνολο, Borel, Cantor, Vitali, λήμμα Steinhaus
- Μετρήσιμες συναρτήσεις
- Oλοκλήρωμα Lebesgue
Λέξεις κλειδιά: συνάρτηση, μετρήσιμη, απλή, Cantor, Lebesgue, Littlewood, ολοκλήρωμα, σύγκλιση, κυριαρχημένη
- Σύγκριση του ολοκληρώματος Lebesgue με το ολοκλήρωμα Riemann
- Το θεώρημα παραγώγισης του Lebesgue
- Συναρτήσεις φραγμένης κύμανσης
- Παραγωγισιμότητα μονότονων συναρτήσεων
- Απόλυτα συνεχείς συναρτήσεις
Λέξεις κλειδιά: ολοκλήρωμα, Lebesgue, Riemann, παραγώγιση, κύμανση, φραγμένη, συνάρτηση, μονότονη, απόλυτα συνεχής
- Χώροι Lp
- Θεώρημα Riesz-Fischer
- Θεώρημα Fubini
- Συνέλιξη
Λέξεις κλειδιά: χώρος, Lp, Riesz, Fischer, Fubini, θεώρημα, συνέλιξη
- Σειρές Fourier ολοκληρώσιμων συναρτήσεων
- Τριγωνομετρικά πολυώνυμα
- Βασικές ιδιότητες των σειρών Fourier
- Ο πυρήνας του Dirichlet
- Σειρές Fourier συνεχών συναρτήσεων
- Θεώρημα Dini και θεώρημα Marcinkiewicz
Λέξεις κλειδιά: σειρά, Fourier, συνάρτηση, ολοκληρώσιμη, συνεχής, πολυώνυμο, τριγωνομετρικό, πυρήνας, Dirichlet, θεώρημα, Dini, Marcinkiewicz
- Οικογένειες καλών πυρήνων και προσεγγίσεων της μονάδας
- Cesàro αθροισιμότητα
- Ο πυρήνας του Fejér
- Χαρακτηρισμός των τριγωνομετρικών σειρών που είναι σειρές Fourier
- Abel αθροισιμότητα και ο πυρήνας του Poisson
Λέξεις κλειδιά: πυρήνας, μονάδα, προσεγγίσεις, αθροισιμότητα, Cesàro, Fejér, σειρά, τριγωνομετρική, Fourier, Abel, Poisson
- Χώροι Hilbert
- Σύγκλιση στον L2(T)
Λέξεις κλειδιά: χώρος, Hilbert, εσωτερικό, γινόμενο, καθετότητα, βάση, ορθοκανονική, σύγκλιση
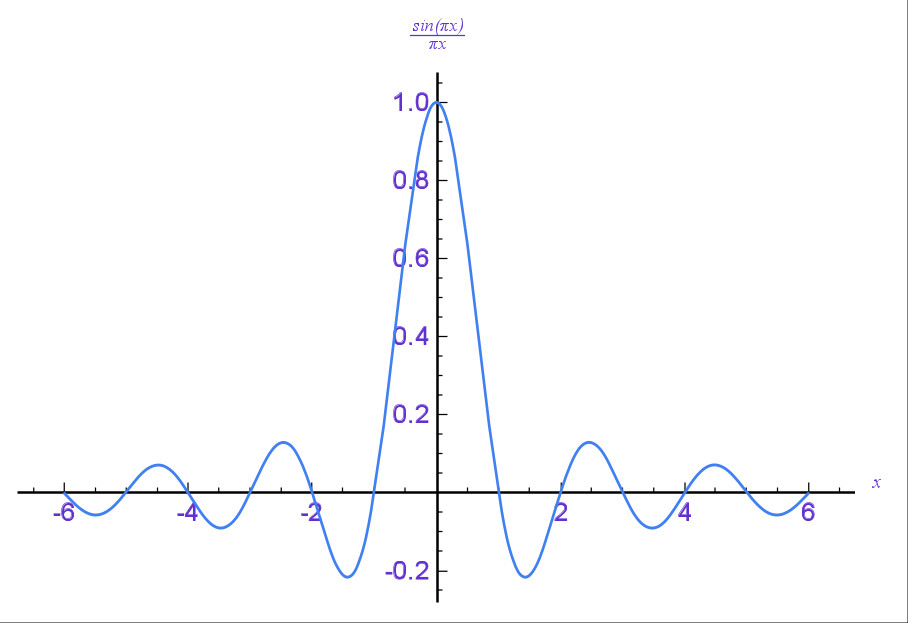
- Μετασχηματισμός Fourier
Λέξεις κλειδιά: μετασχηματισμός, Fourier, τύπος, αντιστροφής
- Lp-σύγκλιση
Λέξεις κλειδιά: σύγκλιση, Lp, αναπαράσταση, απεικόνιση, συζυγής
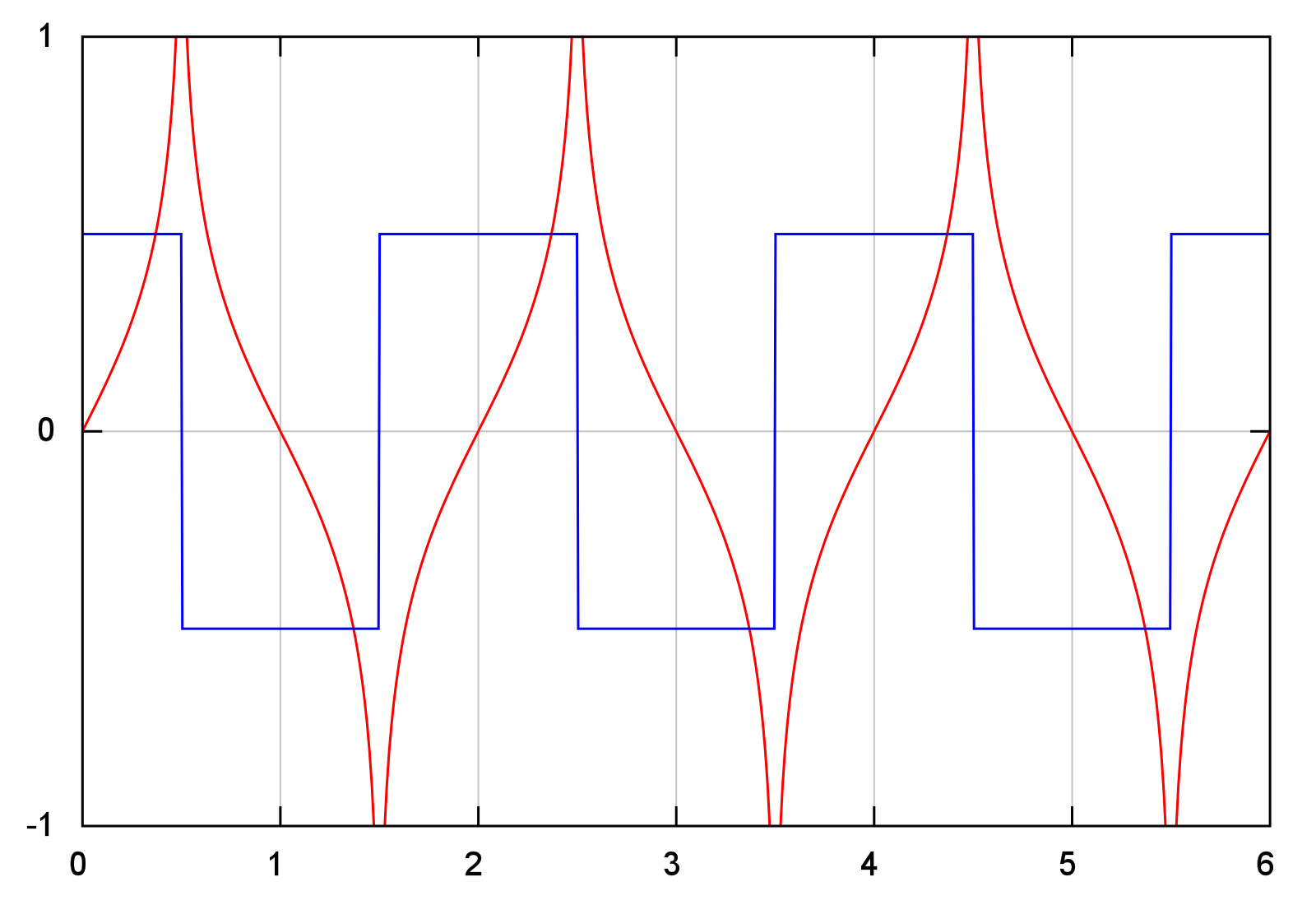
- Ο μετασχηματισμός Hilbert στον Lp(T)
Λέξεις κλειδιά: θεώρημα, παρεμβολή, Marcinkiewicz, διάσπαση, Calderón, Zygmund, μετασχηματισμός, Hilbert, κλάση
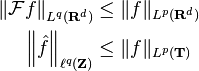
- Το θεώρημα παρεμβολής του Riesz
- Η ανισότητα Hausdorff-Young
Λέξεις κλειδιά: θεώρημα, παρεμβολή, Riesz, ανισότητα, Hausdorff, Young
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -