Γραμμική Άλγεβρα Ι
Ευάγγελος Ράπτης
Η Γραμμική Άλγεβρα, εκτός από τη σημαντική της συνεισφορά στην ανάπτυξη άλλων κλάδων των Μαθηματικών, βρίσκει εφαρμογές στη Φυσική, τη Μηχανική, τη Βιολογία και την Οικονομία.
Μία βασική έννοια για τη μελέτη των γραμμικών συναρτήσεων είναι αυτή του διανυσματικού χώρου, ενώ ένα πολύ χρήσιμο εργαλείο για την κατανόησή τους είναι ο λογισμός των πινάκων.
Στην πρώτη ενότητα του μαθήματος παρουσιάζονται ορισμένες απαραίτητες εισαγωγικές έννοιες, καθώς και η σχέση των συστημάτων γραμμικών εξισώσεων με τους πίνακες.
Στη δεύτερη ενότητα εισάγονται και μελετώνται οι διανυσματικοί χώροι και οι υπόχωροι τους. Περιγράφεται η σχέση της γραμμικής εξάρτησης και δίνεται ένας αποτελεσματικός τρόπος για την περιγραφή των χώρων αυτών, μέσω της έννοιας της βάσης. Ορίζεται επίσης η διάσταση ενός διανυσματικού χώρου, η οποία αποτελεί βασικό εργαλείο για την ανάπτυξη της θεωρίας.
Στην τρίτη ενότητα εισάγεται η έννοια των γραμμικών απεικονίσεων μεταξύ δυο διανυσματικών χώρων και εξετάζονται διάφορες ιδιότητές τους. Μεταξύ άλλων, αποδεικνύεται ότι δύο διανυσματικοί χώροι είναι ισόμορφοι αν και μόνο αν έχουν την ίδια διάσταση. Επίσης, εξετάζεται ο τρόπος με τον οποίο μπορούμε να πάρουμε πληροφορίες για μία γραμμική απεικόνιση μελετώντας τον πυρήνα και την εικόνα της.
Τέλος, στην τέταρτη ενότητα εισάγεται η έννοια της ορίζουσας ενός τετραγωνικού πίνακα και συνδέεται η αφηρημένη έννοια της γραμμικής απεικόνισης με τη θεωρία των πινάκων. Χρησιμοποιώντας τον αλγεβρικό λογισμό των πινάκων, η σχέση αυτή οδηγεί σε μία καλύτερη κατανόηση των γραμμικών απεικονίσεων, καθώς επίσης και σε μία περαιτέρω εμβάθυνση στη μελέτη του συνόλου των λύσεων συστημάτων γραμμικών εξισώσεων.
Λιγότερα
Η Γραμμική Άλγεβρα, εκτός από τη σημαντική της συνεισφορά στην ανάπτυξη άλλων κλάδων των Μαθηματικών, βρίσκει εφαρμογές στη Φυσική, τη Μηχανική, τη Βιολογία και την Οικονομία.
Μία βασική έννοια για τη μελέτη των γραμμικών συναρτήσεων είναι αυτή του διανυσματικού χώρου, ενώ ένα πολύ χρήσιμο εργαλείο για την κατανόησή τους είναι ο λογισμός των πινάκων.
Στην πρώτη ενότητα του μαθήματος παρουσιάζονται ορισμένες απαραίτητες εισαγωγικές έννοιες, καθώς και η σχέση των συστημάτων γραμμικών εξισώσεων με τους πίνακες.
Στη δεύτερη ενότητα εισάγονται και μελετώνται οι διανυσματικοί χώροι και οι υπόχωροι τους. Περιγράφεται η σχέση της γραμμικής εξάρτησης και δίνεται ένας αποτελεσματικός τρόπος για την περιγραφή των χώρων αυτών, μέσω της έννοιας της βάσης. Ορίζεται επίσης η διάσταση ενός διανυσματικού χώρου, η οποία αποτελεί βασικό εργαλείο για την ανάπτυξη της θεωρίας.
Στην τρίτη ενότητα εισάγεται η έννοια των γραμμικών απεικονίσεων μεταξύ δυο διανυσματικών χώρων και εξετάζονται διάφορες ιδιότητές
Η Γραμμική Άλγεβρα, εκτός από τη σημαντική της συνεισφορά στην ανάπτυξη άλλων κλάδων των Μαθηματικών, βρίσκει εφαρμογές στη Φυσική, τη Μηχανική, τη Βιολογία και την Οικονομία.
Μία βασική έννοια για τη μελέτη των γραμμικών συναρτήσεων είναι αυτή του διανυσματικού χώρου, ενώ ένα πολύ χρήσιμο εργαλείο για την κατανόησή τους είναι ο λογισμός των πινάκων.
Στην πρώτη ενότητα του μαθήματος παρουσιάζονται ορισμένες απαραίτητες εισαγωγικές έννοιες, καθώς και η σχέση των συστημάτων γραμμικών εξισώσεων με τους πίνακες.
Στη δεύτερη ενότητα εισάγονται και μελετώνται οι διανυσματικοί χώροι και οι υπόχωροι τους. Περιγράφεται η σχέση της γραμμικής εξάρτησης και δίνεται ένας αποτελεσματικός τρόπος για την περιγραφή των χώρων αυτών, μέσω της έννοιας της βάσης. Ορίζεται επίσης η διάσταση ενός διανυσματικού χώρου, η οποία αποτελεί βασικό εργαλείο για την ανάπτυξη της θεωρίας.
Στην τρίτη ενότητα εισάγεται η έννοια των γραμμικών απεικονίσεων μεταξύ δυο διανυσματικών χώρων και εξετάζονται διάφορες ιδιότητές
Περίγραμμα

Διδάσκοντες
Ευάγγελος Ράπτης
Θέση: Καθηγητής, Τμήμα Μαθηματικών
Ερευνητικά ενδιαφέροντα: Θεωρία ομάδων
Περιεχόμενο μαθήματος
- Πίνακες και γραμμικά συστήματα
- Διανυσματικοί χώροι
- Γραμμικές απεικονίσεις
- Πίνακες και γραμμικές απεικονίσεις
- Ορίζουσες
- Γραμμικά συστήματα
Μαθησιακοί στόχοι
- Επίλυση γραμμικών συστημάτων με χρήση πινάκων
- Εξοικείωση με τις έννοιες του διανυσματικού χώρου, του υποχώρου, της βάσης και της διάστασης ενός υποχώρου
- Εξοικείωση με τις έννοιες της γραμμικής απεικόνισης, του πυρήνα και της εικόνας μίας γραμμικής απεικόνισης και του ισομορφισμού
- Σύνδεση της έννοιας της γραμμικής απεικόνισης με τη θεωρία των πινάκων
- Μελέτη του συνόλου λύσεων συστημάτων γραμμικών εξισώσεων
Προτεινόμενα συγγράμματα
Δ. Βάρσος, Δ. Δεριζιώτης, Μ. Μαλιάκας, Στ. Παπασταυρίδης, Ε. Ράπτης, Ο. Ταλέλλη: “Εισαγωγή στη Γραμμική Άλγεβρα” Τόμος Α.
Ευάγγελος Ράπτης
Θέση: Καθηγητής, Τμήμα Μαθηματικών
Ερευνητικά ενδιαφέροντα: Θεωρία ομάδων
- Πίνακες και γραμμικά συστήματα
- Διανυσματικοί χώροι
- Γραμμικές απεικονίσεις
- Πίνακες και γραμμικές απεικονίσεις
- Ορίζουσες
- Γραμμικά συστήματα
- Επίλυση γραμμικών συστημάτων με χρήση πινάκων
- Εξοικείωση με τις έννοιες του διανυσματικού χώρου, του υποχώρου, της βάσης και της διάστασης ενός υποχώρου
- Εξοικείωση με τις έννοιες της γραμμικής απεικόνισης, του πυρήνα και της εικόνας μίας γραμμικής απεικόνισης και του ισομορφισμού
- Σύνδεση της έννοιας της γραμμικής απεικόνισης με τη θεωρία των πινάκων
- Μελέτη του συνόλου λύσεων συστημάτων γραμμικών εξισώσεων
Δ. Βάρσος, Δ. Δεριζιώτης, Μ. Μαλιάκας, Στ. Παπασταυρίδης, Ε. Ράπτης, Ο. Ταλέλλη: “Εισαγωγή στη Γραμμική Άλγεβρα” Τόμος Α.

- Στοιχεία θεωρίας συνόλων
- Γραμμικά συστήματα
- Εσωτερικά γινόμενα
- Πίνακες
- Σχέσεις ισοδυναμίας
- Πίνακες και γραμμικά συστήματα
Λέξεις κλειδιά: σύνολο, γραμμικό σύστημα, εσωτερικό γινόμενο, πίνακας, σχέση ισοδυναμίας
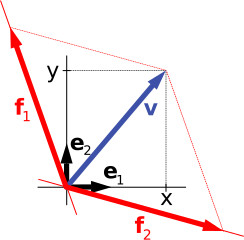
- Η έννοια του διανυσματικού χώρου
- Η έννοια του υπόχωρου
- Τομή υπόχωρων
- Γεννήτορες υπόχωρου - γραμμική θήκη υπόχωρων
- Βάση διανυσματικού χώρου
- Γραμμική ανεξαρτησία
- Διάσταση διανυσματικού χώρου
- Θεώρημα ανταλλαγής, θεώρημα επέκτασης
Λέξεις κλειδιά: διανυσματικός χώρος, υπόχωρος, γεννήτορες, γραμμική θήκη, βάση, διάσταση, γραμμική ανεξαρτησία
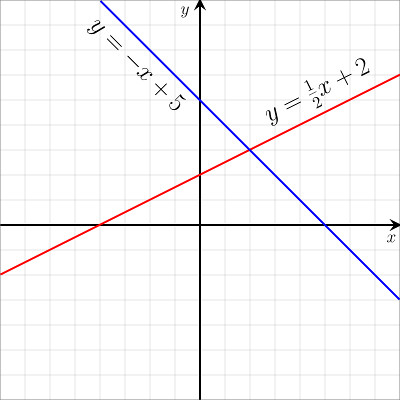
- Η έννοια της γραμμικής απεικόνισης
- Πυρήνας και εικόνα γραμμικής απεικόνισης
- Πίνακας γραμμικής απεικόνισης
- Ισομορφισμοί διανυσματικών χώρων
- Γραμμικές απεικονίσεις και πίνακες
- Απλή μορφή πίνακα γραμμικής απεικόνισης
- Τάξη πίνακα
Λέξεις κλειδιά: γραμμική απεικόνιση, πυρήνας, εικόνα, πίνακας, ισομορφισμός, απλή μορφή, τάξη πίνακα
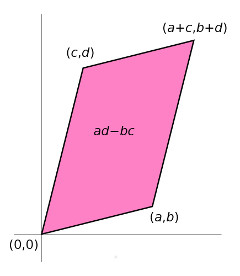
- Η έννοια της ορίζουσας ενός τετραγωνικού πίνακα
- Η ορίζουσα ενός πίνακα 3x3
- Μεταθέσεις στοιχείων
- Ορίζουσα γινομένου δύο τετραγωνικών πινάκων
- Ανάπτυγμα ορίζουσας
- Ορίζουσα και αντιστρεψιμότητα πίνακα
- Τετραγωνικά γραμμικά συστήματα
- Επίλυση ομογενούς γραμμικού συστήματος
- Μη ομογενή γραμμικά συστήματα
- Σύμπλοκα υποχώρων
- Ο χώρος πηλίκο
Λέξεις κλειδιά: ορίζουσα, μεταθέσεις, ανάπτυγμα, πίνακας, αντιστρέψιμος, αντίστροφος, γραμμικό σύστημα, ομογενές, σύμπλοκα, χώρος πηλίκο
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -