Διδασκαλία των Μαθηματικών με Διαδικασίες Επίλυσης Προβλημάτων
Νικόλαος Κλαουδάτος
Το μάθημα αυτό αποτελεί την πρακτική άσκηση των φοιτητών. Για το λόγο αυτό βασικό στοιχείο του μαθήματος, εκτός από τα μαθήματα στην αίθουσα διδασκαλίας, είναι η ανάπτυξη διδακτικών ενοτήτων από ομάδες φοιτητών, οι οποίες κατόπιν διδάσκονται από τους ίδιους σε μαθητές επιλεγμένων σχολείων.
- Η έννοια του προβλήματος και η κεντρική θέση του τόσο στην εξέλιξη των μαθηματικών εννοιών όσο και στη διδασκαλία τους.
- Ιστορική επισκόπηση: Ο Αρχιμήδης και η μηχανική μέθοδος. Η ανάδυση των πρώτων ευρετικών (στρατηγικών). Ο ρόλος του Γαλιλαίου στην ανάπτυξη της πειραματικής επιστήμης, η ‘Μέθοδος’ του Καρτέσιου. Ιδέες και παραδείγματα στη λύση προβλήματος από τον Euler.
- Η νεώτερη ιστορία της λύσης μαθηματικού προβλήματος( mathematical problem solving). Οι ιδέες του Polya, η ́Μέθοδος’, η έννοια της ευρετικής (heuristic), πρόσφατα ερευνητικά συμπεράσματα για τη μέθοδο του Polya. Οι σύγχρονες αντιλήψεις για την έννοια της ευρετικής.
- Λύση πραγματικού προβλήματος (applied problem solving): Η μοντελοποίηση (mathematical modeling), οι βασικές ιδέες και έννοιες.
- Σύγκριση της επίλυσης μαθηματικού και πραγματικού προβλήματος. Ομοιότητες και διαφορές. Τα Μαθηματικά ως δίκτυο αλληλοσυνδεόμενων προβλημάτων: Η ενοποιημένη αντίληψη για τη λύση προβλήματος.
- Ο ρόλος του Η/Υ στη λύση προβλήματος.
Το μάθημα αυτό αποτελεί την πρακτική άσκηση των φοιτητών. Για το λόγο αυτό βασικό στοιχείο του μαθήματος, εκτός από τα μαθήματα στην αίθουσα διδασκαλίας, είναι η ανάπτυξη διδακτικών ενοτήτων από ομάδες φοιτητών, οι οποίες κατόπιν διδάσκονται από τους ίδιους σε μαθητές επιλεγμένων σχολείων.
- Η έννοια του προβλήματος και η κεντρική θέση του τόσο στην εξέλιξη των μαθηματικών εννοιών όσο και στη διδασκαλία τους.
- Ιστορική επισκόπηση: Ο Αρχιμήδης και η μηχανική μέθοδος. Η ανάδυση των πρώτων ευρετικών (στρατηγικών). Ο ρόλος του Γαλιλαίου στην ανάπτυξη της πειραματικής επιστήμης, η ‘Μέθοδος’ του Καρτέσιου. Ιδέες και παραδείγματα στη λύση προβλήματος από τον Euler.
- Η νεώτερη ιστορία της λύσης μαθηματικού προβλήματος( mathematical problem solving). Οι ιδέες του Polya, η ́Μέθοδος’, η έννοια της ευρετικής (heuristic), πρόσφατα ερευνητικά συμπεράσματα για τη μέθοδο του Polya. Οι σύγχρονες αντιλήψεις για την έννοια της ευρετικής.
- Λύση πραγματικού προβλήματος (applied problem solving): Η μοντελοποίηση
Το μάθημα αυτό αποτελεί την πρακτική άσκηση των φοιτητών. Για το λόγο αυτό βασικό στοιχείο του μαθήματος, εκτός από τα μαθήματα στην αίθουσα διδασκαλίας, είναι η ανάπτυξη διδακτικών ενοτήτων από ομάδες φοιτητών, οι οποίες κατόπιν διδάσκονται από τους ίδιους σε μαθητές επιλεγμένων σχολείων.
- Η έννοια του προβλήματος και η κεντρική θέση του τόσο στην εξέλιξη των μαθηματικών εννοιών όσο και στη διδασκαλία τους.
- Ιστορική επισκόπηση: Ο Αρχιμήδης και η μηχανική μέθοδος. Η ανάδυση των πρώτων ευρετικών (στρατηγικών). Ο ρόλος του Γαλιλαίου στην ανάπτυξη της πειραματικής επιστήμης, η ‘Μέθοδος’ του Καρτέσιου. Ιδέες και παραδείγματα στη λύση προβλήματος από τον Euler.
- Η νεώτερη ιστορία της λύσης μαθηματικού προβλήματος( mathematical problem solving). Οι ιδέες του Polya, η ́Μέθοδος’, η έννοια της ευρετικής (heuristic), πρόσφατα ερευνητικά συμπεράσματα για τη μέθοδο του Polya. Οι σύγχρονες αντιλήψεις για την έννοια της ευρετικής.
- Λύση πραγματικού προβλήματος (applied problem solving): Η μοντελοποίηση
Περίγραμμα

Περιεχόμενο μαθήματος
- Η έννοια του προβλήματος και η κεντρική θέση του τόσο στην εξέλιξη των μαθηματικών εννοιών όσο και στη διδασκαλία τους.
- Ιστορική επισκόπηση: Ο Αρχιμήδης και η μηχανική μέθοδος. Η ανάδυση των πρώτων ευρετικών (στρατηγικών). Ο ρόλος του Γαλιλαίου στην ανάπτυξη της πειραματικής επιστήμης, η ‘Μέθοδος’ του Καρτέσιου. Ιδέες και παραδείγματα στη λύση προβλήματος από τον Euler.
- Η νεώτερη ιστορία της λύσης μαθηματικού προβλήματος( mathematical problem solving). Οι ιδέες του Polya, η ́Μέθοδος’, η έννοια της ευρετικής (heuristic), πρόσφατα ερευνητικά συμπεράσματα για τη μέθοδο του Polya. Οι σύγχρονες αντιλήψεις για την έννοια της ευρετικής.
- Λύση πραγματικού προβλήματος (applied problem solving): Η μοντελοποίηση (mathematical modeling), οι βασικές ιδέες και έννοιες.
- Σύγκριση της επίλυσης μαθηματικού και πραγματικού προβλήματος. Ομοιότητες και διαφορές. Τα Μαθηματικά ως δίκτυο αλληλοσυνδεόμενων προβλημάτων: Η ενοποιημένη αντίληψη για τη λύση προβλήματος.
- Ο ρόλος του Η/Υ στη λύση προβλήματος.
Διδάσκοντες
Νικόλαος Κλαουδάτος
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
- Η έννοια του προβλήματος και η κεντρική θέση του τόσο στην εξέλιξη των μαθηματικών εννοιών όσο και στη διδασκαλία τους.
- Ιστορική επισκόπηση: Ο Αρχιμήδης και η μηχανική μέθοδος. Η ανάδυση των πρώτων ευρετικών (στρατηγικών). Ο ρόλος του Γαλιλαίου στην ανάπτυξη της πειραματικής επιστήμης, η ‘Μέθοδος’ του Καρτέσιου. Ιδέες και παραδείγματα στη λύση προβλήματος από τον Euler.
- Η νεώτερη ιστορία της λύσης μαθηματικού προβλήματος( mathematical problem solving). Οι ιδέες του Polya, η ́Μέθοδος’, η έννοια της ευρετικής (heuristic), πρόσφατα ερευνητικά συμπεράσματα για τη μέθοδο του Polya. Οι σύγχρονες αντιλήψεις για την έννοια της ευρετικής.
- Λύση πραγματικού προβλήματος (applied problem solving): Η μοντελοποίηση (mathematical modeling), οι βασικές ιδέες και έννοιες.
- Σύγκριση της επίλυσης μαθηματικού και πραγματικού προβλήματος. Ομοιότητες και διαφορές. Τα Μαθηματικά ως δίκτυο αλληλοσυνδεόμενων προβλημάτων: Η ενοποιημένη αντίληψη για τη λύση προβλήματος.
- Ο ρόλος του Η/Υ στη λύση προβλήματος.
Νικόλαος Κλαουδάτος
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
 Οριοθέτηση της έννοιας
Οριοθέτηση της έννοιας- Οι ιδέες του G. Polya (1973 a, 1973 b, 1965)
- Η μέθοδος
- Η έννοια της Ευρετικής
- Η ανάπτυξη ιδεών του Polya
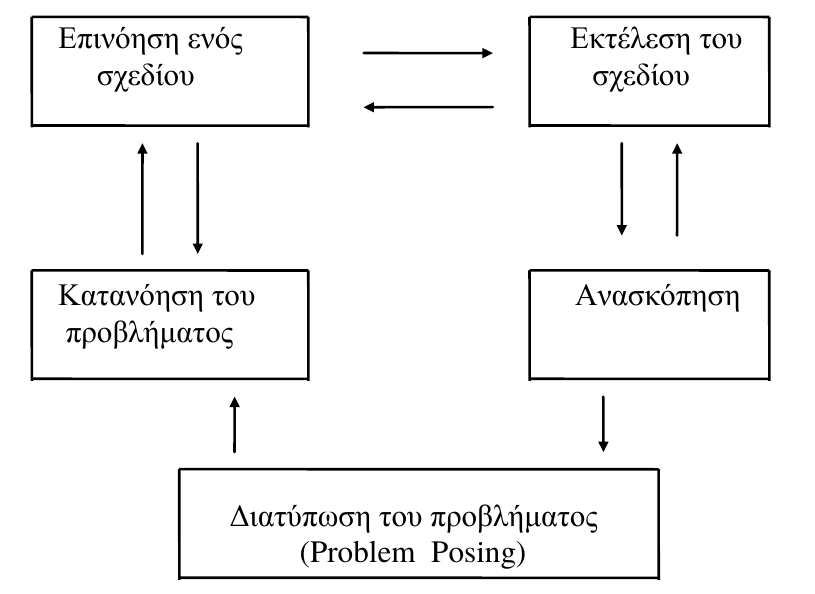
- Κατανόηση του προβλήματος (Ανάλυση)
- Ανάπτυξη ενός σχεδίου (Διερεύνηση)
- Εκτέλεση ενός σχεδίου (Επαλήθευση)
- Ανασκόπηση (Επαλήθευση)
- Λύση του Μαθηματικού Προβλήματος
- Λύση του Μαθηματικού Προβλήματος ως Διαδικασία
- Βασικές Συνιστώσες της λύσης του προβλήματος
- Σχεδίαση Διδασκαλίας
- Γενικότερες Ιδέες για την Λύση Προβλήματος και στην Διδασκαλία
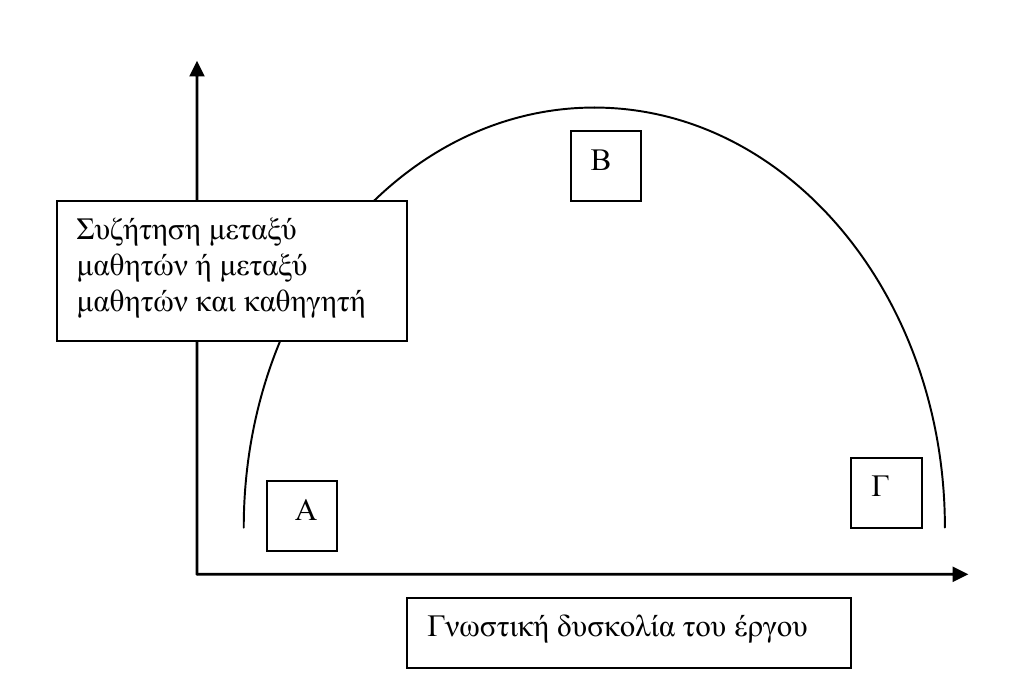
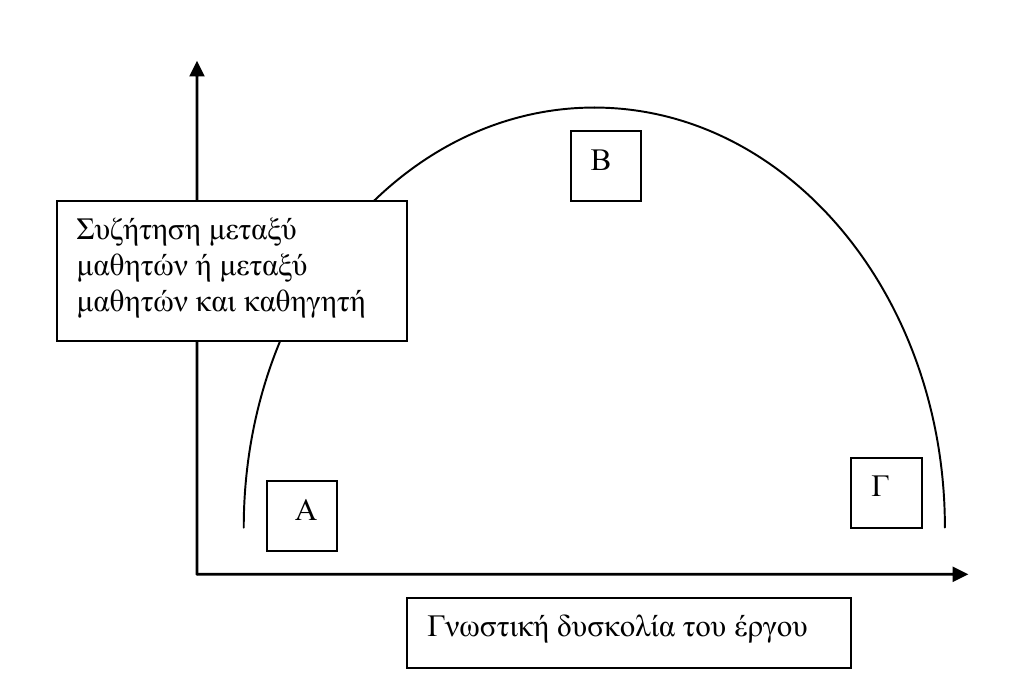
- Η Υποθετική Μαθησιακή Τροχιά
 Εισαγωγή στη Θεωρία της Διδασκαλίας
Εισαγωγή στη Θεωρία της Διδασκαλίας- Τύποι αβεβαιότητας και σχέσεις μεταξύ τους
- Αβεβαιότητα, διαπραγμάτευση, διυποκειμενικότητα (uncertainty, negotiation and intersubjectivity)
- Διαπραγμάτευση, διυποκειμενικότητα και αβεβαιότητα
- Διυποκειμενικότητα, αβεβαιότητα και διαπραγμάτευση
- Το νόημα
- Αναγνώριση και επίλυση της αβεβαιότητας στην τάξη
- Η πρακτική της τάξης (classroom practice)
- Δάσκαλος, μαθητές και η πρακτική της τάξης
- Διδάσκοντας ανάμεσα στα θρανία
Παρουσίαση Πρακτικών Ασκήσεων απο φοιτητές του μαθήματος και επεξήγηση του πειράματός τους.
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -