Μεταπτυχιακή Ανάλυση II
Σοφοκλής Μερκουράκης
Στόχος του μαθήματος είναι να παρουσιάσει βασικά αποτελέσματα της Συναρτησιακής Ανάλυσης με έμφαση στους κλασικούς χώρους.
Ενδεικτικά θέματα:
- Χώροι πηλίκα
- Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα
- Τοπολογικοί διανυσματικοί χώροι
- Τοπικά κυρτοί χώροι - βασικές ιδιότητες
- Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
- Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
- Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους - Διαχωριστικό θεώρημα Hahn-Banach
- Ασθενείς τοπολογίες σε χώρους με νόρμα - Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine - Αυτοπάθεια και ασθενής συμπάγεια
- Το θεώρημα Krein-Milman - Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
Λιγότερα
Στόχος του μαθήματος είναι να παρουσιάσει βασικά αποτελέσματα της Συναρτησιακής Ανάλυσης με έμφαση στους κλασικούς χώρους.
Ενδεικτικά θέματα:
- Χώροι πηλίκα
- Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα
- Τοπολογικοί διανυσματικοί χώροι
- Τοπικά κυρτοί χώροι - βασικές ιδιότητες
- Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
- Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
- Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους - Διαχωριστικό θεώρημα Hahn-Banach
- Ασθενείς τοπολογίες σε χώρους με νόρμα - Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine - Αυτοπάθεια και ασθενής συμπάγεια
- Το θεώρημα Krein-Milman - Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
Στόχος του μαθήματος είναι να παρουσιάσει βασικά αποτελέσματα της Συναρτησιακής Ανάλυσης με έμφαση στους κλασικούς χώρους.
Ενδεικτικά θέματα:
- Χώροι πηλίκα
- Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα
- Τοπολογικοί διανυσματικοί χώροι
- Τοπικά κυρτοί χώροι - βασικές ιδιότητες
- Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
- Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
- Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους - Διαχωριστικό θεώρημα Hahn-Banach
- Ασθενείς τοπολογίες σε χώρους με νόρμα - Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine - Αυτοπάθεια και ασθενής συμπάγεια
- Το θεώρημα Krein-Milman - Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
Περίγραμμα

Περιεχόμενο μαθήματος
- Χώροι πηλίκα
- Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα
- Τοπολογικοί διανυσματικοί χώροι
3.1 Βασικές έννοιες και ορισμοί
3.2 Τοπικά κυρτοί χώροι - βασικές ιδιότητες
3.3 Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
3.4 Παραδείγματα - Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
3.5 Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους - Διαχωριστικό θεώρημα Hahn-Banach
- Ασθενείς τοπολογίες σε χώρους με νόρμα
4.1 Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine ...
4.2 Αυτοπάθεια και ασθενής συμπάγεια
- Το θεώρημα Krein-Milman – Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
- Παραρτήματα
Διδάσκοντες
Μερκουράκης Σοφοκλής
Θέση: Καθηγητής
Ερευνητικά Ενδιαφέροντα: Χώροι Banach, Θεωρία Μέτρου, Γενική Τοπολογία, Uniform Distribution of Sequences
E-mail: smercour@math.uoa.gr
Ομάδα στόχος
Μεταπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Βιβλιογραφία
- [Α] Σ. Αργυρός, Σημειώσεις παραδόσεων Συναρτησιακής Ανάλυσης, ΣΕΜΦΕ, ΕΜΠ, Αθήνα 2004
- [Β] W.G. Bade, The Banach Space C(S), Aarhus Universitet Matematisk, Institud, 1971
- [Γ] Α. Γιαννόπουλος, Μεταπτυχιακή Ανάλυση ΙΙ, Πρόχειρες Σημειώσεις, Αθήνα, 2007
- [D] J. Diestel, Sequences and Series in Banach spaces, GTM,92,Springer, 1984
- [F-H-H-M-P-Z] M. Fabian, P. Habala, P. Hajek, J. Pelant, V. Montesinos and V. Zizler, Functional Analysis and Infinite Dimensional Geometry, CMSB in Mathematics, Springer, 2001
- [F-H-H-M-Z] M. Fabian, P. Habala, P. Hajek, V. Montesinos and V. Zizler Banach Space Theory. The basis for Linear and Nonlinear Analysis, CMSB in Mathematics, Springer, 2011
- [L – T] J. Lindenstrauss and L. Tzatriri, Classical Banach Spaces I, Sequence Spaces, Springer, 1977
- [M] R. E. Megginson, An introduction to Banach Space Theory GTM 183, Springer, 1998
- [Με] Σ. Μερκουράκης, Μεταπτυχιακή Συναρτησιακή Ανάλυση, Χειρόγραφες Σημειώσεις Παραδόσεων, Αθήνα, 1997
- [Μη] Θ. Μήτσης. Σημειώσεις Συναρτησιακής Ανάλυσης, Τμήμα Μαθηματικών Πανεπιστημίου Κρήτης
- [Ν – Ζ – Κ – Φ ] Σ. Νεγρεπόντης, Θ. Ζαχαριάδης, Ν. Καλαμίδας και Β. Φαρμάκη, Γενική Τοπολογία και Συναρτησιακή Ανάλυση, Εκδόσεις Συμμετρία, Αθήνα, 1988
- [R] W. Rudin, Functional Analysis, Mc Graw Hill, 1973
- [Τ] Λ. Τσίτσας, Μαθήματα Συναρτησιακής Ανάλυσης, Αθήνα, 1984
Σημειώματα Δικαιωμάτων Πνευματικής Ιδιοκτησίας
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Όνομα μέλους ή μελών ΔΕΠ, 2014. Σοφοκλής Μερκουράκης. Μεταπτυχιακή Ανάλυση II. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH109/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».
[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Χώροι πηλίκα
- Πεπερασμένα ευθέα αθροίσματα και προβολές σε χώρους με νόρμα
- Τοπολογικοί διανυσματικοί χώροι
3.1 Βασικές έννοιες και ορισμοί
3.2 Τοπικά κυρτοί χώροι - βασικές ιδιότητες
3.3 Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
3.4 Παραδείγματα - Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
3.5 Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους - Διαχωριστικό θεώρημα Hahn-Banach - Ασθενείς τοπολογίες σε χώρους με νόρμα
4.1 Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine ...
4.2 Αυτοπάθεια και ασθενής συμπάγεια - Το θεώρημα Krein-Milman – Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
- Παραρτήματα
Μερκουράκης Σοφοκλής
Θέση: Καθηγητής
Ερευνητικά Ενδιαφέροντα: Χώροι Banach, Θεωρία Μέτρου, Γενική Τοπολογία, Uniform Distribution of Sequences
E-mail: smercour@math.uoa.gr
Μεταπτυχιακοί φοιτητές του τμήματος Μαθηματικών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
- [Α] Σ. Αργυρός, Σημειώσεις παραδόσεων Συναρτησιακής Ανάλυσης, ΣΕΜΦΕ, ΕΜΠ, Αθήνα 2004
- [Β] W.G. Bade, The Banach Space C(S), Aarhus Universitet Matematisk, Institud, 1971
- [Γ] Α. Γιαννόπουλος, Μεταπτυχιακή Ανάλυση ΙΙ, Πρόχειρες Σημειώσεις, Αθήνα, 2007
- [D] J. Diestel, Sequences and Series in Banach spaces, GTM,92,Springer, 1984
- [F-H-H-M-P-Z] M. Fabian, P. Habala, P. Hajek, J. Pelant, V. Montesinos and V. Zizler, Functional Analysis and Infinite Dimensional Geometry, CMSB in Mathematics, Springer, 2001
- [F-H-H-M-Z] M. Fabian, P. Habala, P. Hajek, V. Montesinos and V. Zizler Banach Space Theory. The basis for Linear and Nonlinear Analysis, CMSB in Mathematics, Springer, 2011
- [L – T] J. Lindenstrauss and L. Tzatriri, Classical Banach Spaces I, Sequence Spaces, Springer, 1977
- [M] R. E. Megginson, An introduction to Banach Space Theory GTM 183, Springer, 1998
- [Με] Σ. Μερκουράκης, Μεταπτυχιακή Συναρτησιακή Ανάλυση, Χειρόγραφες Σημειώσεις Παραδόσεων, Αθήνα, 1997
- [Μη] Θ. Μήτσης. Σημειώσεις Συναρτησιακής Ανάλυσης, Τμήμα Μαθηματικών Πανεπιστημίου Κρήτης
- [Ν – Ζ – Κ – Φ ] Σ. Νεγρεπόντης, Θ. Ζαχαριάδης, Ν. Καλαμίδας και Β. Φαρμάκη, Γενική Τοπολογία και Συναρτησιακή Ανάλυση, Εκδόσεις Συμμετρία, Αθήνα, 1988
- [R] W. Rudin, Functional Analysis, Mc Graw Hill, 1973
- [Τ] Λ. Τσίτσας, Μαθήματα Συναρτησιακής Ανάλυσης, Αθήνα, 1984
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Όνομα μέλους ή μελών ΔΕΠ, 2014. Σοφοκλής Μερκουράκης. Μεταπτυχιακή Ανάλυση II. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/MATH109/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».

[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Χώροι με νόρμα
- Χώροι Banach
- Χώροι πεπερασμένης διάστασης
Λέξεις Κλειδιά: σύμπλοκο, χώρος πηλίκο, νόρμα πηλίκο, χώρος Banach, νόρμα πεπερασμένης διάστασης
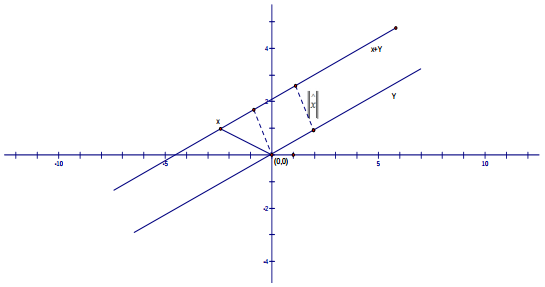
- Πεπερασμένα ευθέα αθροίσματα
- Προβολές σε χώρους με νόρμα
Λέξεις Κλειδιά: ευθύ άθροισμα, συνεχείς απεικονίσεις, συμπληρωματικός υποχώρος, φραγμένη προβολή
- Βασικές έννοιες και ορισμοί
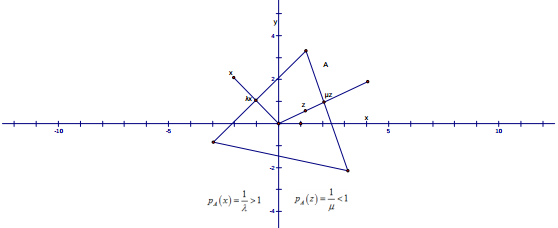
- Τοπικά κυρτοί χώροι - Βασικές ιδιότητες
- Το συναρτησοειδές του Minkowski και μετρικοποιησιμότητα σε τοπικά κυρτούς χώρους
- Παραδείγματα - Οι χώροι C(Ω), Η(Ω), C∞ ( I ) και Lp = Lp [ 0,1 ] , 0 < p < 1
- Το θεώρημα Hahn-Banach σε τοπολογικούς διανυσματικούς χώρους
Λέξεις Κλειδιά: τοπολογικός διανυσματικός χώρος, Hausdorff τοπολογικός διανυσματικός χώρος, τελεστές και συναρτησοειδή, συναρτησοειδές του Minkowski, τοπικά κυρτοί χώροι, ασθενή τοπολογία, μετρικοποιησιμότητα, θεώρημα Hahn-Banach
- Βασικά θεωρήματα: Mazur, Alaoglou, Goldstine ...
- Αυτοπάθεια και ασθενής συμπάγεια
Λέξεις Κλειδιά: ασθενείς τοπολογίες, θεώρημα Mazur, θεώρημα Alaoglou, θεώρημα Goldstine, αυτοπάθεια, ασθενής συμπάγεια
- Το θεώρημα Krein-Milman
- Βασικές ιδιότητες συμπαγών και κυρτών συνόλων
Λέξεις Κλειδιά: θεώρημα Krein-Milman, ακραία σημεία, συμπαγή και κυρτά σύνολα
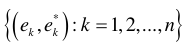
- Βάση Auerbach
- Παρατηρήσεις, ασκήσεις και διορθώσεις
Λέξεις Κλειδιά: διορθογώνιο σύστημα, βάση Auerbach
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -