Πιθανότητες II
Δημήτριος Χελιώτης
Στο μάθημα εκτίθεται αρχικά η μετροθεωρητική θεμελίωση των πιθανοτήτων. Έπειτα αναπτύσσονται εργαλεία για την απόδειξη οριακών θεωρημάτων, και με χρήση τους αποδεικνύονται τα δύο σημαντικότερα οριακά θεωρήματα της θεωρίας πιθανοτήτων, ο Νόμος των Μεγάλων Αριθμών και το Κεντρικό Οριακό Θεώρημα. Τέλος, γίνεται μια μικρή εισαγωγή στη θεωρία των μεγάλων αποκλίσεων.
Λέξεις κλειδιά: Μέτρα πιθανότητας, τυχαίες μεταβλητές, σύγκλιση τυχαίων μεταβλητών, ανεξαρτησία, ισχυρός νόμος μεγάλων αριθμών, χαρακτηριστικές συναρτήσεις, σύγκλιση κατά κατανομή, κεντρικό οριακό θεώρημα, το θεώρημα Cramer, μεγάλες αποκλίσεις.
Λιγότερα
Στο μάθημα εκτίθεται αρχικά η μετροθεωρητική θεμελίωση των πιθανοτήτων. Έπειτα αναπτύσσονται εργαλεία για την απόδειξη οριακών θεωρημάτων, και με χρήση τους αποδεικνύονται τα δύο σημαντικότερα οριακά θεωρήματα της θεωρίας πιθανοτήτων, ο Νόμος των Μεγάλων Αριθμών και το Κεντρικό Οριακό Θεώρημα. Τέλος, γίνεται μια μικρή εισαγωγή στη θεωρία των μεγάλων αποκλίσεων.
Λέξεις κλειδιά: Μέτρα πιθανότητας, τυχαίες μεταβλητές, σύγκλιση τυχαίων μεταβλητών, ανεξαρτησία, ισχυρός νόμος μεγάλων αριθμών, χαρακτηριστικές συναρτήσεις, σύγκλιση κατά κατανομή, κεντρικό οριακό θεώρημα, το θεώρημα Cramer, μεγάλες αποκλίσεις.
Στο μάθημα εκτίθεται αρχικά η μετροθεωρητική θεμελίωση των πιθανοτήτων. Έπειτα αναπτύσσονται εργαλεία για την απόδειξη οριακών θεωρημάτων, και με χρήση τους αποδεικνύονται τα δύο σημαντικότερα οριακά θεωρήματα της θεωρίας πιθανοτήτων, ο Νόμος των Μεγάλων Αριθμών και το Κεντρικό Οριακό Θεώρημα. Τέλος, γίνεται μια μικρή εισαγωγή στη θεωρία των μεγάλων αποκλίσεων.
Λέξεις κλειδιά: Μέτρα πιθανότητας, τυχαίες μεταβλητές, σύγκλιση τυχαίων μεταβλητών, ανεξαρτησία, ισχυρός νόμος μεγάλων αριθμών, χαρακτηριστικές συναρτήσεις, σύγκλιση κατά κατανομή, κεντρικό οριακό θεώρημα, το θεώρημα Cramer, μεγάλες αποκλίσεις.
Περίγραμμα

Περιεχόμενο μαθήματος
- Σ-άλγεβρες, μέτρα, μετρήσιμες συναρτήσεις, ολοκλήρωμα Lebesgue.
- Τρόποι σύγκλισης τυχαίων μεταβλητών.
- Ανεξαρτησία, τα λήμματα Borel-Cantelli, ο νόμος 0-1 του Kolmogorov.
- Ο ισχυρός νόμος των μεγάλων αριθμών.
- Χαρακτηριστικές συναρτήσεις, σύγκλιση κατά κατανομή.
- Το κεντρικό οριακό θεώρημα.
- Μεγάλες αποκλίσεις και το θεώρημα Cramer.
Μαθησιακοί στόχοι
- Φορμαλισμός Πιθανοτήτω, έννοιες και βασικές τους ιδιότητες (σ-άλγεβρα, μέτρο πιθανότητας, τυχαία μεταβλητή, μέση τιμέ, ανεξαρτησία, σύγκλιση ανολουθιών τυχαίων μεταβλητών.)
- Τεχνικές απόδειξης σχεδόν βέβαιης σύγκλισης και σύγκλισης κατά κατανομή.
- Εφαρμογή στη μελέτη του μερικού αθροίσματος S_n=X_1+X_2+...+X_n ακολουθίας ανεξάρτητων και ισόνομων τυχαίων μεταβλητών (Νόμος μεγάλων αριθμών, Κεντρικό οριακό θεώρημα).
- Εισαγωγή στη θεωρία των μεγάλων αποκλίσεων.
Προαπαιτούμενα
- Απειροστικός Ι, Απειροστικός ΙΙ.
- Πιθανότητες Ι.
- Βασικές γνώσεις πραγματικής ανάλυσης.
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών και πτυχιούχοι του τμήματος.
Βιβλιογραφία
Με αύξουσα σειρά δυσκολίας:
(1) M.Capinski,E.Kopp. Measure, Integral and Probability.
(2) J. Rosenthal. First Look at Rigorous Probability Theory.
(3) J. Jacod - P. Protter. Probability Essentials.
(4) S. Resnick. A Probability Path.
(5) D. Williams. Probability with martingales.
(6) R. Durrett. Probability. Theory and examples.
Στα Ελληνικά υπάρχουν μόνο δύο βιβλία:
(7) Σ. Καλπαζίδου. Στοιχεία Μετροθεωρίας Πιθανοτήτων.
(8) Ν. Παπαδάτος. Θεωρία Πιθανοτήτων.
Το (7) είναι συνοπτικό και επικεντρώνεται σε θέματα θεμελίωσης περισσότερο παρά σε πιθανοθεψρητικές εφαρμογές.Το (8) είναι μεταπτυχιακού πειπέδου ως πρός το περιεχμενο, αλλά πολύ αναλυτικό, γραμμένο με ύφος εισαγωγικού προπτυχιακού βιβλίου. Διατίθεται μόνο απο το συγγραφέα, δεν κυκλοφορεί στο εμπόριο.
Διδάσκοντες
Χελιώτης Δημήτριος
Θέση : Επίκουρος Καθηγητής
Ερευνητικά Ενδιαφέροντα : Θεωρία Πιθανοτήτων
- Σ-άλγεβρες, μέτρα, μετρήσιμες συναρτήσεις, ολοκλήρωμα Lebesgue.
- Τρόποι σύγκλισης τυχαίων μεταβλητών.
- Ανεξαρτησία, τα λήμματα Borel-Cantelli, ο νόμος 0-1 του Kolmogorov.
- Ο ισχυρός νόμος των μεγάλων αριθμών.
- Χαρακτηριστικές συναρτήσεις, σύγκλιση κατά κατανομή.
- Το κεντρικό οριακό θεώρημα.
- Μεγάλες αποκλίσεις και το θεώρημα Cramer.
- Φορμαλισμός Πιθανοτήτω, έννοιες και βασικές τους ιδιότητες (σ-άλγεβρα, μέτρο πιθανότητας, τυχαία μεταβλητή, μέση τιμέ, ανεξαρτησία, σύγκλιση ανολουθιών τυχαίων μεταβλητών.)
- Τεχνικές απόδειξης σχεδόν βέβαιης σύγκλισης και σύγκλισης κατά κατανομή.
- Εφαρμογή στη μελέτη του μερικού αθροίσματος S_n=X_1+X_2+...+X_n ακολουθίας ανεξάρτητων και ισόνομων τυχαίων μεταβλητών (Νόμος μεγάλων αριθμών, Κεντρικό οριακό θεώρημα).
- Εισαγωγή στη θεωρία των μεγάλων αποκλίσεων.
- Απειροστικός Ι, Απειροστικός ΙΙ.
- Πιθανότητες Ι.
- Βασικές γνώσεις πραγματικής ανάλυσης.
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών και πτυχιούχοι του τμήματος.
Με αύξουσα σειρά δυσκολίας:
(1) M.Capinski,E.Kopp. Measure, Integral and Probability.
(2) J. Rosenthal. First Look at Rigorous Probability Theory.
(3) J. Jacod - P. Protter. Probability Essentials.
(4) S. Resnick. A Probability Path.
(5) D. Williams. Probability with martingales.
(6) R. Durrett. Probability. Theory and examples.
Στα Ελληνικά υπάρχουν μόνο δύο βιβλία:
(7) Σ. Καλπαζίδου. Στοιχεία Μετροθεωρίας Πιθανοτήτων.
(8) Ν. Παπαδάτος. Θεωρία Πιθανοτήτων.
Το (7) είναι συνοπτικό και επικεντρώνεται σε θέματα θεμελίωσης περισσότερο παρά σε πιθανοθεψρητικές εφαρμογές.Το (8) είναι μεταπτυχιακού πειπέδου ως πρός το περιεχμενο, αλλά πολύ αναλυτικό, γραμμένο με ύφος εισαγωγικού προπτυχιακού βιβλίου. Διατίθεται μόνο απο το συγγραφέα, δεν κυκλοφορεί στο εμπόριο.
Χελιώτης Δημήτριος
Θέση : Επίκουρος Καθηγητής
Ερευνητικά Ενδιαφέροντα : Θεωρία Πιθανοτήτων
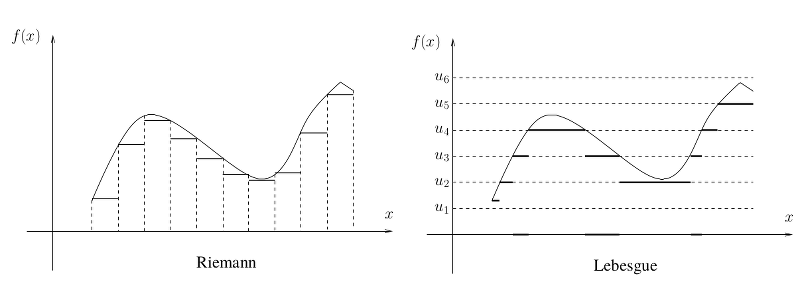
- Σ-άλγεβρες, Τα σύνολα Borel
- Μέτρα, Το θεώρημα π-λ
- Μετρήσιμες συναρτήσεις
- Το ολοκλήρωμα Lebesgue, Οι χώροι L^p
- Τα βασικά οριακά θεωρήματα
- Κατανομή τυχαίας μεταβλητής και ολοκλήρωση, Είδη κατανομών στο R
- Τρόποι σύγκλισης τυχαίων μεταβλητών
- Μέτρα γινόμενο, Tο θεώρημα Fubini
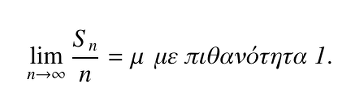
- Ανεξαρτησία για οικογένειες συνόλων και για τυχαίες μεταβλητές
- Κατασκευή ανεξάρτητων τυχαίων μεταβλητών με δεδομένη κατανομή
- Τα λήμματα Borel-Cantelli
- Ο νόμος 0-1 του Kolmogorov
- Ο ισχυρός νόμος των μεγάλων αριθμών
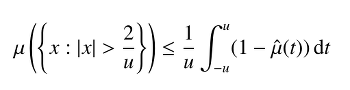
- Χαρακτηριστικές συναρτήσεις
- Ροπογεννήτριες και η σχέση τους με τις χαρακτηριστικές συναρτήσεις
- Άθροισμα ανεξάρτητων τυχαίων μεταβλητών
- Σύγκλιση κατά κατανομή, Σφιχτότητα
- Το θεώρημα συνέχειας του Levy και εφαρμογές του
- Το κεντρικό οριακό θεώρημα
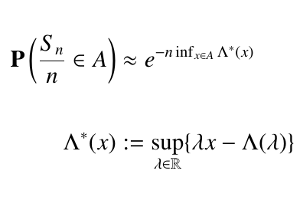
- Η έννοια της μεγάλης απόκλισης και ο ρόλος της στην ασυμπτωτική θεωρία
- Η αρχή μεγάλων αποκλίσεων
- Το Θεώρημα Cramer
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -

