Κυρτή Ανάλυση
Λεώνη Ευαγγελάτου-Δάλλα
Το μάθημα παρουσιάζει βασικά αποτελέσματα της Κυρτής Γεωμετρικής Ανάλυσης. Τα αντικείμενα που θα μελετήσουμε είναι (κυρίως) κυρτά σώματα: συμπαγή και κυρτά υποσύνολα του n-διάστατου Ευκλείδειου χώρου, τα οποία έχουν μη κενό εσωτερικό.
Η κυρτότητα παίζει σημαντικό ρόλο σε πολλές περιοχές των Μαθηματικών: στη συναρτησιακή ανάλυση, στις μερικές διαφορικές εξισώσεις, στο γραμμικό προγραμματισμό, στη θεωρία πιθανοτήτων και τη θεωρία πληροφορίας, στη γεωμετρία των αριθμών. Δεύτερος στόχος του μαθήματος είναι να παρουσιάσει έναν όσο γίνεται μεγαλύτερο αριθμό από αυτές τις διασυνδέσεις. Ένας τρίτος στόχος του μαθήματος είναι να ενισχύσει τη διαίσθηση για τη μετρική και τον όγκο στις μεγάλες διαστάσεις.
- Κυρτά σύνολα. Κυρτές, κοίλες συναρτήσεις.
- Θεωρήματα Καραθεοδωρή, Helly, Radon. Εφαρμογές στη συνδυαστική γεωμετρία και τη θεωρία προσέγγισης.
- Μετρική προβολή. Φέροντα υπερεπίπεδα. Διαχωριστικά θεωρήματα. Δυϊσμός. Συνάρτηση στήριξης.
- Ακραία και εκτεθειμένα σημεία. Το θεώρημα των Minkowski-Krein-Milman. Εφαρμογές (πολύτοπο του Birkhoff, πολύτοπα μεταθέσεων, ανισότητες για ιδιοτιμές πινάκων).
- Μετρική Hausdorff. Το θεώρημα επιλογής του Blaschke. Συμμετρικοποίηση κατά Steiner. Γεωμετρικές ανισότητες.
- Όγκος στον n-διάστατο Ευκλείδειο χώρο. Παράδοξα στις μεγάλες διαστάσεις.
- Ανισότητα Brunn-Minkowski. Ισοπεριμετρικά προβλήματα.
- Ειδικά θέματα (γεωμετρικές ανισότητες, γεωμετρία των αριθμών, χώροι πεπερασμένης διάστασης με νόρμα, ελλειψοειδή και αλγόριθμοι για τον υπολογισμό του όγκου, γεωμετρικές πιθανότητες).
Λιγότερα
Το μάθημα παρουσιάζει βασικά αποτελέσματα της Κυρτής Γεωμετρικής Ανάλυσης. Τα αντικείμενα που θα μελετήσουμε είναι (κυρίως) κυρτά σώματα: συμπαγή και κυρτά υποσύνολα του n-διάστατου Ευκλείδειου χώρου, τα οποία έχουν μη κενό εσωτερικό.
Η κυρτότητα παίζει σημαντικό ρόλο σε πολλές περιοχές των Μαθηματικών: στη συναρτησιακή ανάλυση, στις μερικές διαφορικές εξισώσεις, στο γραμμικό προγραμματισμό, στη θεωρία πιθανοτήτων και τη θεωρία πληροφορίας, στη γεωμετρία των αριθμών. Δεύτερος στόχος του μαθήματος είναι να παρουσιάσει έναν όσο γίνεται μεγαλύτερο αριθμό από αυτές τις διασυνδέσεις. Ένας τρίτος στόχος του μαθήματος είναι να ενισχύσει τη διαίσθηση για τη μετρική και τον όγκο στις μεγάλες διαστάσεις.
- Κυρτά σύνολα. Κυρτές, κοίλες συναρτήσεις.
- Θεωρήματα Καραθεοδωρή, Helly, Radon. Εφαρμογές στη συνδυαστική γεωμετρία και τη θεωρία προσέγγισης.
- Μετρική προβολή. Φέροντα υπερεπίπεδα. Διαχωριστικά θεωρήματα. Δυϊσμός. Συνάρτηση στήριξης.
- Ακραία και εκτεθειμένα σημεία. Το θεώρημα των Minkowski-Krein-M
Το μάθημα παρουσιάζει βασικά αποτελέσματα της Κυρτής Γεωμετρικής Ανάλυσης. Τα αντικείμενα που θα μελετήσουμε είναι (κυρίως) κυρτά σώματα: συμπαγή και κυρτά υποσύνολα του n-διάστατου Ευκλείδειου χώρου, τα οποία έχουν μη κενό εσωτερικό.
Η κυρτότητα παίζει σημαντικό ρόλο σε πολλές περιοχές των Μαθηματικών: στη συναρτησιακή ανάλυση, στις μερικές διαφορικές εξισώσεις, στο γραμμικό προγραμματισμό, στη θεωρία πιθανοτήτων και τη θεωρία πληροφορίας, στη γεωμετρία των αριθμών. Δεύτερος στόχος του μαθήματος είναι να παρουσιάσει έναν όσο γίνεται μεγαλύτερο αριθμό από αυτές τις διασυνδέσεις. Ένας τρίτος στόχος του μαθήματος είναι να ενισχύσει τη διαίσθηση για τη μετρική και τον όγκο στις μεγάλες διαστάσεις.
- Κυρτά σύνολα. Κυρτές, κοίλες συναρτήσεις.
- Θεωρήματα Καραθεοδωρή, Helly, Radon. Εφαρμογές στη συνδυαστική γεωμετρία και τη θεωρία προσέγγισης.
- Μετρική προβολή. Φέροντα υπερεπίπεδα. Διαχωριστικά θεωρήματα. Δυϊσμός. Συνάρτηση στήριξης.
- Ακραία και εκτεθειμένα σημεία. Το θεώρημα των Minkowski-Krein-M
Περίγραμμα

Περιεχόμενο μαθήματος
- Κυρτά σύνολα. Κυρτές, κοίλες συναρτήσεις.
- Θεωρήματα Καραθεοδωρή, Helly, Radon. Εφαρμογές στη συνδυαστική γεωμετρία και τη θεωρία προσέγγισης.
- Μετρική προβολή. Φέροντα υπερεπίπεδα. Διαχωριστικά θεωρήματα. Δυϊσμός. Συνάρτηση στήριξης.
- Ακραία και εκτεθειμένα σημεία. Το θεώρημα των Minkowski-Krein-Milman. Εφαρμογές (πολύτοπο του Birkhoff, πολύτοπα μεταθέσεων, ανισότητες για ιδιοτιμές πινάκων).
- Μετρική Hausdorff. Το θεώρημα επιλογής του Blaschke. Συμμετρικοποίηση κατά Steiner. Γεωμετρικές ανισότητες.
- Όγκος στον n-διάστατο Ευκλείδειο χώρο. Παράδοξα στις μεγάλες διαστάσεις.
- Ανισότητα Brunn-Minkowski. Ισοπεριμετρικά προβλήματα.
- Ειδικά θέματα (γεωμετρικές ανισότητες, γεωμετρία των αριθμών, χώροι πεπερασμένης διάστασης με νόρμα, ελλειψοειδή και αλγόριθμοι για τον υπολογισμό του όγκου, γεωμετρικές πιθανότητες).
Διδάσκοντες
Λεώνη Ευαγγελάτου-Δάλλα
Θέση: Αναπληρώτρια Καθηγήτρια
Ερευνητικά ενδιαφέροντα: Κυρτότητα, Fractals
e-mail: ldalla@math.uoa.gr
Τηλέφωνο: 210-7276375
Fax: 210-7276378
Γραφείο: 207
Μαθησιακοί στόχοι
- Η παρουσίαση των βασικών αποτελεσμάτων της Κυρτής Γεωμετρικής Ανάλυσης.
- Η παρουσίαση των περισσότερων διασυνδέσεων της έννοιας της κυρτότητας με άλλες περιοχές των Μαθηματικών.
- Η ενίσχυση της διαίσθησης για τις έννοιες της μετρικής και του όγκου, στις μεγάλες διαστάσεις.
Προαπαιτούμενα
- Απειροστικός Λογισμός Ι,ΙΙ και ΙΙΙ
- Γραμμική Άλγεβρα Ι και ΙΙ
Ομάδα στόχος
Προπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Θεωρητικά Μαθηματικά – Μαθηματική Ανάλυση”.
Προτεινόμενα συγγράμματα
Απόστολος Γιαννόπουλος - “Σημειώσεις Κυρτής Ανάλυσης”, 2009.
Βιβλιογραφία
- K. Ball: An elementary introduction to modern convex geometry.
- A. Barvinok: A course in convexity.
- Υ. D. Burago and V. A. Zalgaller: Geometric Inequalities.
- H. G. Eggleston: Convexity.
- P. Gruber: Convex and Discrete Geometry.
- D. A. Klain and G-C Rota: Introduction to geometric probability.
- J. Matousek: Lectures on discrete geometry
- V. D. Milman and G. Schechtman: Asymptotic theory of finite dimensional normed spaces.
- R. Schneider: Convex bodies - the Brunn-Minkowski theory.
- R. J. Webster: Convexity.
- Κυρτά σύνολα. Κυρτές, κοίλες συναρτήσεις.
- Θεωρήματα Καραθεοδωρή, Helly, Radon. Εφαρμογές στη συνδυαστική γεωμετρία και τη θεωρία προσέγγισης.
- Μετρική προβολή. Φέροντα υπερεπίπεδα. Διαχωριστικά θεωρήματα. Δυϊσμός. Συνάρτηση στήριξης.
- Ακραία και εκτεθειμένα σημεία. Το θεώρημα των Minkowski-Krein-Milman. Εφαρμογές (πολύτοπο του Birkhoff, πολύτοπα μεταθέσεων, ανισότητες για ιδιοτιμές πινάκων).
- Μετρική Hausdorff. Το θεώρημα επιλογής του Blaschke. Συμμετρικοποίηση κατά Steiner. Γεωμετρικές ανισότητες.
- Όγκος στον n-διάστατο Ευκλείδειο χώρο. Παράδοξα στις μεγάλες διαστάσεις.
- Ανισότητα Brunn-Minkowski. Ισοπεριμετρικά προβλήματα.
- Ειδικά θέματα (γεωμετρικές ανισότητες, γεωμετρία των αριθμών, χώροι πεπερασμένης διάστασης με νόρμα, ελλειψοειδή και αλγόριθμοι για τον υπολογισμό του όγκου, γεωμετρικές πιθανότητες).
Λεώνη Ευαγγελάτου-Δάλλα
Θέση: Αναπληρώτρια Καθηγήτρια
Ερευνητικά ενδιαφέροντα: Κυρτότητα, Fractals
e-mail: ldalla@math.uoa.gr
Τηλέφωνο: 210-7276375
Fax: 210-7276378
Γραφείο: 207
- Η παρουσίαση των βασικών αποτελεσμάτων της Κυρτής Γεωμετρικής Ανάλυσης.
- Η παρουσίαση των περισσότερων διασυνδέσεων της έννοιας της κυρτότητας με άλλες περιοχές των Μαθηματικών.
- Η ενίσχυση της διαίσθησης για τις έννοιες της μετρικής και του όγκου, στις μεγάλες διαστάσεις.
- Απειροστικός Λογισμός Ι,ΙΙ και ΙΙΙ
- Γραμμική Άλγεβρα Ι και ΙΙ
Προπτυχιακοί φοιτητές του Τμήματος Μαθηματικών, ενδιαφερόμενοι για τη θεματική περιοχή “Θεωρητικά Μαθηματικά – Μαθηματική Ανάλυση”.
Απόστολος Γιαννόπουλος - “Σημειώσεις Κυρτής Ανάλυσης”, 2009.
- K. Ball: An elementary introduction to modern convex geometry.
- A. Barvinok: A course in convexity.
- Υ. D. Burago and V. A. Zalgaller: Geometric Inequalities.
- H. G. Eggleston: Convexity.
- P. Gruber: Convex and Discrete Geometry.
- D. A. Klain and G-C Rota: Introduction to geometric probability.
- J. Matousek: Lectures on discrete geometry
- V. D. Milman and G. Schechtman: Asymptotic theory of finite dimensional normed spaces.
- R. Schneider: Convex bodies - the Brunn-Minkowski theory.
- R. J. Webster: Convexity.
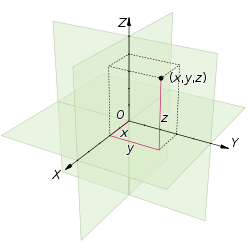
- Ευκλείδειος χώρος
- Η ανισότητα Brunn-Minkowski
- Η ισοπεριμετρική ανισότητα
- Όγκος και διάσταση
Λέξεις κλειδιά: Ευκλείδειος χώρος, νόρμα, κυρτό σύνολο, σώμα, όγκος, ανισότητα, Brunn, Minkowski, ισοπεριμετρική, διάσταση, συνάρτηση Γάμμα, τύπος Stirling
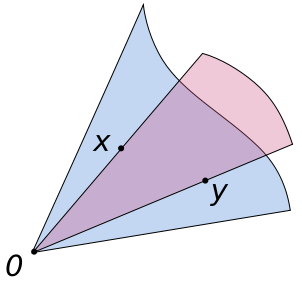
- Κυρτή θήκη
- Το θεώρημα του Καραθεοδωρή
- Τα θεωρήματα των Radon και Helly
- Εφαρμογές στη συνδυαστική γεωμετρία
- Γενικεύσεις των τριών θεωρημάτων
Λέξεις κλειδιά: κυρτή θήκη, κυρτός συνδυασμός, κυρτό σώμα, πολύτοπο, πολύεδρο, λεξικογραφική διάταξη, κυρτός κώνος, θεώρημα Tverberg
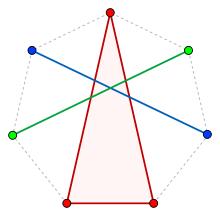
- Το θεώρημα του Minkowski
- Εφαρμογές στη θεωρία των αριθμών
- Ακέραια σημεία σε ελλειψοειδή
Λέξεις κλειδιά: θεώρημα Minkowski, κυρτό σώμα, νόρμα, γραμμικές μορφές, τετραγωνικές μορφές, ελλειψοειδές, ακέραια σημεία, όγκος, ισοπεριμετρική ανισότητα
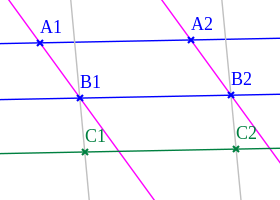
- Αφινική θήκη και αφινική διάσταση
- Τοπολογικές ιδιότητες κυρτών συνόλων
- Μετρική προβολή
- Υπερεπίπεδα στήριξης και διαχωριστικά θεωρήματα
- Πολικό συνόλου
Λέξεις κλειδιά: αφινικός συνδυασμός, αφινική, θήκη, διάσταση, ανεξαρτησία, βαρυκεντρικές συντεταγμένες, σχετικό, εσωτερικό, σύνορο, k-simplex, μετρική προβολή, υπερεπίπεδα στήριξης, διαχωριστικά θεωρήματα, πολικό συνόλου
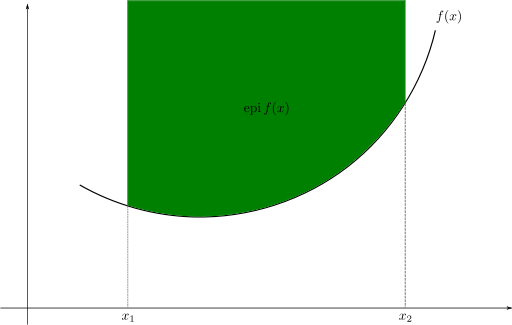
- Κυρτές συναρτήσεις μίας μεταβλητής
- Κυρτές συναρτήσεις πολλών μεταβλητών
- Συνάρτηση στήριξης και συνάρτηση στάθμης
Λέξεις κλειδιά: συνάρτηση, κυρτή, κοίλη, επιγράφημα, συνέχεια, Lipschitz, αφινική, διαφορίσιμη, στήριξης, στάθμης, νόρμα

- Ακραία και εκτεθειμένα σημεία
- Πολύτοπα και πολύεδρα
- Το πολύτοπο του Birkhoff
Λέξεις κλειδιά: σημεία, ακραία, εκτεθειμένα, σύνολο, κυρτό, συμπαγές, πολύτοπο, πολύεδρο, Birkhoff, ιδιοτιμές, ανισότητα, Hadamard, Minkowski
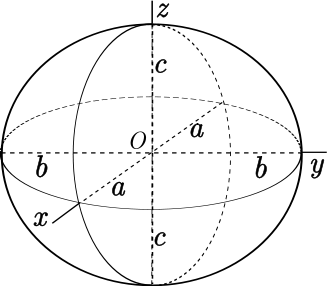
- Απόσταση Banach-Mazur
- Το λήμμα του Auerbach
- Το Banach-Mazur compactum
- Ελλειψοειδές μέγιστου όγκου ενός κυρτού σώματος
- Το θεώρημα του John
- Σημεία επαφής και η αναπαράσταση της ταυτοτικής απεικόνισης
- Λήμματα Dvoretzky-Rogers
Λέξεις κλειδιά: τελεστής, φραγμένος, νόρμα, απόσταση, Banach, Mazur, διορθογώνιο σύστημα, λήμμα, Auerbach, compactum, ελλειψοειδές, μέγιστου όγκου, θεώρημα John, σημείο επαφής, ακτινική συνάρτηση, Dvoretzky, Rogers
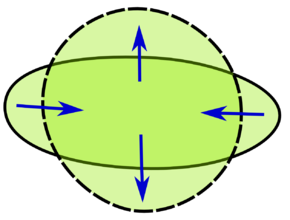
- Ισοπεριμετρική ανισότητα στη σφαίρα
- Το θεώρημα του Dvoretzky
Λέξεις κλειδιά: λήμμα, Dvoretzky, Rogers, θεώρημα, ισοπεριμετρική ανισότητα, σφαίρα, μέτρο, πιθανότητας, συνέχειας, μέσος Lévy, δ-δίκτυο, ελλειψοειδές
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -