Πληροφορική Ι (MATH361)
Μιχάλης Δρακόπουλος
Εισαγωγή στον προγραμματισμό και στην αλγοριθμική επίλυση προβλημάτων με το MATLAB.
Introduction to programming and algorithmic problem solving with MATLAB.
Λιγότερα
Εισαγωγή στον προγραμματισμό και στην αλγοριθμική επίλυση προβλημάτων με το MATLAB.
Introduction to programming and algorithmic problem solving with MATLAB.
Εισαγωγή στον προγραμματισμό και στην αλγοριθμική επίλυση προβλημάτων με το MATLAB.
Introduction to programming and algorithmic problem solving with MATLAB.
Περίγραμμα
Περιεχόμενο μαθήματος
Αλγοριθμική επίλυση προβλημάτων και προγραμματισμός με MATLAB.
Μερικά από τα θέματα που θα καλυφθούν περιλαμβάνουν:
- Βασικές έννοιες υπολογιστών και αλγορίθμων.
- Μεταβλητές, τελεστές/εκφράσεις, αναθέσεις, είσοδος/έξοδος.
- Εντολές ελέγχου και επανάληψης.
- Συναρτήσεις, αναδρομή.
- Πίνακες/διανύσματα και βασικές δομές δεδομένων.
- Αναζήτηση/ταξινόμηση, αποτελεσματικότητα αλγορίθμων.
- Υπολογιστική αναπαράσταση αριθμών.
- Μαθηματικές εφαρμογές, προσομοίωση/μοντελοποίηση, γραφικά.
----------------------------------------------------------------------------------------------------------------------------------------------------------
Some of the topics to be covered include:
- Basic computer concepts and algorithms.
- Variables, operators / expressions, assignments, input / output.
- Commands control and recurrence.
- Functions, recursion.
- Tables / vectors and basic data structures.
- Search / classification algorithms efficiency.
- Computational representation of numbers.
- Mathematical applications, simulation / modeling, graphics.
- Algorithmic problem solving and programming in MATLAB.
Μαθησιακοί στόχοι
Η διδασκαλία περιλαμβάνει 4 ώρες θεωρίας την εβδομάδα και 2 ώρες εργαστηρίου.Τα εργαστήρια είναι προαιρετικά, δεν βαθμολογούνται και απευθύνονται στους φοιτητές (όλων των ετών) που επιθυμούν να κάνουν πρακτική εξάσκηση σε μέρος της ύλης που διδάσκονται στη θεωρία (δείτε τον τρόπο επιλογής εργαστηρίου παρακάτω).
Τρόπος επιλογής εργαστηρίου
Τα εργαστήρια του μαθήματος είναι προαιρετικά και ΔΕΝ βαθμολογούνται. Απευθύνονται σε όλους τους φοιτητές του μαθήματος, ανεξαρτήτως έτους.
Πριν από την έναρξη της κάθε εργαστηριακής εβδομάδας ανακοινώνεται το περιεχόμενο του επικείμενου εργαστηριακού μαθήματος στην eclass.
Τα εργαστήρια λειτουργούν συμπληρωματικά της θεωρίας και έχουν ως βασικό στόχο την εξάσκηση των φοιτητών στον προγραμματισμό ώστε να κατανοηθούν καλύτερα κάποιες από τις έννοιες του θεωρητικού μέρους του μαθήματος. Σκοπός είναι να παρακολουθούν τα εργαστήρια οι φοιτητές που πραγματικά πιστεύουν ότι έχουν την ανάγκη πρακτικής εξάσκησης και επιπλέον βοήθειας από τους βοηθούς των εργαστηρίων. Δεν υπάρχει κάποια βαθμολογική ενίσχυση για όσους παρακολουθήσουν τα εργαστήρια. Ο στόχος τους είναι καθαρά βοηθητικός ως προς την εξάσκηση στον προγραμματισμό.
Ύλη των εργαστηριακών μαθημάτων (ενδέχεται να τροποποιηθεί):
Εργαστήριο 1: Εισαγωγή στη χρήση του MATLAB/Octave
Εργαστήριο 2: Λογικές πράξεις / Έλεγχος συνθηκών
Εργαστήριο 3: Επαναληπτικές διαδικασίες
Εργαστήριο 4: Συναρτήσεις
Εργαστήριο 5: Διανύσματα
Εργαστήριο 6: Πίνακες
Εργαστήριο 7: Αλγόριθμοι, αναδρομή
Εργαστήριο 8: Μαθηματικές εφαρμογές
Επιπλέον συνιστώμενη βιβλιογραφία
MATLAB και συμβατά προγράμματα:
- The Mathworks:
Η επίσημη ιστοσελίδα του MATLAB
- MATLAB (Wikipedia):
Άρθρο στη Wikipedia για το MATLAB, με πολλούς συνδέσμους σε εισαγωγικές και προχωρημένες σημειώσεις, και άλλες πληροφορίες.
http://en.wikipedia.org/wiki/MATLAB
- GNU Octave:
Κλώνος του MATLAB (ανοιχτό λογισμικό)
http://www.gnu.org/software/octave/
- GNU Octave (Wikipedia):
Άρθρο στη Wikipedia για το Octave και συμβατότητά του με το MATLAB
http://en.wikipedia.org/wiki/GNU_Octave
- Octave wiki:
http://wiki.octave.org/Main_Page
- Σημειώσεις MATLAB στο web
ΠΡΟΣΟΧΗ: Οι σημειώσεις αυτές είναι για προχωρημένους και θα είναι χρήσιμες όταν καλυφθεί η βασική ύλη στο μάθημα.
- A practical introduction to MATLAB (M. S. Gockenbach)
- An introduction to MATLAB (D. F. Griffiths)
Youtube videos
- Gates, M. Zuckerberg, C. Bosh campaign for more programmers
https://www.youtube.com/watch?v=nKIu9yen5nc#t=18
Ομιλία Steve Jobs στο Stanford
Μέθοδοι διδασκαλίας
- Διδασκαλία καθ΄ έδρας και συμπληρωματική-ενισχυτική εκπαίδευση μέσω ασύγχρονης πλατφόρμας.
- Εργαστήριο.
----------------------------------------------------------------------------------------------------------------------------------------------------------
- Teaching from the chair and complementary-support training via asynchronous platform.
- Laboratory
Μέθοδοι αξιολόγησης
Εξετάσεις
-----------------------------------------------------------------------------------------
Examinations
Προαπαιτούμενα
Το μάθημα είναι πρώτου εξαμήνου και δεν έχει προαπαιτούμενα
---------------------------------------------------------------------------------------
This course is the first semester and has no prerequisites
Διδάσκοντες
Δρακόπουλος Μιχάλης
Επίκουρος Καθηγητής
Ερευνητικά Ενδιαφέροντα : Υπολογιστική Επιστήμη, Παράλληλη Επεξεργασία, Πεπερασμένα Στοιχεία, Αριθμητική Βελτιστοποίηση.
e-mail : mdraco@math.uoa.gr
Προσωπική Ιστοσελίδα:
http://users.uoa.gr/~mdraco/
----------------------------------------------------------------------------------------------------------------------------------------------------------
Michael C. Dracopoulos
Dept. of Mathematics, University of Athens
Panepistimioupolis, 157 84 Athens, Greece
e-mail : mdraco@math.uoa.gr
Background
- Diploma in Civil Engineering, National Technical University of Athens, 1989.
- PhD (Computational Mathematics/Mechanics), Imperial College, London, 1993.
- ERCIM Fellow at RAL, Oxon and CWI, Amsterdam, 1993--1994.
- Research Officer, Oxford University Computing Laboratory, 1994--1997.
- Lecturer, Dept. of Mathematics, University of Athens, 1999--2003.
- Assistant Professor, Dept. of Mathematics, University of Athens, 2003--present.
Research
Scientific and parallel computing, numerical analysis, finite elements, numerical optimization, simulation and modelling.
Publications
Teaching
- Computer Science I (UG, Fall Term)
- Computational Mathematics I (PG, Fall Term)
- Computer Science II (UG, Spring Term)
- Computational Science and Technology (PG, Spring Term)
Publications
http://users.uoa.gr/~mdraco/publications.html
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών.
----------------------------------------------------------------------------------------------
Undergraduate students of University of Athens Department of Mathematics
Προτεινόμενα συγγράμματα
Βοηθήματα:
- C.F. van Loan & K.-Y.D. Fan. Το MATLAB στην Υπολογιστική Επιστήμη και Τεχνολογία - Μια Εισαγωγή. Εκδόσεις DaVinci, 2012.
- Γ. Γραββάνης & Κ. Γιαννουτάκης. Προγραμματισμός με τη χρήση MATLAB. Εκδόσεις Παπασωτηρίου, 2012.
Περισσότερα
- Ώρες γραφείου: Μετά από συνεννόηση (email)
- Διαλέξεις: 2 φορές την εβδομάδα, από 2 ώρες
- Εργαστήρια: 2 ώρες την εβδομάδα
----------------------------------------------------------------------------------------------------------------------------------------------------------
- Office hours: After agreement (email)
- Lectures: 2 times a week, 2 hours
- Laboratory: 2 hours per week
Αλγοριθμική επίλυση προβλημάτων και προγραμματισμός με MATLAB.
Μερικά από τα θέματα που θα καλυφθούν περιλαμβάνουν:
- Βασικές έννοιες υπολογιστών και αλγορίθμων.
- Μεταβλητές, τελεστές/εκφράσεις, αναθέσεις, είσοδος/έξοδος.
- Εντολές ελέγχου και επανάληψης.
- Συναρτήσεις, αναδρομή.
- Πίνακες/διανύσματα και βασικές δομές δεδομένων.
- Αναζήτηση/ταξινόμηση, αποτελεσματικότητα αλγορίθμων.
- Υπολογιστική αναπαράσταση αριθμών.
- Μαθηματικές εφαρμογές, προσομοίωση/μοντελοποίηση, γραφικά.
----------------------------------------------------------------------------------------------------------------------------------------------------------
Some of the topics to be covered include:
- Basic computer concepts and algorithms.
- Variables, operators / expressions, assignments, input / output.
- Commands control and recurrence.
- Functions, recursion.
- Tables / vectors and basic data structures.
- Search / classification algorithms efficiency.
- Computational representation of numbers.
- Mathematical applications, simulation / modeling, graphics.
- Algorithmic problem solving and programming in MATLAB.
Η διδασκαλία περιλαμβάνει 4 ώρες θεωρίας την εβδομάδα και 2 ώρες εργαστηρίου.Τα εργαστήρια είναι προαιρετικά, δεν βαθμολογούνται και απευθύνονται στους φοιτητές (όλων των ετών) που επιθυμούν να κάνουν πρακτική εξάσκηση σε μέρος της ύλης που διδάσκονται στη θεωρία (δείτε τον τρόπο επιλογής εργαστηρίου παρακάτω).
Τρόπος επιλογής εργαστηρίου
Τα εργαστήρια του μαθήματος είναι προαιρετικά και ΔΕΝ βαθμολογούνται. Απευθύνονται σε όλους τους φοιτητές του μαθήματος, ανεξαρτήτως έτους.
Πριν από την έναρξη της κάθε εργαστηριακής εβδομάδας ανακοινώνεται το περιεχόμενο του επικείμενου εργαστηριακού μαθήματος στην eclass.
Τα εργαστήρια λειτουργούν συμπληρωματικά της θεωρίας και έχουν ως βασικό στόχο την εξάσκηση των φοιτητών στον προγραμματισμό ώστε να κατανοηθούν καλύτερα κάποιες από τις έννοιες του θεωρητικού μέρους του μαθήματος. Σκοπός είναι να παρακολουθούν τα εργαστήρια οι φοιτητές που πραγματικά πιστεύουν ότι έχουν την ανάγκη πρακτικής εξάσκησης και επιπλέον βοήθειας από τους βοηθούς των εργαστηρίων. Δεν υπάρχει κάποια βαθμολογική ενίσχυση για όσους παρακολουθήσουν τα εργαστήρια. Ο στόχος τους είναι καθαρά βοηθητικός ως προς την εξάσκηση στον προγραμματισμό.
Ύλη των εργαστηριακών μαθημάτων (ενδέχεται να τροποποιηθεί):
Εργαστήριο 1: Εισαγωγή στη χρήση του MATLAB/Octave
Εργαστήριο 2: Λογικές πράξεις / Έλεγχος συνθηκών
Εργαστήριο 3: Επαναληπτικές διαδικασίες
Εργαστήριο 4: Συναρτήσεις
Εργαστήριο 5: Διανύσματα
Εργαστήριο 6: Πίνακες
Εργαστήριο 7: Αλγόριθμοι, αναδρομή
Εργαστήριο 8: Μαθηματικές εφαρμογές
MATLAB και συμβατά προγράμματα:
- The Mathworks:
Η επίσημη ιστοσελίδα του MATLAB
- MATLAB (Wikipedia):
Άρθρο στη Wikipedia για το MATLAB, με πολλούς συνδέσμους σε εισαγωγικές και προχωρημένες σημειώσεις, και άλλες πληροφορίες.
http://en.wikipedia.org/wiki/MATLAB
- GNU Octave:
Κλώνος του MATLAB (ανοιχτό λογισμικό)
http://www.gnu.org/software/octave/
- GNU Octave (Wikipedia):
Άρθρο στη Wikipedia για το Octave και συμβατότητά του με το MATLAB
http://en.wikipedia.org/wiki/GNU_Octave
- Octave wiki:
http://wiki.octave.org/Main_Page
- Σημειώσεις MATLAB στο web
ΠΡΟΣΟΧΗ: Οι σημειώσεις αυτές είναι για προχωρημένους και θα είναι χρήσιμες όταν καλυφθεί η βασική ύλη στο μάθημα.
- A practical introduction to MATLAB (M. S. Gockenbach)
- An introduction to MATLAB (D. F. Griffiths)
Youtube videos
- Gates, M. Zuckerberg, C. Bosh campaign for more programmers
https://www.youtube.com/watch?v=nKIu9yen5nc#t=18
Ομιλία Steve Jobs στο Stanford
|
----------------------------------------------------------------------------------------------------------------------------------------------------------
|
|
Εξετάσεις |
-----------------------------------------------------------------------------------------
|
Examinations |
|
Το μάθημα είναι πρώτου εξαμήνου και δεν έχει προαπαιτούμενα |
---------------------------------------------------------------------------------------
|
This course is the first semester and has no prerequisites |
Δρακόπουλος ΜιχάληςΕπίκουρος Καθηγητής Ερευνητικά Ενδιαφέροντα : Υπολογιστική Επιστήμη, Παράλληλη Επεξεργασία, Πεπερασμένα Στοιχεία, Αριθμητική Βελτιστοποίηση. e-mail : mdraco@math.uoa.gr
Προσωπική Ιστοσελίδα: http://users.uoa.gr/~mdraco/ |
----------------------------------------------------------------------------------------------------------------------------------------------------------
|
Michael C. Dracopoulos Dept. of Mathematics, University of Athens Panepistimioupolis, 157 84 Athens, Greece e-mail : mdraco@math.uoa.gr Background
Research Scientific and parallel computing, numerical analysis, finite elements, numerical optimization, simulation and modelling. Publications Teaching
Publications http://users.uoa.gr/~mdraco/publications.html |
|
Προπτυχιακοί φοιτητές του τμήματος Μαθηματικών. |
----------------------------------------------------------------------------------------------
|
Undergraduate students of University of Athens Department of Mathematics |
Βοηθήματα:
- C.F. van Loan & K.-Y.D. Fan. Το MATLAB στην Υπολογιστική Επιστήμη και Τεχνολογία - Μια Εισαγωγή. Εκδόσεις DaVinci, 2012.
- Γ. Γραββάνης & Κ. Γιαννουτάκης. Προγραμματισμός με τη χρήση MATLAB. Εκδόσεις Παπασωτηρίου, 2012.
|
----------------------------------------------------------------------------------------------------------------------------------------------------------
|
Περιεχόμενο μαθήματος. Τι είναι Matlab. Ο ρόλος των υπολογιστών. Αλγόριθμος. Βήματα στην υπολογιστική επίλυση προβλήματος. Βασικές αλγοριθμικές ενέργειες. Αλγόριθμοι και Matlab. Βασικές προγραμματιστικές έννοιες. Περιβάλλον προγραμματισμού (Qtoctave). Αριθμητικές σταθερές. Μεταβλητές. Εκφράσεις. Υπολογισμός εκφράσεων. Εντολές ανάθεσης. Η εικόνα της μνήμης. Έξοδος. Ερωτηματικό, κόμμα, τρεις τελείες. Μορφοποίηση εξόδου. Μετατροπή βαθμών Fahrenheit σε βαθμούς Celsius. m-αρχεία scripts. Ο editor του Qtoctave. Η εντολή input. Έξοδος με fprintf. Παραδείγματα fprintf.
Λέξεις – κλειδιά: Αλγόριθμος, Αριθμητικές σταθερές. Μεταβλητές, Εκφράσεις, Εντολές ανάθεσης, Έξοδος, εντολή input, Έξοδος με fprintf
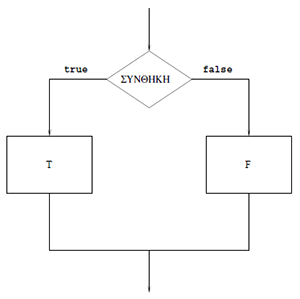
Μερικά χρήσιμα εργαλεία. Ακέραια διαίρεση και υπόλοιπα. Λογικά (boolean) δεδομένα. Λογικές (boolean) εκφράσεις. Λογικές (boolean) εκφράσεις και τελεστές. Σύνθετες λογικές εκφράσεις. Λανθασμένη χρήση των λογικών τελεστών. Κανόνας υπολογισμού λογικών εκφράσεων. Παράδειγμα: εύρεση δίσεκτων ετών. Εντολές ελέγχου και επανάληψης. Εκτέλεση υπό συνθήκη: η εντολή if-else. Εκτέλεση υπό συνθήκη: η εντολή if. Παραδείγματα. Διάταξη 3 αριθμών. Προγραμματιστικά ιδιώματα με λογικές εκφράσεις. Σύνθετα if. Η εντολή While. Δυνάμεις του 2. Άθροισμα ψηφίων ακεραίου. Ατέρμονες επαναλήψεις. Αντιστροφή ψηφίων ακεραίου. Μία άλλη εντολή επανάληψης. Η εντολή for. Παραδείγματα for. Αρμονικοί αριθμοί. Σχέση for και while. While αντί for. Επεξεργασία αγνώστου πλήθους δεδομένων. Άθροισμα θετικών όρων λίστας. For μέσα σε for. Circle.m. Triangle.m. Αριθμοί Fibonacci. Πρώτοι αριθμοί. Αλγόριθμος Π1: Έλεγχος πρώτων αριθμών. Πρόγραμμα για τον αλγόριθμο Π1. Βελτίωση της αποτελεσματικότητας του Π1: Αλγόριθμος Π2. Πρόγραμμα για τον αλγόριθμο Π2. Η εντολή return. Προβλήματα με τον αλγόριθμο Π2. Μέθοδος για τον αλγόριθμο Π3.
Λέξεις – κλειδιά: Else if, if , while
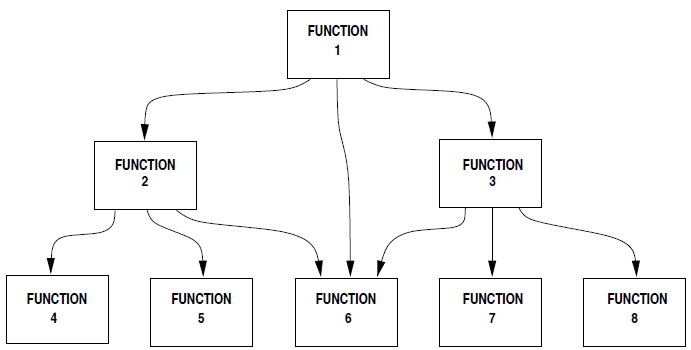
Ροή ελέγχου. Μια άλλη μορφή ροής ελέγχου: Συναρτήσεις. Η μέθοδος Newton για τετραγωνική ρίζα. Τετραγωνική ρίζα με αλγόριθμο Newton. Μια γεωμετρική προσέγγιση. Η μεγάλη ιδέα πίσω από τις συναρτήσεις. Συναρτήσεις. Σχεδιασμός συναρτήσεων, απόκρυψη υλοποίησης. Προγραμματισμός συναρτήσεων. Τοπικές μεταβλητές. Δομή προγραμμάτων: ιεραρχία συναρτήσεων. Ροή ελέγχου συνάρτησης. Συνάρτηση για έλεγχο πρώτων αριθμών Ι. Η εντολή return. Συνάρτηση για έλεγχο πρώτων αριθμών ΙΙ. Ζεύγη πρώτων αριθμών. Υπενθύμιση: διάταξη πρώτων αριθμών. Διάταξη πρώτων αριθμών.
Λέξεις – κλειδιά: Συναρτήσεις, Ροή ελέγχου συνάρτησης, εντολή return
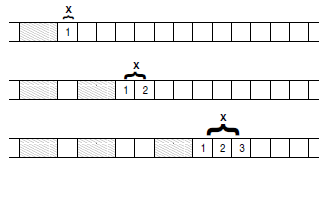Δομές δεδομένων. Μονοδιάστατοι πίνακες (array). Arrays στο Matlab. Ο τελεστής : Άνω κάτω τελεία. Ο μηχανισμός της εντολής for. Είσοδος/έξοδος μονοδιάστατων πινάκων. Sprintf. Επεξεργασία με μονοδιάστατους πίνακες. Μέγιστο και ελάχιστο στοιχείο μονοδιάστατου πίνακα. Παραδείγματα με arrays. Αρχικοποίηση πινάκων. Το κόσκινο του Ερατοσθένη (3ος αιώνας π.χ.). Δισδιάστατοι πίνακες. Ειδική περίπτωση: μονοδιάστατοι πίνακες. Αναθέσεις τιμών σε μεταβλητές πινάκων. Είσοδος/έξοδος δισδιάστατων πινάκων. Επεξεργασία με δισδιάστατους πίνακες. Χρήσιμες συνάρτησες. Συναρτήσεις με παραμέτρους πίνακες. Συναρτήσεις που επιστρέφουν διανύσματα. Συναρτήσεις που επιστρέφουν πίνακες. Γραφικές παραστάσεις: η εντολή plot. Γραφική παράσταση πολυωνύμου. Υπολογισμός τιμών πολυωνύμου. Ο κανόνας του Horner. Υπολογισμός ρητών συναρτήσεων.
Λέξεις – κλειδιά: Μονοδιάστατοι πίνακες , Δισδιάστατοι πίνακες, εντολή plot
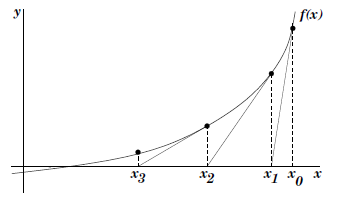
Μέγιστος κοινός διαιρέτης (gcd) – Εξαντλητικός αλγόριθμος Δ1. Παρατηρήσεις στον αλγόριθμο Δ1. Μέγιστος κοινός διαιρέτης (gcd) – Αλγόριθμος του Ευκλείδη Δ2. Αριθμητικοί αλγόριθμοι. Διαδοχικές προσεγγίσεις. Έλεγχος “ισότητας” δύο πραγματικών αριθμών. Η μέθοδος Newton για τετραγωνική ρίζα. Τετραγωνική ρίζα με αλγόριθμο Newton. Ανάπτυγμα σειράς. Ο υπολογισμός της s = Σ 1/2i. Το πρόγραμμα για τη σειρά του Ζήνωνα. Υπολογισμός τετραγωνικής ρίζας – Σειρά Taylor. Προγραμματισμός της μεθόδου Taylor για √x. Τετραγωνική ρίζα με αλγόριθμο Taylor – Ι. Όρια σύγκλησης σειράς Taylor. Τετραγωνική ρίζα με αλγόριθμο Taylor – ΙΙ. Προσομοίωση (simulation). Ανάλυση συμπεράσματα.
Λέξεις – κλειδιά: Μέγιστος κοινός διαιρέτης , Η μέθοδος Newton για τετραγωνική ρίζα, Σειρά Taylor
Αποτελεσματικότητα αλγορίθμων. Μέτρηση της αποτελεσματικότητας. Πολυπλοκότητα αλγορίθμου Ο. Ανάλυση παραγόντων. Κανονικοποιημένες μονάδες χρόνου. Αναλυτική μέτρηση πράξεων. Μέτρηση πράξεων για διάφορα n. Πυθαγόρειες τριάδες. Πυθαγόρειες τριάδες αλγόριθμος 1. Παρατηρήσεις στον αλγόριθμο 1. Πυθαγόρειες τριάδες αλγόριθμος 2. Παρατηρήσεις στον αλγόριθμο 2. Πυθαγόρειες τριάδες αλγόριθμος 3.
Λέξεις – κλειδιά: Αποτελεσματικότητα αλγορίθμων, Πολυπλοκότητα αλγορίθμου Ο, Πυθαγόρειες τριάδες
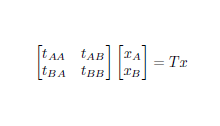Ο συμβολισμός μεγάλο Ο. Εσωτερικό γινόμενο. Πολλαπλασιασμός πίνακα με διάνυσμα. Παράδειγμα πολλαπλασιασμού πίνακα με διάνυσμα. Γινόμενο πινάκων. Παράδειγμα γινόμενου πινάκων.
Λέξεις – κλειδιά: Εσωτερικό γινόμενο, Γινόμενο πινάκων
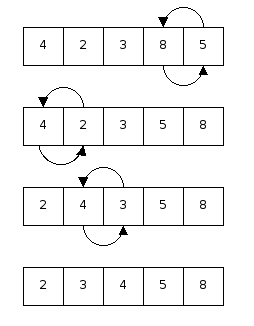
Αναζήτηση (search). Αλγόριθμος γραμμικής αναζήτησης. Δυαδική binary αναζήτηση. Αλγόριθμος δυαδικής αναζήτησης. Ταξινόμηση (sort). Ταξινόμηση με επιλογή (selection). Αλγόριθμος selection sort. Ταξινόμηση με εναλλαγή (exchange). Ο αλγόριθμος της φυσαλίδας (bubble sort) - I. Πρόβλημα με τον αλγόριθμο Ι. Ο αλγόριθμος της φυσαλίδας (bubble sort) - IΙ. Ανάλυση του αλγορίθμου ΙΙ. Ταξινόμηση με εισαγωγή (insertion). Αλγόριθμος insertion sort. Ανάλυση αλγορίθμου εισαγωγής.
Λέξεις – κλειδιά: Αναζήτηση, γραμμική αναζήτηση, Δυαδική binary αναζήτηση, Ταξινόμηση, αλγόριθμος της φυσαλίδας
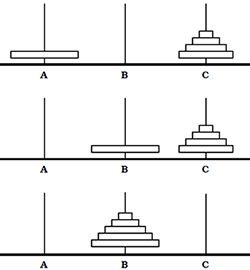
Αναδρομικές μέθοδοι. Αναδρομικός αλγόριθμος n!. Αναδρομικός αλγόριθμος του Ευκλείδη. Οι πύργοι του Hanoi. Οι πύργοι του Hanoi (Αναδρομική λύση). Αλγόριθμος για πύργους Hanoi. Αναδρομική μέθοδος για πύργους Hanoi. Αλφαριθμητικά δεδομένα (strings). Ο θρύλος των πύργων Hanoi. Προβλήματα με αναδρομή.
Λέξεις – κλειδιά: Αναδρομικός αλγόριθμος, Οι πύργοι του Hanoi
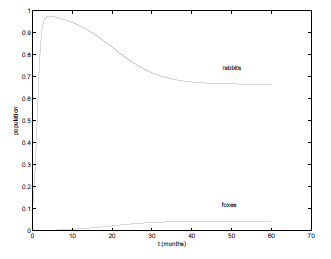
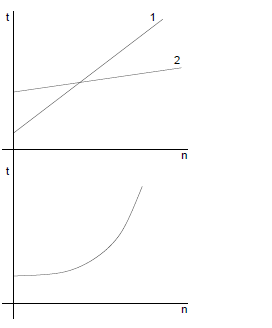
Προσομοίωση. Δομή αλγορίθμων προσομοίωσης. Παράδειγμα επένδυσης. Επένδυση. Παράδειγμα καταδίωξης. Καταδίωξη. Αλγόριθμος καταδίωξης. Η πορεία του ταύρου. Η απόσταση ταύρου πεζοπόρου. Παράδειγμα δυναμικής. Δυναμική. Αλγόριθμος αναπήδησης. Γραφική παράσταση αναπήδησης. Δυναμική πληθυσμών. Πληθυσμός με περιορισμένα αποθέματα τροφής. Αλγόριθμος για θεμελιώδη εξ. Οικολογίας. Αρπακτικά και λεία. Αλγόριθμος αρπακτικών και λείας.
Λέξεις – κλειδιά: Προσομοίωση, Επένδυση, Καταδίωξη, Δυναμική, Αναπήδηση, Αρπακτικά και λεία
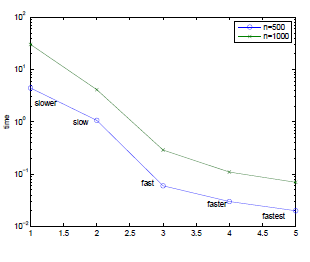
MATLAB (MATrix LABoratory). Χαρακτηριστικά του Matlab. Βοήθεια στο Μatlab. Τα πάντα είναι πίνακες. Εισαγωγή πινάκων. Πράξεις πινάκων. Εντολές, εκφράσεις, Μεταβλητές. Κατασκευή πινάκων. Παρατηρήσεις, παραδείγματα. Υποπίνακες. Η εντολή for. Η εντολή while. Η εντολή if. Λογικές σχέσεις και τελεστές. Βαθμωτές συναρτήσεις. Διανυσματικές συναρτήσεις. Συναρτήσεις πινάκων. m-αρχεία. Γραφικά – οι συναρτήσεις plot και semilogy. Χρήσιμες συναρτήσεις. Δημιουργία τριδιαγώνιου πίνακα. Αποτελεσματικότητα συναρτήσεων. Χρόνοι εκτέλεσης σε Pentium 4. Οδηγίες για γρηγορότερα προγράμματα MATLAB.
Λέξεις – κλειδιά: Κατασκευή πινάκων, Υποπίνακες, Λογικές σχέσεις και τελεστές, Συναρτήσεις πινάκων, m-αρχεία, plot, semilogy
- Εισαγωγή
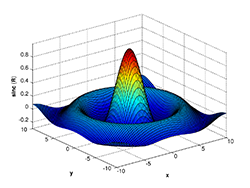
- Έλεγχος συνθηκών
- Δομές επανάληψης
- Συναρτήσεις
- Πίνακες [1/2] (Διανύσματα)
- Πίνακες [2/2] (Δισδιάστατοι)
- Αναδρομή
- Συστήματα αρίθμησης
Ανοικτό Ακαδ. Μάθημα
Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -
