Βασική Άλγεβρα
Ευάγγελος Ράπτης
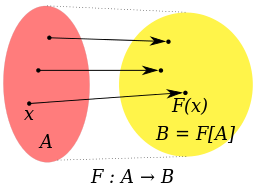
Σκοπός του μαθήματος είναι να βοηθήσει στην κατανόηση της οργάνωσης των συνόλων. Η οργάνωση αυτή, από την πλευρά της Άλγεβρας, επιτυγχάνεται με τη μελέτη των πράξεων. Κυρίως μελετώνται δύο τύποι οργανώσεων, οι Δακτύλιοι και οι Ομάδες. Γενικά οι οργανώσεις αυτές λέγονται Δομές.Σημαντική επίσης είναι και η έννοια του ισομορφισμού δομών, όπου δύο δομές ως σύνολα είναι διαφορετικές, αλλά στην πραγματικότητα είναι ίδιες
ΛιγότεραΣκοπός του μαθήματος είναι να βοηθήσει στην κατανόηση της οργάνωσης των συνόλων. Η οργάνωση αυτή, από την πλευρά της Άλγεβρας, επιτυγχάνεται με τη μελέτη των πράξεων. Κυρίως μελετώνται δύο τύποι οργανώσεων, οι Δακτύλιοι και οι Ομάδες. Γενικά οι οργανώσεις αυτές λέγονται Δομές.Σημαντική επίσης είναι και η έννοια του ισομορφισμού δομών, όπου δύο δομές ως σύνολα είναι διαφορετικές, αλλά στην πραγματικότητα είναι ίδιες
Σκοπός του μαθήματος είναι να βοηθήσει στην κατανόηση της οργάνωσης των συνόλων. Η οργάνωση αυτή, από την πλευρά της Άλγεβρας, επιτυγχάνεται με τη μελέτη των πράξεων. Κυρίως μελετώνται δύο τύποι οργανώσεων, οι Δακτύλιοι και οι Ομάδες. Γενικά οι οργανώσεις αυτές λέγονται Δομές.Σημαντική επίσης είναι και η έννοια του ισομορφισμού δομών, όπου δύο δομές ως σύνολα είναι διαφορετικές, αλλά στην πραγματικότητα είναι ίδιες
Περίγραμμα
Περιεχόμενο μαθήματος
Ύλη (και ενδεικτικό χρονοδιάγραμμα σε εβδομάδες)
1. Διαιρετότητα στους ακέραιους (Ευκλείδεια διαίρεση, μκδ, Θεμελιώδες Θεώρημα της Αριθμητικής, ισοτιμίες) (1)
2. Ακέραιοι modulo n (πράξεις, αντιστρέψιμα στοιχεία, Θεώρημα του Euler) (1)
3. Δακτύλιοι (ορισμοί, παραδείγματα, βασικές ιδιότητες) (1)
4. Πολυώνυμα (διαιρετότητα, ρίζες) (2-)
5. Ομομορφισμοί και Ιδεώδη (ορισμοί, παραδείγματα, δακτύλιος πηλίκο) (2-)
6. Ομάδες (ομάδες συμμετρίας, συμμετρικές ομάδες, βασικές ιδιότητες, τάξη) (2)
7. Υποομάδες, Θεώρημα του Lagrange, Κυκλικές ομάδες (1)
8. Ομομορφισμοί (ορισμοί, παραδείγματα) (1-)
9. Κανονικές υποομάδες, Ομάδες πηλίκα (1)
Μαθησιακοί στόχοι
Σκοπός του μαθήματος είναι να βοηθήσει στην κατανόηση της οργάνωσης των συνόλων. Η οργάνωση αυτή, από την πλευρά της Άλγεβρας, επιτυγχάνεται με τη μελέτη των πράξεων. Κυρίως μελετώνται δύο τύποι οργανώσεων, οι Δακτύλιοι και οι Ομάδες. Γενικά οι οργανώσεις αυτές λέγονται Δομές.Σημαντική επίσης είναι και η έννοια του ισομορφισμού δομών, όπου δύο δομές ως σύνολα είναι διαφορετικές, αλλά στην πραγματικότητα είναι ίδιες.
Μέθοδοι διδασκαλίας
Διδασκαλία καθ΄ έδρας – Ασκήσεις
Βιβλιογραφία
Ράπτης Ευάγγελος, Βασική άλγεβρα (421) (Χειμερινό εξάμηνο 2014-15)
Προαπαιτούμενα
- Γραμμική Άλγεβρα Ι
- Γραμμική Άλγεβρα ΙΙ
Ομάδα στόχος
Προπτυχιακοί φοιτητές Τμημάτων Μαθηματικών, Πληροφορικής και Πολυτεχνικών Σχολών
Ύλη (και ενδεικτικό χρονοδιάγραμμα σε εβδομάδες)
1. Διαιρετότητα στους ακέραιους (Ευκλείδεια διαίρεση, μκδ, Θεμελιώδες Θεώρημα της Αριθμητικής, ισοτιμίες) (1)
2. Ακέραιοι modulo n (πράξεις, αντιστρέψιμα στοιχεία, Θεώρημα του Euler) (1)
3. Δακτύλιοι (ορισμοί, παραδείγματα, βασικές ιδιότητες) (1)
4. Πολυώνυμα (διαιρετότητα, ρίζες) (2-)
5. Ομομορφισμοί και Ιδεώδη (ορισμοί, παραδείγματα, δακτύλιος πηλίκο) (2-)
6. Ομάδες (ομάδες συμμετρίας, συμμετρικές ομάδες, βασικές ιδιότητες, τάξη) (2)
7. Υποομάδες, Θεώρημα του Lagrange, Κυκλικές ομάδες (1)
8. Ομομορφισμοί (ορισμοί, παραδείγματα) (1-)
9. Κανονικές υποομάδες, Ομάδες πηλίκα (1)
Σκοπός του μαθήματος είναι να βοηθήσει στην κατανόηση της οργάνωσης των συνόλων. Η οργάνωση αυτή, από την πλευρά της Άλγεβρας, επιτυγχάνεται με τη μελέτη των πράξεων. Κυρίως μελετώνται δύο τύποι οργανώσεων, οι Δακτύλιοι και οι Ομάδες. Γενικά οι οργανώσεις αυτές λέγονται Δομές.Σημαντική επίσης είναι και η έννοια του ισομορφισμού δομών, όπου δύο δομές ως σύνολα είναι διαφορετικές, αλλά στην πραγματικότητα είναι ίδιες.
Διδασκαλία καθ΄ έδρας – Ασκήσεις
Ράπτης Ευάγγελος, Βασική άλγεβρα (421) (Χειμερινό εξάμηνο 2014-15)
- Γραμμική Άλγεβρα Ι
- Γραμμική Άλγεβρα ΙΙ
Προπτυχιακοί φοιτητές Τμημάτων Μαθηματικών, Πληροφορικής και Πολυτεχνικών Σχολών
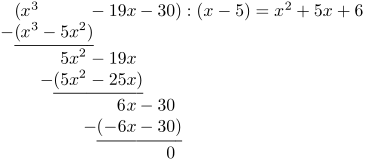Ευκλείδεια διαίρεση, μκδ, Θεμελιώδες Θεώρημα της Αριθμητικής, ισοτιμίες.
Πράξεις με ακέραιους modulo n, αντιστρέψιμα στοιχεία, Θεώρημα του Euler.
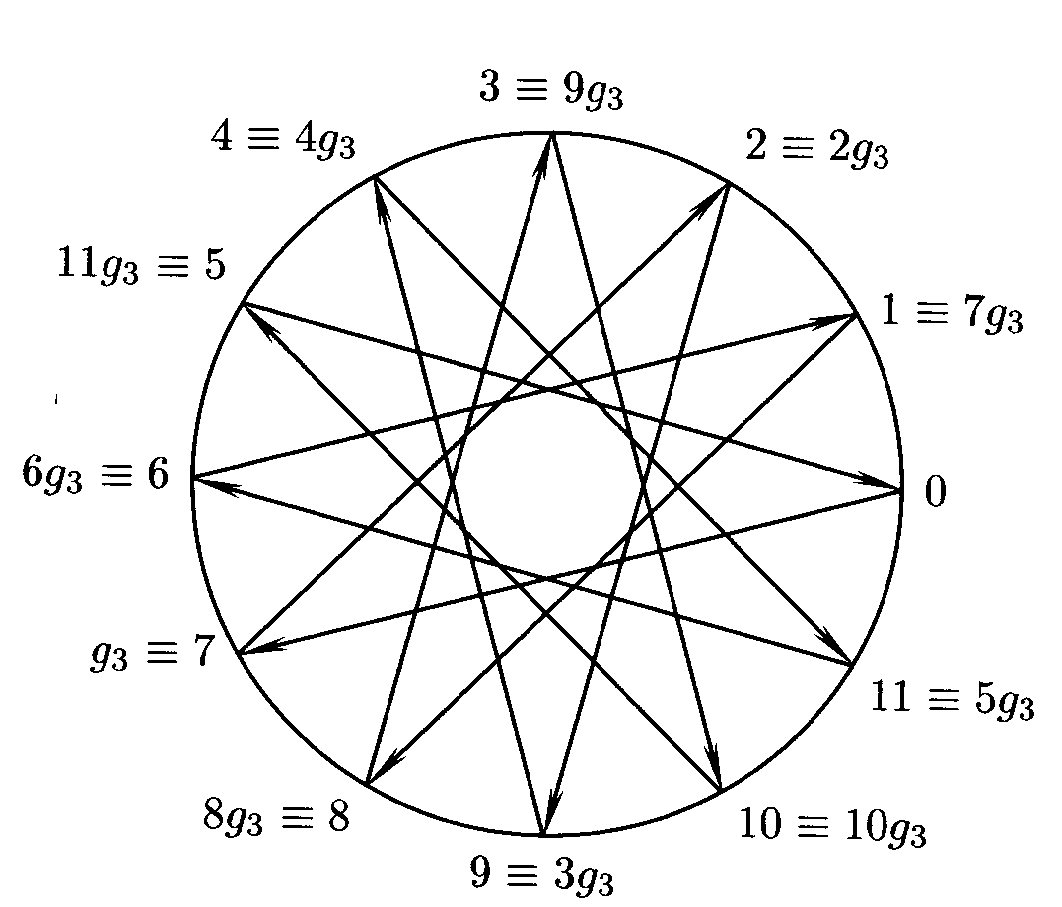
Στο κεφάλαιο αυτό θα μελετήσουμε τους ορισμούς και τις βασικές ιδιότητες των Δακτυλίων καθώς και Παραδειγματά τους.
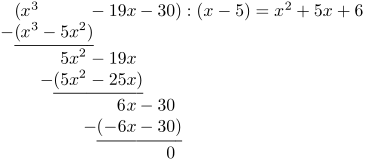Ορισμός, διαιρετότητα, ρίζες, Θεώρημα πρώτων αριθμών
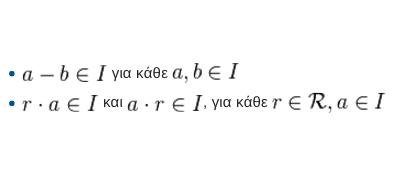Ορισμοί και παραδείγματα ομοιμορφίσμου.
Ορισμός Ιδεώδους, Ιδιότητες, Ασκήσεις και Παραδείγματα στα Ιδεώδη.
Ορισμός Συμπλόκου ή πλευρικής κλάσης Ιδεώδους.
Ορισμός Δακτύλιο-Πηλίκο, Παραδείγματα και Ασκήσεις.
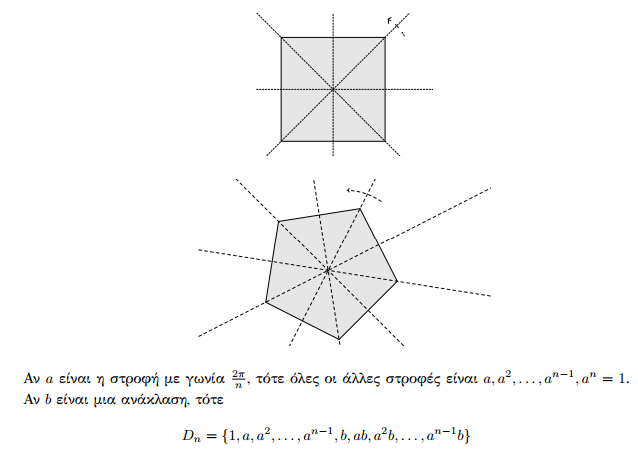Ομάδες συμμετρίας, συμμετρικές ομάδες, βασικές ιδιότητες, τάξη ομάδας
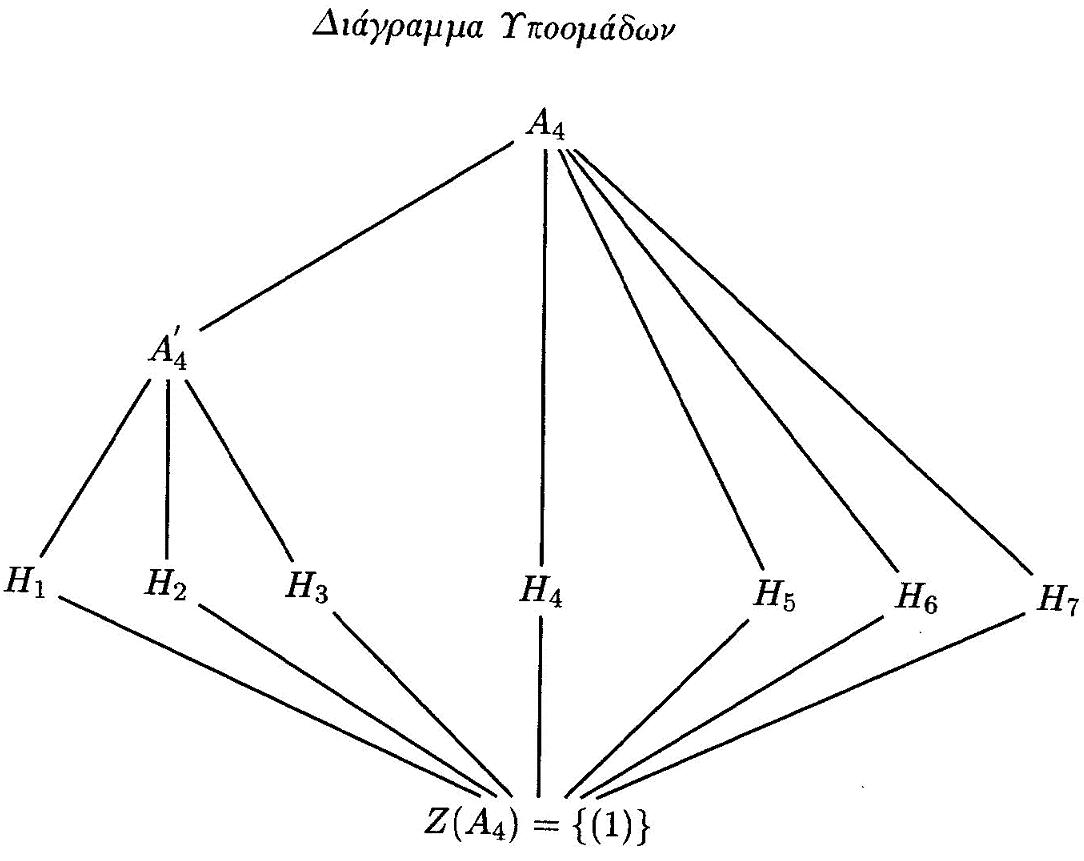Ισομορφισμός Ομάδων, Τάξη Ομάδων, Θεώρημα Lagrange και η αποδειξή του, Ομάδα Klein.
Ορισμοί - άρτιες, περιττές μετάθεσεις, Ασκήσεις.
Ομάδες Μεταθέσεων, Αντιμεταθέσεις(Ορισμός, Ιδιότητες, Παραδείγματα)
Ορισμός Κανονικής Υπομάδας, Ομάδες μεταθέσεων( ή συμμετρικές ομάδες),Ομάδες Πηλίκα.
Ορισμοί, Ιδιότητες, Παραδείγματα και Ασκήσεις
Αυτό το κεφάλαιο περιέχει λύσεις παλαιών θεμάτων εξετάσεων από το 2003 έως το 2014.
Ανοικτό Ακαδ. Μάθημα
Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -
