Υπολογιστική Γεωμετρία
Ιωάννης Εμίρης
Eισαγωγή στους Γεωμετρικούς Αλγόριθμους και προεκτάσεις προς τις ερευνητικά ενεργές περιοχές της Υπολογιστικής Γεωμετρίας. Η ύλη μεταβάλλεται κάθε χρόνο, σε κάποιο βαθμό.
Kυρτότητα: Κυρτό περίβλημα (convex hull) σε 2 και 3 διαστάσεις, αυξητικός αλγόριθμος, αλγόριθμος περιτύλιξης και πολυπλοκότητα ευαίσθητη εξόδου (output sensitive), μέθοδος Διαίρει και βασίλευε. Άθροισμα Minkowski πολυέδρων. Γραμμική βελτιστοποίηση (ή γραμμικός προγραμματισμός), δυϊσμός, τυχαιότητα. Ζητήματα υλοποίησης, εκφυλισμένα δεδομένα και διαταραχή.
Τριγωνοποιήσεις: Διάγραμμα Voronoi και κατασκευή ως προβολή πολυέδρου, τριγωνοποίηση Delaunay και δυϊσμός με το Διάγραμμα Voronoi, εφαρμογές στη δομική μοριακή βιολογία, στην κίνηση ρομπότ ανάμεσα σε εμπόδια, και την κατασκευή πλέγματος (mesh). Προβλήματα ορατότητας, φύλαξη μουσείου (art gallery), τριγωνοποίηση σε 2 διαστάσεις, μέθοδος σάρωσης.
Γεωμετρική αναζήτηση: Δομές γεωμετρικών δεδομένων, αναζήτηση περιοχής (range search) σε 2 και περισσότερες διαστάσεις, (προσεγγιστική) εύρεση πλησιέστερου γείτονα με δενδρικές δομές ή πίνακες κατακερματισμού, εφαρμογές σε Εξόρυξη δεδομένων και Γεωγραφικά Συστήματα πληροφόρησης (GIS).
(Αν επιτρέψει ο χρόνος: Διατάξεις ευθυγράμμων τμημάτων και ευθειών στο επίπεδο.)
Υλοποιήσεις σε Python και CGAL/C++.
Eισαγωγή στους Γεωμετρικούς Αλγόριθμους και προεκτάσεις προς τις ερευνητικά ενεργές περιοχές της Υπολογιστικής Γεωμετρίας. Η ύλη μεταβάλλεται κάθε χρόνο, σε κάποιο βαθμό.
Kυρτότητα: Κυρτό περίβλημα (convex hull) σε 2 και 3 διαστάσεις, αυξητικός αλγόριθμος, αλγόριθμος περιτύλιξης και πολυπλοκότητα ευαίσθητη εξόδου (output sensitive), μέθοδος Διαίρει και βασίλευε. Άθροισμα Minkowski πολυέδρων. Γραμμική βελτιστοποίηση (ή γραμμικός προγραμματισμός), δυϊσμός, τυχαιότητα. Ζητήματα υλοποίησης, εκφυλισμένα δεδομένα και διαταραχή.
Τριγωνοποιήσεις: Διάγραμμα Voronoi και κατασκευή ως προβολή πολυέδρου, τριγωνοποίηση Delaunay και δυϊσμός με το Διάγραμμα Voronoi, εφαρμογές στη δομική μοριακή βιολογία, στην κίνηση ρομπότ ανάμεσα σε εμπόδια, και την κατασκευή πλέγματος (mesh). Προβλήματα ορατότητας, φύλαξη μουσείου (art gallery), τριγωνοποίηση σε 2 διαστάσεις, μέθοδος σάρωσης.
Γεωμετρική αναζήτηση: Δομές γεωμετρικών δεδομένων, αναζήτηση περιοχής (range search) σε 2 και περισσότερες διαστάσεις, (προσεγγι
Eισαγωγή στους Γεωμετρικούς Αλγόριθμους και προεκτάσεις προς τις ερευνητικά ενεργές περιοχές της Υπολογιστικής Γεωμετρίας. Η ύλη μεταβάλλεται κάθε χρόνο, σε κάποιο βαθμό.
Kυρτότητα: Κυρτό περίβλημα (convex hull) σε 2 και 3 διαστάσεις, αυξητικός αλγόριθμος, αλγόριθμος περιτύλιξης και πολυπλοκότητα ευαίσθητη εξόδου (output sensitive), μέθοδος Διαίρει και βασίλευε. Άθροισμα Minkowski πολυέδρων. Γραμμική βελτιστοποίηση (ή γραμμικός προγραμματισμός), δυϊσμός, τυχαιότητα. Ζητήματα υλοποίησης, εκφυλισμένα δεδομένα και διαταραχή.
Τριγωνοποιήσεις: Διάγραμμα Voronoi και κατασκευή ως προβολή πολυέδρου, τριγωνοποίηση Delaunay και δυϊσμός με το Διάγραμμα Voronoi, εφαρμογές στη δομική μοριακή βιολογία, στην κίνηση ρομπότ ανάμεσα σε εμπόδια, και την κατασκευή πλέγματος (mesh). Προβλήματα ορατότητας, φύλαξη μουσείου (art gallery), τριγωνοποίηση σε 2 διαστάσεις, μέθοδος σάρωσης.
Γεωμετρική αναζήτηση: Δομές γεωμετρικών δεδομένων, αναζήτηση περιοχής (range search) σε 2 και περισσότερες διαστάσεις, (προσεγγι
Περίγραμμα

Περιεχόμενο μαθήματος
Στο εαρινό εξάμηνο 2015, θα εστιάσουμε στα εξής θέματα (που συνδέονται με τα ερευνητικά ενδιαφέροντα της Εργαστηρίου Γεωμετρικών & Αλγεβρικών Αλγορίθμων):
Κυρτότητα: Κυρτά πολύγωνα και πολύεδρα σε 2, 3 και γενικές διαστάσεις, κατασκευή κυρτού περιβλήματος. Επέκταση στον γραμμικό προγραμματισμό. Δυϊσμός. Ορατότητα σε πολυγωνικά περιβάλλοντα. Χρήση κυρτών πολυέδρων για την τριγωνοποίηση Delaunay, διαγράμματα Voronoi. Δομές γεωμετρικών δεδομένων και Γεωμετρική αναζήτηση, (προσεγγιστική) εύρεση πλησιέστερου γείτονα, εξόρυξη δεδομένων. Yλοποίηση γεωμετρικών αλγορίθμων με Python και χρήση της C++ βιβλιοθήκης CGAL (Πληροφορίες).
Διδάσκοντες
Εμίρης Ιωάννης
Θέση: Καθηγητής
Τομέας: Θεωρητική Πληροφορική
Tμήμα Πληροφορικής & Τηλεπικοινωνιών
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
Προτεινόμενα συγγράμματα
Γιάννης Εμίρης. Υπολογιστική γεωμετρία: μία σύγχρονη αλγοριθμική προσέγγιση. Κλειδάριθμος, 2008.
Mark Overmars et al. Computational geometry and Applications. Springer. Μετάφραση: Πανεπιστημιακές εκδόσεις Κρήτης, 2011.
Περαιτέρω βοηθήματα: http://cgi.di.uoa.gr/~compgeom/2012/biblio.html
Ομάδα στόχος
Προπτυχιακοί φοιτητές του τμήματος Πληροφορικής και Τηλεπικοινωνιών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Προαπαιτούμενα
Δομές Δεδομένων και Τεχν. Προγραμματισμού
Σημειώματα Δικαιωμάτων Πνευματικής Ιδιοκτησίας
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Ιωάννης Εμίρης. Υπολογιστική Γεωμετρία. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/DI113/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».
[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
Στο εαρινό εξάμηνο 2015, θα εστιάσουμε στα εξής θέματα (που συνδέονται με τα ερευνητικά ενδιαφέροντα της Εργαστηρίου Γεωμετρικών & Αλγεβρικών Αλγορίθμων):
Κυρτότητα: Κυρτά πολύγωνα και πολύεδρα σε 2, 3 και γενικές διαστάσεις, κατασκευή κυρτού περιβλήματος. Επέκταση στον γραμμικό προγραμματισμό. Δυϊσμός. Ορατότητα σε πολυγωνικά περιβάλλοντα. Χρήση κυρτών πολυέδρων για την τριγωνοποίηση Delaunay, διαγράμματα Voronoi. Δομές γεωμετρικών δεδομένων και Γεωμετρική αναζήτηση, (προσεγγιστική) εύρεση πλησιέστερου γείτονα, εξόρυξη δεδομένων. Yλοποίηση γεωμετρικών αλγορίθμων με Python και χρήση της C++ βιβλιοθήκης CGAL (Πληροφορίες).
Εμίρης Ιωάννης
Θέση: Καθηγητής
Τομέας: Θεωρητική Πληροφορική
Tμήμα Πληροφορικής & Τηλεπικοινωνιών
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών
Γιάννης Εμίρης. Υπολογιστική γεωμετρία: μία σύγχρονη αλγοριθμική προσέγγιση. Κλειδάριθμος, 2008.
Mark Overmars et al. Computational geometry and Applications. Springer. Μετάφραση: Πανεπιστημιακές εκδόσεις Κρήτης, 2011.
Περαιτέρω βοηθήματα: http://cgi.di.uoa.gr/~compgeom/2012/biblio.html
Προπτυχιακοί φοιτητές του τμήματος Πληροφορικής και Τηλεπικοινωνιών του Εθνικού και Καποδιστριακού Πανεπιστημίου Αθηνών.
Δομές Δεδομένων και Τεχν. Προγραμματισμού
Για το υλικό του παρόντος μαθήματος ισχύουν τα ακόλουθα σημειώματα.
Σημείωμα Ιστορικού Εκδόσεων Έργου
Το παρόν έργο αποτελεί την έκδοση 1.0.
Έχουν προηγηθεί οι κάτωθι εκδόσεις:
- Έκδοση διαθέσιμη εδώ.
Σημείωμα Αναφοράς
Copyright Εθνικόν και Καποδιστριακόν Πανεπιστήμιον Αθηνών, Ιωάννης Εμίρης. Υπολογιστική Γεωμετρία. Έκδοση: 1.0. Αθήνα 2015. Διαθέσιμο από τη δικτυακή διεύθυνση: http://opencourses.uoa.gr/courses/DI113/.
Σημείωμα Αδειοδότησης
Το παρόν υλικό διατίθεται με τους όρους της άδειας χρήσης Creative Commons Αναφορά, Μη Εμπορική Χρήση Παρόμοια Διανομή 4.0 [1] ή μεταγενέστερη, Διεθνής Έκδοση. Εξαιρούνται τα αυτοτελή έργα τρίτων π.χ. φωτογραφίες, διαγράμματα κ.λ.π., τα οποία εμπεριέχονται σε αυτό και τα οποία αναφέρονται μαζί με τους όρους χρήσης τους στο «Σημείωμα Χρήσης Έργων Τρίτων».

[1] http://creativecommons.org/licenses/by-nc-sa/4.0/
Ως Μη Εμπορική ορίζεται η χρήση:
- που δεν περιλαμβάνει άμεσο ή έμμεσο οικονομικό όφελος από την χρήση του έργου, για το διανομέα του έργου και αδειοδόχο
- που δεν περιλαμβάνει οικονομική συναλλαγή ως προϋπόθεση για τη χρήση ή πρόσβαση στο έργο
- που δεν προσπορίζει στο διανομέα του έργου και αδειοδόχο έμμεσο οικονομικό όφελος (π.χ. διαφημίσεις) από την προβολή του έργου σε διαδικτυακό τόπο
Ο δικαιούχος μπορεί να παρέχει στον αδειοδόχο ξεχωριστή άδεια να χρησιμοποιεί το έργο για εμπορική χρήση, εφόσον αυτό του ζητηθεί.
Διατήρηση Σημειωμάτων
- Οποιαδήποτε αναπαραγωγή ή διασκευή του υλικού θα πρέπει να συμπεριλαμβάνει:
- το Σημείωμα Αναφοράς
- το Σημείωμα Αδειοδότησης
- τη δήλωση Διατήρησης Σημειωμάτων
- το Σημείωμα Χρήσης Έργων Τρίτων (εφόσον υπάρχει)
μαζί με τους συνοδευόμενους υπερσυνδέσμους.
- Τι είναι η Γεωμετρία;
- Που είναι η Γεωμετρία;
- Τι είναι η Υπολογιστική Γεωμετρία;
Λέξεις Κλειδιά: γεωμετρία, υπολογιστική γεωμετρία
- Κυρτό Περίβλημα σε δύο και τρεις διαστάσεις
- Αυξητικός αλγόριθμος
- Αλγόριθμος περιτύλιξης και πολυπλοκότητα ευαίσθητη εξόδου (output sensitive)
- Μέθοδος Διαίρει και βασίλευε
- Άθροισμα Minkowski πολυέδρων
- Γραμμική βελτιστοποίηση (ή γραμμικός προγραμματισμός)
- Δυϊσμός
Λέξεις Κλειδιά: κυρτό περίβλημα, αυξητικός αλγόριθμος, αλγόριθμος περιτύλιξης, γραμμική βελτιστοποίηση, δυϊσμός
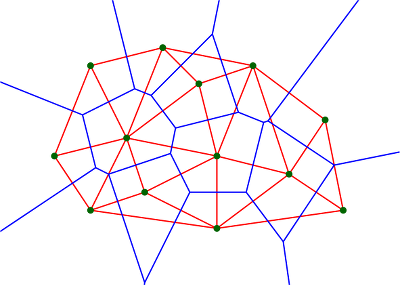
- Διάγραμμα Voronoi
- Τριγωνοποίηση Delaunay
- Αλγόριθμοι και Πολυπλοκότητα
- Αλγόριθμοι Voronoi
- Γενικεύσεις και Αναπαραστάσεις
Λέξεις Κλειδιά: διάγραμμα Voronoi, τριγωνοποίηση Delaunay, αλγόριθμοι Voronoi
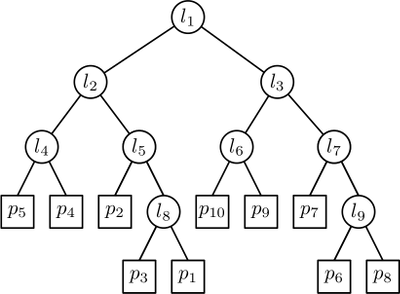
- Δομές γεωμετρικών δεδομένων
- Αναζήτηση περιοχής (range search) σε 2 και περισσότερες διαστάσεις
- Εύρεση πλησιέστερου γείτονα με δενδρικές δομές ή πίνακες κατακερματισμού
- Εφαρμογές σε Εξόρυξη δεδομένων και Γεωγραφικά Συστήματα πληροφόρησης (GIS)
Λέξεις Κλειδιά: δομές γεωμετρικών δεδομένων, αναζήτηση περιοχής σε δύο και περισσότερες διαστάσεις, εύρεση πλησιέστερου γείτονα, δενδρικές δομές, πίνακες κατακερματισμού
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -

