Ανάλυση II

• Ο διανυσματικός χώρος Rⁿ: Ορισμός, Βάση, Διάσταση.
• Εσωτερικό γινόμενο στον Rⁿ: Ορισμός, Ιδιότητες, Γωνία μεταξύ διανυσμάτων, Κάθετα διανύσματα, Διανυσματικές προβολές.
• Εξωτερικό γινόμενο στον R³: Ορισμός, Ιδιότητες, Εμβαδόν παραλληλογράμμου.
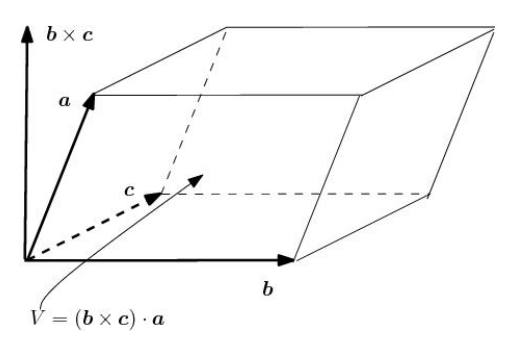
• Μεικτό γινόμενο στον R³: Ορισμός, Όγκος παραλληλεπιπέδου.

Λέξεις Κλειδιά: χώρος Rⁿ, γραμμικός χώρος, ευκλείδεια νόρμα, διανυσματικός χώρος, εσωτερικό γινόμενο, εξωτερικό γινόμενο, μεικτό γινόμενο, κάθετα διανύσματα, διανυσματικές προβολές, εμβαδόν παραλληλογράμμου, όγκος παραλληλεπιπέδου, γεωμετρική ερμηνεία

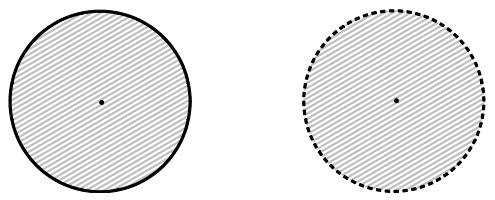
Τοπολογία στον Rⁿ:

• Ανοικτές, Κλειστές σφαίρες. Ανοικτά, κλειστά σύνολα. Σύνορο συνόλου.
• Φραγμένα σύνολα, Συμπαγή σύνολα.

Λέξεις Κλειδιά: ανοικτές σφαίρες, κλειστές σφαίρες, ανοικτά σύνολα, κλειστά σύνολα, σύνορο συνόλου, φραγμένα σύνολα, συμπαγή σύνολα

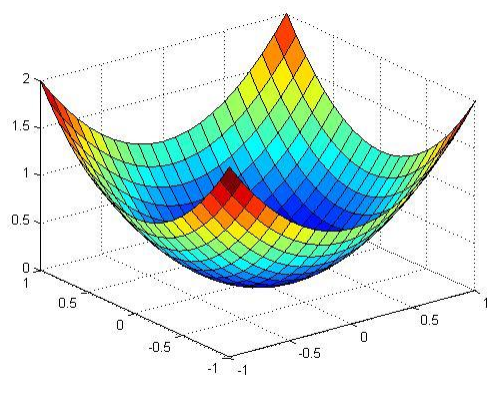
• Καμπύλες, Επιφάνειες (Γενικά). 
• Ευθείες, Επίπεδα στον R³.
• Κυλινδρικές επιφάνειες.
• Επιφάνειες 2^ου βαθμού (τετραγωνικές).

Λέξεις Κλειδιά: καμπύλη, παραμετρικοποιημένη καμπύλη, αναλυτική εξίσωση, καρτεσιανή εξίσωση, παραμετρικές εξισώσεις, καμπύλες Peano, ευθείες στον Rⁿ, επίπεδα στον R³, κυλινδρικές επιφάνειες, επιφάνειες εκ περιστροφής, επίπεδα στον R³, επιφάνειες 2^ου βαθμού στον R³, τετραγωνικές, ελλειψοειδές, μονόχωνο υπερβολοειδές, δίχωνο υπερβολοειδές, ελλειπτικό παραβολοειδές, υπερβολικό παραβολοειδές, ελλειπτικός κώνος

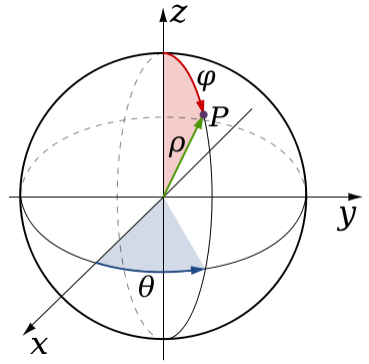
• Καρτεσιανές συντεταγμένες στους R², R³
• Πολικές συντεταγμένες στον R²
• Κυλινδρικές, Σφαιρικές συντεταγμένες στον R³

Λέξεις Κλειδιά: καρτεσιανές συντεταγμένες στον R², καρτεσιανές καμπύλες, πολικές συντεταγμένες στον R², πολικός μετασχηματισμός, πολικές καμπύλες, καρτεσιανές συντεταγμένες στον R³, καρτεσιανές επιφάνειες, κυλινδρικές συντεταγμένες στον R³, κυλινδρικός μετασχηματισμός, κυλινδρικές επιφάνειες, σφαιρικές συντεταγμένες στον R³, σφαιρικός μετασχηματισμός, σφαιρικές επιφάνειες

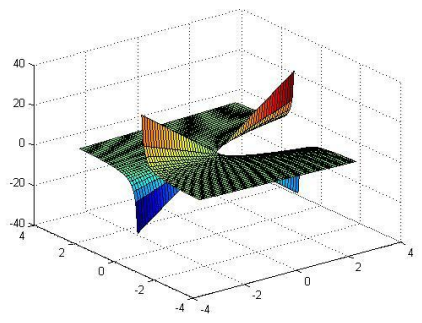
• Συναρτήσεις μεταξύ Ευκλειδείων χώρων: Όρια και συνέχεια.

Λέξεις Κλειδιά: πολυωνυμικές συναρτήσεις, ρητές συναρτήσεις, τριγωνομετρικές συναρτήσεις, εκθετικές συναρτήσεις, λογαριθμικές συναρτήσεις, συναρτήσεις μέσω ολοκληρωμάτων, συναρτήσεις μέσω ορίων, τύπου Weirstrass, τύπου Mandelbrot, συνάρτηση του Riemann, όρια, συνέχεια

• Παράγωγος διανυσματικής συνάρτησης μιας μεταβλητής: Ορισμός, Ταχύτης, Επιτάχυνση.

Λέξεις Κλειδιά: διανυσματική θέση, ταχύτητα, επιτάχυνση

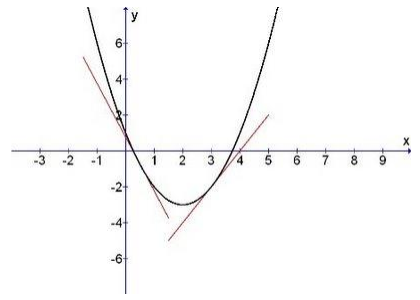
• Μερικές παράγωγοι: Ορισμός, Γεωμετρική ερμηνεία.
• Μερικές παράγωγοι ανωτέρας τάξεως: Ορισμός, Θεώρημα μεικτών παραγώγων.
• Γραμμικοποίηση και Διαφορικά πραγματικών και διανυσματικών συναρτήσεων: Ορισμός, Βασικά θεωρήματα.
• Παράγωγοι κατά κατεύθυνση: Ορισμός, Γεωμετρική ερμηνεία, Ρόλος του διανύσματος κλίσεως.

Λέξεις Κλειδιά: μερικές παράγωγοι, μερικές παράγωγοι ανωτέρας τάξεως, θεώρημα μεικτών παραγώγων, γραμμικοποίηση, διαφόριση, γραμμική συνάρτηση, διαφορικό, παράγωγοι κατά κατεύθυνση

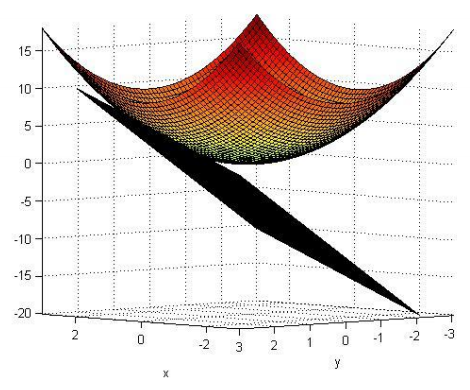
• Ο κανόνας της αλυσιδωτής παραγώγισης.
• Τύπος του Taylor για συναρτήσεις μιας και  πολλών μεταβλητών.
• Εφαπτόμενα επίπεδα.

Λέξεις Κλειδιά: εφαρμογές διαφόρισης, αλυσιδωτή παραγώγιση, εφαπτόμενο επίπεδο, θεώρημα Taylor, θεώρημα πεπλεγμένων συναρτήσεων, κατευθυνόμενη παράγωγος, πολυώνυμο Taylor, τύπος Taylor, σειρά Taylor

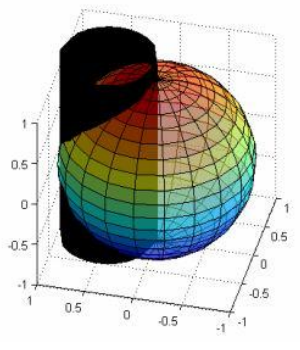
• Διπλά ολοκληρώματα: Καρτεσιανή, Πολική μορφή. Εμβαδά, Μάζα, Ροπές και Κέντρο Μάζας 
• Τριπλά ολοκληρώματα: Καρτεσιανή, Κυλινδρική , Σφαιρική μορφή. Όγκοι, Μάζα, Ροπές και Κέντρο Μάζας.

Λέξεις Κλειδιά: διπλά ολοκληρώματα, τριπλά ολοκληρώματα, ολοκλήρωμα Riemann, θεώρημα Fubini, όγκος στον Rⁿ, μάζες Rⁿ, ροπέςRⁿ, κέντρο βάρουςRⁿ, πολική μορφή, πολικός μετασχηματισμός, κυλινδρικός μετασχηματισμός, κυλινδρική μορφή, σφαιρική μορφή, σφαιρικός μετασχηματισμός, ολοκλήρωμα Gauss

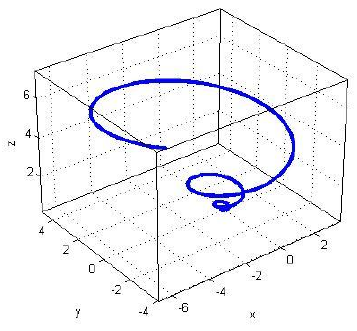
• Επικαμπύλιο Ολοκλήρωμα Ι: Μήκος τόξου, Επικαμπύλιο ολοκλήρωμα πραγματικής συνάρτησης. Μάζα, Ροπές και Κέντρο Μάζας τόξων.
• Επικαμπύλιο Ολοκλήρωμα ΙΙ: Επικαμπύλιο ολοκλήρωμα διανυσματικού πεδίου. Έργο, Ροή, Κυκλοφορία.

Λέξεις Κλειδιά: επικαμπύλιο ολοκλήρωμα, μήκος τόξου, μήκος καμπύλης, επικαμπύλιο ολοκλήρωμα πραγματικής συνάρτησης, επικαμπύλιο ολοκλήρωμα διανυσματικής συνάρτησης

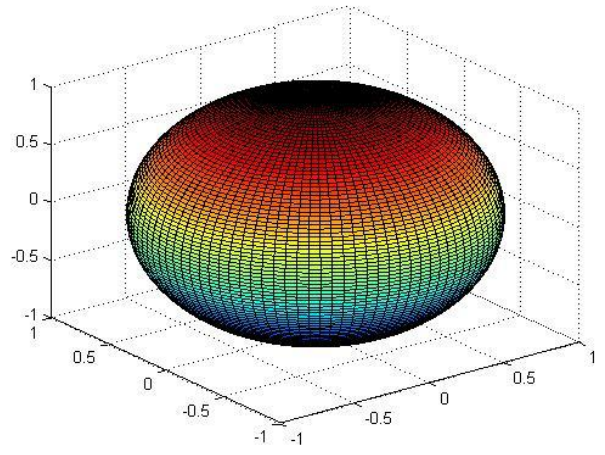
• Επιφανειακό Ολοκλήρωμα Ι: Εμβαδόν επιφανείας, Επιφανειακό ολοκλήρωμα πραγματικής συνάρτησης. Μάζα, Ροπές και Κέντρο Μάζας κελύφους.
• Επιφανειακό Ολοκλήρωμα ΙΙ: Επιφανειακό ολοκλήρωμα διανυσματικού πεδίου. Ροή.

Λέξεις Κλειδιά: επιφανειακό ολοκλήρωμα, εμβαδόν επιφάνειας, εφαπτόμενο επίπεδο, κάθετο διάνυσμα σε επιφάνεια, επιφανειακό ολοκλήρωμα πραγματικής συνάρτησης, επιφανειακό ολοκλήρωμα διανυσματικού πεδίου

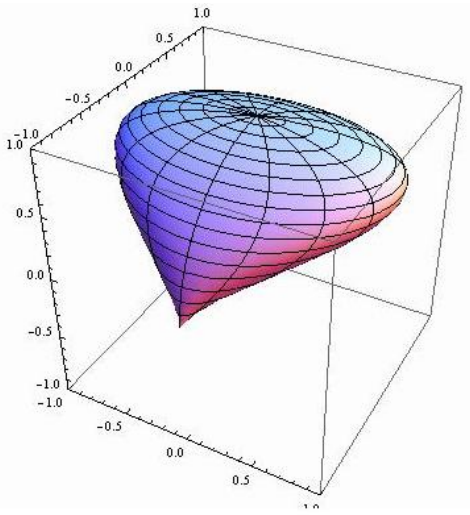
• Διανυσματική Ανάλυση: Τελεστές Κλίσης, Απόκλισης, Στροβιλισμού, Laplace
• Θεώρημα του Green.
• Θεώρημα του Stokes.
• Θεώρημα του Gauss.
• Ανεξαρτησία από τη διαδρομή, Συναρτήσεις Δυναμικού, Συντηρητικά πεδία.

Λέξεις Κλειδιά: διανυσματική ανάλυση, τελεστές κλίσης, τελεστές απόκλισης, τελεστές στροβιλισμού, τελεστής Laplace, θεώρημα Green, θεώρημα Stokes, θεώρημα Gauss, ασυμπίεστα διανυσματικά πεδία, συντηρητικά διανυσματικά πεδία

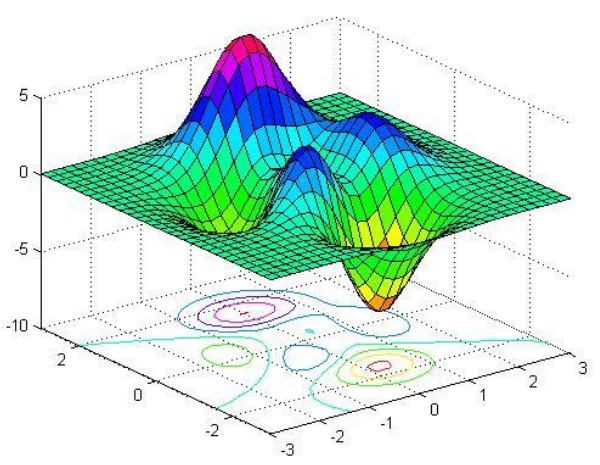
• Ακρότατα και σαγματικά σημεία συναρτήσεων, χωρίς περιορισμούς.
• Μέθοδος των Ελαχίστων Τετραγώνων.

Λέξεις Κλειδιά: τοπικά ακρότατα, ολικά ακρότατα, σαγματικά σημεία, μέθοδος ελαχίστων τετραγώνων