Ουρές Αναμονής
Αντώνιος Οικονόμου
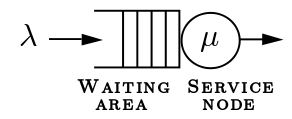
Μια ουρά αναμονής ή ισοδύναμα ένα σύστημα εξυπηρέτησης είναι ένα μαθηματικό πρότυπο για τη μοντελοποίηση ενός πραγματικού συστήματος εισόδου - εξόδου μονάδων (πελατών) στο οποίο υπεισέρχεται τυχαιότητα. Το αντικείμενο του μαθήματος είναι η ποσοτική μελέτη συτημάτων εξυπηρέτησης και εντάσσεται στο ευρύτερο γνωστικό πεδίο της Επιχειρησιακής Έρευνας και ειδικότερα στο στοχαστικό μέρος της.
Τυπικά παραδείγματα ουρών αναμονής που παρουσιάζονται στις εφαρμογές είναι τα ταμεία των τραπεζών και γενικότερα διαφόρων οργανισμών, τα τηλεφωνικά κέντρα εξυπηρέτησης πελατών, το τηλεφωνικό δίκτυο, το διαδίκτυο καθώς και τοπικά δίκτυα υπολογιστών, οι γραμμές παραγωγής μιας βιομηχανικής μονάδας, συγκοινωνιακά δίκτυα κλπ.
Στόχος της θεωρία των ουρών αναμονής είναι η ποσοτική περιγραφή τέτοιων συστημάτων και ο βέλτιστος σχεδιασμός τους. Έτσι η θεωρία ουρών απαντά σε προβλήματα του τύπου
- Πόσο περιμένει κάθε πελάτης κατά μέσο όρο;
- Πόσο είναι το μήκος της ουράς που σχηματίζεται κατά μέσο όρο;
- Πόσο θα μειωθεί κατά μέσο όρο η ουρά αν προστεθεί ένας επιπλέον υπηρέτης;
- Πόσοι υπηρέτες πρέπει να υπάρχουν ώστε η πιθανότητα να υπερχειλίσει το σύστημα να είναι μικρότερη από 1%;

Μια ουρά αναμονής ή ισοδύναμα ένα σύστημα εξυπηρέτησης είναι ένα μαθηματικό πρότυπο για τη μοντελοποίηση ενός πραγματικού συστήματος εισόδου - εξόδου μονάδων (πελατών) στο οποίο υπεισέρχεται τυχαιότητα. Το αντικείμενο του μαθήματος είναι η ποσοτική μελέτη συτημάτων εξυπηρέτησης και εντάσσεται στο ευρύτερο γνωστικό πεδίο της Επιχειρησιακής Έρευνας και ειδικότερα στο στοχαστικό μέρος της.
Τυπικά παραδείγματα ουρών αναμονής που παρουσιάζονται στις εφαρμογές είναι τα ταμεία των τραπεζών και γενικότερα διαφόρων οργανισμών, τα τηλεφωνικά κέντρα εξυπηρέτησης πελατών, το τηλεφωνικό δίκτυο, το διαδίκτυο καθώς και τοπικά δίκτυα υπολογιστών, οι γραμμές παραγωγής μιας βιομηχανικής μονάδας, συγκοινωνιακά δίκτυα κλπ.
Στόχος της θεωρία των ουρών αναμονής είναι η ποσοτική περιγραφή τέτοιων συστημάτων και ο βέλτιστος σχεδιασμός τους. Έτσι η θεωρία ουρών απαντά σε προβλήματα του τύπου
- Πόσο περιμένει κάθε πελάτης κατά μέσο όρο;
- Πόσο είναι το μήκος της ουράς που σχηματίζεται κατά μέσο όρο;
- Πόσο θα με

Μια ουρά αναμονής ή ισοδύναμα ένα σύστημα εξυπηρέτησης είναι ένα μαθηματικό πρότυπο για τη μοντελοποίηση ενός πραγματικού συστήματος εισόδου - εξόδου μονάδων (πελατών) στο οποίο υπεισέρχεται τυχαιότητα. Το αντικείμενο του μαθήματος είναι η ποσοτική μελέτη συτημάτων εξυπηρέτησης και εντάσσεται στο ευρύτερο γνωστικό πεδίο της Επιχειρησιακής Έρευνας και ειδικότερα στο στοχαστικό μέρος της.
Τυπικά παραδείγματα ουρών αναμονής που παρουσιάζονται στις εφαρμογές είναι τα ταμεία των τραπεζών και γενικότερα διαφόρων οργανισμών, τα τηλεφωνικά κέντρα εξυπηρέτησης πελατών, το τηλεφωνικό δίκτυο, το διαδίκτυο καθώς και τοπικά δίκτυα υπολογιστών, οι γραμμές παραγωγής μιας βιομηχανικής μονάδας, συγκοινωνιακά δίκτυα κλπ.
Στόχος της θεωρία των ουρών αναμονής είναι η ποσοτική περιγραφή τέτοιων συστημάτων και ο βέλτιστος σχεδιασμός τους. Έτσι η θεωρία ουρών απαντά σε προβλήματα του τύπου
- Πόσο περιμένει κάθε πελάτης κατά μέσο όρο;
- Πόσο είναι το μήκος της ουράς που σχηματίζεται κατά μέσο όρο;
- Πόσο θα με
Περίγραμμα

Περιεχόμενο μαθήματος
- Περιγραφή των ουρών αναμονής και γενικά αποτελέσματα: βασικά χαρακτηριστικά των ουρών αναμονής, μέτρα λειτουργικότητας και απόδοσης, η διαδικασία μήκους ουράς, εμφυτευμένες διαδικασίες του μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων, η ιδιότητα PASTA, το θεώρημα του Little.
- Απλές Μαρκοβιανές Ουρές: το γενικό μοντέλο, η Μ/Μ/1/1 ουρά, η Μ/Μ/1 ουρά, τροποποιήσεις της Μ/Μ/1 ουράς, η Μ/Μ/k ουρά, το μοντέλο με πεπερασμένο αριθμό δυνητικών πελατών, η διαδικασία αναχωρήσεων της M/M/1 ουράς.
- Μαρκοβιανές Ουρές: η Μ/Μ/1 ουρά με ομαδικές αφίξεις, η Μ/Μ/1 ουρά με ομαδικές αναχωρήσεις, η M/M/k ουρά με ετερογενείς υπηρέτες, η M/M/1/1 ουρά με επαναπροσπάθειες, η Er/Es/1 ουρά και η μέθοδος των φάσεων.
- Μαρκοβιανά δίκτυα ουρών: απλές Μαρκοβιανές ουρές σε σειρά, απλά δίκτυα Μαρκοβιανών ουρών, ανοικτά και κλειστά δίκτυα Jackson.
Μαθησιακοί στόχοι
Σκοπός του μαθήματος είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση πραγματικών συστημάτων εισόδου - εξόδου μονάδων (πελατών) στο οποίο υπεισέρχεται τυχαιότητα..
Έτσι μεσω της θεωρία ουρών ο φοιτητής θα μπορεί να απαντά σε προβλήματα του τύπου
- Πόσο περιμένει κάθε πελάτης κατά μέσο όρο;
- Πόσο είναι το μήκος της ουράς που σχηματίζεται κατά μέσο όρο;
- Πόσο θα μειωθεί κατά μέσο όρο η ουρά αν προστεθεί ένας επιπλέον υπηρέτης;
- Πόσοι υπηρέτες πρέπει να υπάρχουν ώστε η πιθανότητα να υπερχειλίσει το σύστημα να είναι μικρότερη από 1%;
Σχέδιο Μαθήματος
Η ύλη αναπτύσσεται σε τρίωρα μαθήματα. Η κατανομή της ύλης κατά μάθημα είναι η εξής:
- Βασικές έννοιες στα συστήματα εξυπηρέτησης. Συμβολισμός Kendall. Θεμελιώδεις στοχαστικές διαδικασίες και μέτρα απόδοσης. Γενική συνθήκη ευστάθειας. Εμφυτευμένες διαδικασίες μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων. Σχέση των κατανομών ισορροπίας των εμφυτευμένων διαδικασιών στην περίπτωση των μεμονωμένων αφίξεων και αναχωρήσεων. Η ιδιότητα PASTA.
- Το θεώρημα Little. Εφαρμογές της ιδιότητας PASTA και του θεωρήματος Little για υπολογισμούς μέτρων απόδοσης. Επανάληψη βασικών εννοιών και αποτελεσμάτων από τη θεωρία των Μαρκοβιανών αλυσίδων συνεχούς χρόνου, εξισώσεις πλήρους και γενικευμένης ισορροπίας.
- Απλές Μαρκοβιανές Ουρές: Ορισμοί και μορφή γινομένου της στάσιμης κατανομής. Η Μ/Μ/1/1 ουρά. Η Μ/Μ/1 ουρά: κατανομή πλήθους πελατών, κατανομή χρόνου παραμονής πελάτη στο σύστημα. Τροποποιήσεις της Μ/Μ/1 ουράς: γενική σχέση των κατανομών ισορροπίας σε συνεχή χρόνο, σε στιγμές αφίξεων και αναχωρήσεων, υπολογισμός μέσου ρυθμού αφίξεων και αναχωρήσεων και ποσοστού χαμένων πελατών σε συστήματα με απώλειες. Η Μ/Μ/1/s ουρά. Η Μ/Μ/1 ουρά με αποθαρρυνόμενους πελάτες.
- H Μ/Μ/1 ουρά με μεταβλητό ρυθμό εξυπηρέτησης. Η Μ/Μ/k ουρά. Τροποποιήσεις της Μ/Μ/k ουράς: η M/M/k/s και η M/M/k/k ουρά. Το μοντέλο με πεπερασμένο αριθμό δυνητικών πελατών.
- Η μέθοδος των πιθανογεννητριών για την εύρεση της στάσιμης κατανομής Μαρκοβιανών ουρών με πολλαπλές μεταβάσεις. Η Μ/Μ/1 ουρά με ομαδικές αφίξεις. Η ειδική περίπτωση της γεωμετρικής κατανομής για το μέγεθος των αφικνούμενων ομάδων. Η Μ/Μ/1 ουρά με ομαδικές αναχωρήσεις. Ασκήσεις.
- Αντίστροφες στοχαστικές διαδικασίες. Αντιστρέψιμες Μαρκοβιανές αλυσίδες. Η διαδικασία αναχώρησης της Μ/Μ/1 ουράς. Η Μ/Μ/k ουρά με ετερογενείς υπηρέτες. Ασκήσεις.
- Η Μ/Μ/1 ουρά με επαναπροσπάθειες. Ασκήσεις.
- Η Er/Es/1 ουρά και η μέθοδος των φάσεων. H Ε2/Μ/1 ουρά. Η Ε2/Ε2/1/1 ουρά. Η M/Es/1 ουρά. Η Er/M/1 ουρά. Η M/Er/1/1 ουρά. Η M/E2/2/2 ουρά.
- Εισαγωγή στα Μαρκοβιανά δίκτυα ουρών. Βασικοί συμβολισμοί. Πιθανοθεωρητική ανάλυση Μ/Μ/1 ουρών σε σειρά. Δίκτυα Jackson (ανοικτά και κλειστά). Στάσιμη κατανομή δικτύων Jackson. Άλλες κλάσεις Μαρκοβιανών δικτύων: δίκτυα με περιορισμένη χωρητικότητα και πρωτόκολλα παρεμπόδισης. Ασκήσεις.
- Μαρκοβιανά συστήματα εξυπηρέτησης με ιδιαίτερα χαρακτηριστικά. Συστήματα με χρόνους εκκίνησης, συστήματα με υπηρέτες που υπόκεινται σε βλάβες και επισκευές, συστήματα με μεταβλητό αριθμό υπηρετών και πολιτικές υστέρησης για την ενεργοποίηση τους. Ασκήσεις.
- Ανασκόπηση του μαθήματος και επαναληπτικές ασκήσεις
Ομάδα στόχος
Προπτυχιακοί φοιτητές Τμημάτων Μαθηματικών, Στατιστικής, Πληροφορικής και Πολυτεχνικών Σχολών
Μέθοδοι διδασκαλίας
Διδασκαλία καθ΄ έδρας – Ασκήσεις
Μέθοδοι αξιολόγησης
Εξετάσεις (2 ώρες και 30 λεπτά)
Προτεινόμενα συγγράμματα
- Φακίνου Δ. (2003) Ουρές Αναμονής. Αθήνα. (Διανέμεται σε όσους δηλώσουν το μάθημα)
Βιβλιογραφία
- Φακίνου Δ. (2003) Ουρές Αναμονής. Αθήνα. (Διανέμεται σε όσους δηλώσουν το μάθημα)
- Myron Hlynka's Queueing Theory Page (Ιστοσελίδα με πλήθος πληροφοριών για τις ουρές Αναμονής, σημειώσεις και βιβλία από προπτυχιακά και μεταπτυχιακά μαθήματα στη Θεωρία Ουρών από όλο τον κόσμο.)
Προαπαιτούμενα
Για την ουσιαστική μελέτη τέτοιων συστημάτων το βασικό εργαλείο είναι η Θεωρία Πιθανοτήτων και Στοχαστικών Ανελίξεων, αφού τα μαθηματικά πρότυπα των ουρών αναμονής είναι στοχαστικά (τυχαιοκρατικά). Για να είναι ένας φοιτητής σε θέση να παρακολουθήσει με επιτυχία το μάθημα θα πρέπει να έχει παρακολουθήσει και κατανοήσει επαρκώς τα μαθήματα Πιθανότητες Ι, ΙΙ και Στοχαστικές Μέθοδοι στην Επιχειρησιακή Έρευνα Ι ή Στοχαστικές Ανελίξεις. Κατά τη διάρκεια της διδασκαλίας θα γίνει ανασκόπηση των εννοιών από τις στοχαστικές διαδικασίες που χρειάζονται ώστε να είναι δυνατό να παρακολουθήσει το μάθημα κάποιος φοιτητής, χωρίς να έχει ποτέ παρακολουθήσει τις Στοχαστικές Μεθόδους στην Επιχειρησιακή Έρευνα ή τις Στοχαστικές Ανελίξεις. Στην περίπτωση αυτή όμως θα πρέπει ο φοιτητής να καταβάλει επιπλέον προσπάθεια και το ιδανικό θα ήταν να παρακολουθήσει ταυτόχρονα και τις Στοχαστικές Ανελίξεις ή τις Στοχαστικές Μεθόδους στην Επιχειρησιακή Έρευνα Ι.
Διδάσκοντες
 Αντώνης Οικονόμου
Αντώνης Οικονόμου
Αναπληρωτής Καθηγητής
Καποδιαστριακό Πανεπιστήμιο Αθηνών
Τμήμα Μαθηματικών, Τομέας Στατιστικής και Επιχειρησιακής Έρευνας
Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Σπουδές: Πτυχίο Μαθηματικών Πανεπιστημίου Αθηνών (1993), Μεταπτυχιακό στα Θεωρητικά Μαθηματικά UCLA (1994), Μεταπτυχιακό στη Στατιστική και Επιχειρησιακή Έρευνα Πανεπιστημίου Αθηνών (1997) και Διδακτορικό στα Μαθηματικά Πανεπιστημίου Αθηνών (1998). Ερευνητικά ενδιαφέροντα: Πιθανότητες, Επιχειρησιακή Έρευνα, Μαθηματική Βιολογία. Ειδικότερα, προβλήματα υπολογισμών, στοχαστικών συγκρίσεων και βελτιστοποίησης σε στοχαστικές διαδικασίες με εφαρμογές στη θεωρία συστημάτων εξυπηρέτησης (θεωρία ουρών) και στα στοχαστικά πρότυπα εξέλιξης πληθυσμών.
- Περιγραφή των ουρών αναμονής και γενικά αποτελέσματα: βασικά χαρακτηριστικά των ουρών αναμονής, μέτρα λειτουργικότητας και απόδοσης, η διαδικασία μήκους ουράς, εμφυτευμένες διαδικασίες του μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων, η ιδιότητα PASTA, το θεώρημα του Little.
- Απλές Μαρκοβιανές Ουρές: το γενικό μοντέλο, η Μ/Μ/1/1 ουρά, η Μ/Μ/1 ουρά, τροποποιήσεις της Μ/Μ/1 ουράς, η Μ/Μ/k ουρά, το μοντέλο με πεπερασμένο αριθμό δυνητικών πελατών, η διαδικασία αναχωρήσεων της M/M/1 ουράς.
- Μαρκοβιανές Ουρές: η Μ/Μ/1 ουρά με ομαδικές αφίξεις, η Μ/Μ/1 ουρά με ομαδικές αναχωρήσεις, η M/M/k ουρά με ετερογενείς υπηρέτες, η M/M/1/1 ουρά με επαναπροσπάθειες, η Er/Es/1 ουρά και η μέθοδος των φάσεων.
- Μαρκοβιανά δίκτυα ουρών: απλές Μαρκοβιανές ουρές σε σειρά, απλά δίκτυα Μαρκοβιανών ουρών, ανοικτά και κλειστά δίκτυα Jackson.
Σκοπός του μαθήματος είναι η ανάπτυξη βασικών δεξιοτήτων για τη μοντελοποίηση και τη μαθηματική ανάλυση πραγματικών συστημάτων εισόδου - εξόδου μονάδων (πελατών) στο οποίο υπεισέρχεται τυχαιότητα..
Έτσι μεσω της θεωρία ουρών ο φοιτητής θα μπορεί να απαντά σε προβλήματα του τύπου
- Πόσο περιμένει κάθε πελάτης κατά μέσο όρο;
- Πόσο είναι το μήκος της ουράς που σχηματίζεται κατά μέσο όρο;
- Πόσο θα μειωθεί κατά μέσο όρο η ουρά αν προστεθεί ένας επιπλέον υπηρέτης;
- Πόσοι υπηρέτες πρέπει να υπάρχουν ώστε η πιθανότητα να υπερχειλίσει το σύστημα να είναι μικρότερη από 1%;
Η ύλη αναπτύσσεται σε τρίωρα μαθήματα. Η κατανομή της ύλης κατά μάθημα είναι η εξής:
- Βασικές έννοιες στα συστήματα εξυπηρέτησης. Συμβολισμός Kendall. Θεμελιώδεις στοχαστικές διαδικασίες και μέτρα απόδοσης. Γενική συνθήκη ευστάθειας. Εμφυτευμένες διαδικασίες μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων. Σχέση των κατανομών ισορροπίας των εμφυτευμένων διαδικασιών στην περίπτωση των μεμονωμένων αφίξεων και αναχωρήσεων. Η ιδιότητα PASTA.
- Το θεώρημα Little. Εφαρμογές της ιδιότητας PASTA και του θεωρήματος Little για υπολογισμούς μέτρων απόδοσης. Επανάληψη βασικών εννοιών και αποτελεσμάτων από τη θεωρία των Μαρκοβιανών αλυσίδων συνεχούς χρόνου, εξισώσεις πλήρους και γενικευμένης ισορροπίας.
- Απλές Μαρκοβιανές Ουρές: Ορισμοί και μορφή γινομένου της στάσιμης κατανομής. Η Μ/Μ/1/1 ουρά. Η Μ/Μ/1 ουρά: κατανομή πλήθους πελατών, κατανομή χρόνου παραμονής πελάτη στο σύστημα. Τροποποιήσεις της Μ/Μ/1 ουράς: γενική σχέση των κατανομών ισορροπίας σε συνεχή χρόνο, σε στιγμές αφίξεων και αναχωρήσεων, υπολογισμός μέσου ρυθμού αφίξεων και αναχωρήσεων και ποσοστού χαμένων πελατών σε συστήματα με απώλειες. Η Μ/Μ/1/s ουρά. Η Μ/Μ/1 ουρά με αποθαρρυνόμενους πελάτες.
- H Μ/Μ/1 ουρά με μεταβλητό ρυθμό εξυπηρέτησης. Η Μ/Μ/k ουρά. Τροποποιήσεις της Μ/Μ/k ουράς: η M/M/k/s και η M/M/k/k ουρά. Το μοντέλο με πεπερασμένο αριθμό δυνητικών πελατών.
- Η μέθοδος των πιθανογεννητριών για την εύρεση της στάσιμης κατανομής Μαρκοβιανών ουρών με πολλαπλές μεταβάσεις. Η Μ/Μ/1 ουρά με ομαδικές αφίξεις. Η ειδική περίπτωση της γεωμετρικής κατανομής για το μέγεθος των αφικνούμενων ομάδων. Η Μ/Μ/1 ουρά με ομαδικές αναχωρήσεις. Ασκήσεις.
- Αντίστροφες στοχαστικές διαδικασίες. Αντιστρέψιμες Μαρκοβιανές αλυσίδες. Η διαδικασία αναχώρησης της Μ/Μ/1 ουράς. Η Μ/Μ/k ουρά με ετερογενείς υπηρέτες. Ασκήσεις.
- Η Μ/Μ/1 ουρά με επαναπροσπάθειες. Ασκήσεις.
- Η Er/Es/1 ουρά και η μέθοδος των φάσεων. H Ε2/Μ/1 ουρά. Η Ε2/Ε2/1/1 ουρά. Η M/Es/1 ουρά. Η Er/M/1 ουρά. Η M/Er/1/1 ουρά. Η M/E2/2/2 ουρά.
- Εισαγωγή στα Μαρκοβιανά δίκτυα ουρών. Βασικοί συμβολισμοί. Πιθανοθεωρητική ανάλυση Μ/Μ/1 ουρών σε σειρά. Δίκτυα Jackson (ανοικτά και κλειστά). Στάσιμη κατανομή δικτύων Jackson. Άλλες κλάσεις Μαρκοβιανών δικτύων: δίκτυα με περιορισμένη χωρητικότητα και πρωτόκολλα παρεμπόδισης. Ασκήσεις.
- Μαρκοβιανά συστήματα εξυπηρέτησης με ιδιαίτερα χαρακτηριστικά. Συστήματα με χρόνους εκκίνησης, συστήματα με υπηρέτες που υπόκεινται σε βλάβες και επισκευές, συστήματα με μεταβλητό αριθμό υπηρετών και πολιτικές υστέρησης για την ενεργοποίηση τους. Ασκήσεις.
- Ανασκόπηση του μαθήματος και επαναληπτικές ασκήσεις
Προπτυχιακοί φοιτητές Τμημάτων Μαθηματικών, Στατιστικής, Πληροφορικής και Πολυτεχνικών Σχολών
Διδασκαλία καθ΄ έδρας – Ασκήσεις
Εξετάσεις (2 ώρες και 30 λεπτά)
- Φακίνου Δ. (2003) Ουρές Αναμονής. Αθήνα. (Διανέμεται σε όσους δηλώσουν το μάθημα)
- Φακίνου Δ. (2003) Ουρές Αναμονής. Αθήνα. (Διανέμεται σε όσους δηλώσουν το μάθημα)
- Myron Hlynka's Queueing Theory Page (Ιστοσελίδα με πλήθος πληροφοριών για τις ουρές Αναμονής, σημειώσεις και βιβλία από προπτυχιακά και μεταπτυχιακά μαθήματα στη Θεωρία Ουρών από όλο τον κόσμο.)
Για την ουσιαστική μελέτη τέτοιων συστημάτων το βασικό εργαλείο είναι η Θεωρία Πιθανοτήτων και Στοχαστικών Ανελίξεων, αφού τα μαθηματικά πρότυπα των ουρών αναμονής είναι στοχαστικά (τυχαιοκρατικά). Για να είναι ένας φοιτητής σε θέση να παρακολουθήσει με επιτυχία το μάθημα θα πρέπει να έχει παρακολουθήσει και κατανοήσει επαρκώς τα μαθήματα Πιθανότητες Ι, ΙΙ και Στοχαστικές Μέθοδοι στην Επιχειρησιακή Έρευνα Ι ή Στοχαστικές Ανελίξεις. Κατά τη διάρκεια της διδασκαλίας θα γίνει ανασκόπηση των εννοιών από τις στοχαστικές διαδικασίες που χρειάζονται ώστε να είναι δυνατό να παρακολουθήσει το μάθημα κάποιος φοιτητής, χωρίς να έχει ποτέ παρακολουθήσει τις Στοχαστικές Μεθόδους στην Επιχειρησιακή Έρευνα ή τις Στοχαστικές Ανελίξεις. Στην περίπτωση αυτή όμως θα πρέπει ο φοιτητής να καταβάλει επιπλέον προσπάθεια και το ιδανικό θα ήταν να παρακολουθήσει ταυτόχρονα και τις Στοχαστικές Ανελίξεις ή τις Στοχαστικές Μεθόδους στην Επιχειρησιακή Έρευνα Ι.
 Αντώνης Οικονόμου
Αντώνης Οικονόμου
Αναπληρωτής Καθηγητής
Καποδιαστριακό Πανεπιστήμιο Αθηνών
Τμήμα Μαθηματικών, Τομέας Στατιστικής και Επιχειρησιακής Έρευνας
Ο Αντώνης Οικονόμου είναι μέλος ΔΕΠ στον Τομέα Στατιστικής και Επιχειρησιακής Έρευνας του Τμήματος Μαθηματικών του Πανεπιστημίου Αθηνών από το 2001.
Σπουδές: Πτυχίο Μαθηματικών Πανεπιστημίου Αθηνών (1993), Μεταπτυχιακό στα Θεωρητικά Μαθηματικά UCLA (1994), Μεταπτυχιακό στη Στατιστική και Επιχειρησιακή Έρευνα Πανεπιστημίου Αθηνών (1997) και Διδακτορικό στα Μαθηματικά Πανεπιστημίου Αθηνών (1998). Ερευνητικά ενδιαφέροντα: Πιθανότητες, Επιχειρησιακή Έρευνα, Μαθηματική Βιολογία. Ειδικότερα, προβλήματα υπολογισμών, στοχαστικών συγκρίσεων και βελτιστοποίησης σε στοχαστικές διαδικασίες με εφαρμογές στη θεωρία συστημάτων εξυπηρέτησης (θεωρία ουρών) και στα στοχαστικά πρότυπα εξέλιξης πληθυσμών.
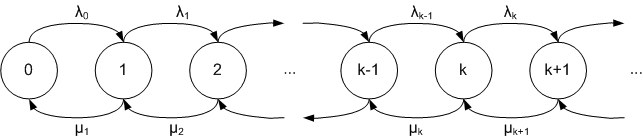
 Βασικές έννοιες στα συστήματα εξυπηρέτησης. Συμβολισμός Kendall. Θεμελιώδεις στοχαστικές διαδικασίες και μέτρα απόδοσης. Γενική συνθήκη ευστάθειας. Εμφυτευμένες διαδικασίες μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων. Σχέση των κατανομών ισορροπίας των εμφυτευμένων διαδικασιών στην περίπτωση των μεμονωμένων αφίξεων και αναχωρήσεων. Η ιδιότητα PASTA. Το θεώρημα Little. Εφαρμογές της ιδιότητας PASTA και του θεωρήματος Little για υπολογισμούς μέτρων απόδοσης. Επανάληψη βασικών εννοιών και αποτελεσμάτων από τη θεωρία των Μαρκοβιανών αλυσίδων συνεχούς χρόνου, εξισώσεις πλήρους και γενικευμένης ισορροπίας.
Βασικές έννοιες στα συστήματα εξυπηρέτησης. Συμβολισμός Kendall. Θεμελιώδεις στοχαστικές διαδικασίες και μέτρα απόδοσης. Γενική συνθήκη ευστάθειας. Εμφυτευμένες διαδικασίες μήκους ουράς σε στιγμές αφίξεων και αναχωρήσεων. Σχέση των κατανομών ισορροπίας των εμφυτευμένων διαδικασιών στην περίπτωση των μεμονωμένων αφίξεων και αναχωρήσεων. Η ιδιότητα PASTA. Το θεώρημα Little. Εφαρμογές της ιδιότητας PASTA και του θεωρήματος Little για υπολογισμούς μέτρων απόδοσης. Επανάληψη βασικών εννοιών και αποτελεσμάτων από τη θεωρία των Μαρκοβιανών αλυσίδων συνεχούς χρόνου, εξισώσεις πλήρους και γενικευμένης ισορροπίας.
Λέξεις-Κλειδιά: βασικά χαρακτηριστικά των ουρών αναμονής, μέτρα λειτουργικότητας και απόδοσης, η διαδικασία μήκους ουράς
Απλές Μαρκοβιανές Ουρές: Ορισμοί και μορφή γινομένου της στάσιμης κατανομής. Η Μ/Μ/1/1 ουρά. Η Μ/Μ/1 ουρά: κατανομή πλήθους πελατών, κατανομή χρόνου παραμονής πελάτη στο σύστημα.
Τροποποιήσεις της Μ/Μ/1 ουράς: γενική σχέση των κατανομών ισορροπίας σε συνεχή χρόνο, σε στιγμές αφίξεων και αναχωρήσεων, υπολογισμός μέσου ρυθμού αφίξεων και αναχωρήσεων και ποσοστού χαμένων πελατών σε συστήματα με απώλειες. Η Μ/Μ/1/s ουρά. Η Μ/Μ/1 ουρά με αποθαρρυνόμενους πελάτες.
Λέξεις-Κλειδιά: Απλές Μαρκοβιανές ουρές, στάσιμη κατανομή, Μ/Μ/1 ουρές, κατανομές ισορροπίας
H Μ/Μ/1 ουρά με μεταβλητό ρυθμό εξυπηρέτησης. Η Μ/Μ/k ουρά. Τροποποιήσεις της Μ/Μ/k ουράς: η M/M/k/s και η M/M/k/k ουρά. Το μοντέλο με πεπερασμένο αριθμό δυνητικών πελατών.
Η μέθοδος των πιθανογεννητριών για την εύρεση της στάσιμης κατανομής Μαρκοβιανών ουρών με πολλαπλές μεταβάσεις. Η Μ/Μ/1 ουρά με ομαδικές αφίξεις. Η ειδική περίπτωση της γεωμετρικής κατανομής για το μέγεθος των αφικνούμενων ομάδων. Η Μ/Μ/1 ουρά με ομαδικές αναχωρήσεις. Ασκήσεις.
Λέξεις - Κλειδιά: Μ/Μ/1 ουρά, M/M/k/s και η M/M/k/k ουρά, Μ/Μ/1 ουρά με ομαδικές αφίξεις
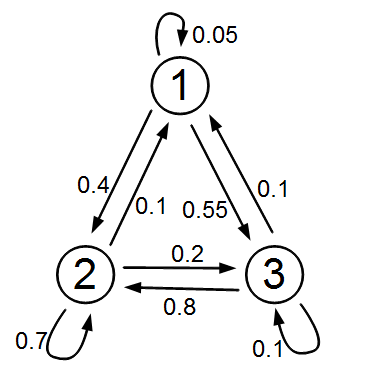
Αντίστροφες στοχαστικές διαδικασίες. Αντιστρέψιμες Μαρκοβιανές αλυσίδες. Η διαδικασία αναχώρησης της Μ/Μ/1 ουράς. Η Μ/Μ/k ουρά με ετερογενείς υπηρέτες. Ασκήσεις.
Η Μ/Μ/1 ουρά με επαναπροσπάθειες. Ασκήσεις.
Η Er/Es/1 ουρά και η μέθοδος των φάσεων. H Ε2/Μ/1 ουρά. Η Ε2/Ε2/1/1 ουρά. Η M/Es/1 ουρά. Η Er/M/1 ουρά. Η M/Er/1/1 ουρά. Η M/E2/2/2 ουρά.
Λέξεις - Κλειδιά: Μ/Μ/k ουρά με ετερογενείς υπηρέτες, Ε2/Ε2/1/1 ουρά, M/Es/1 ουρά, Er/M/1 ουρά, M/Er/1/1 ουρά. M/E2/2/2 ουρά
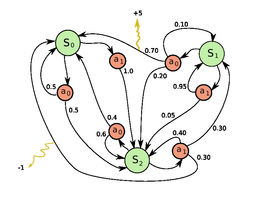 Εισαγωγή στα Μαρκοβιανά δίκτυα ουρών. Βασικοί συμβολισμοί. Πιθανοθεωρητική ανάλυση Μ/Μ/1 ουρών σε σειρά. Δίκτυα Jackson (ανοικτά και κλειστά).
Εισαγωγή στα Μαρκοβιανά δίκτυα ουρών. Βασικοί συμβολισμοί. Πιθανοθεωρητική ανάλυση Μ/Μ/1 ουρών σε σειρά. Δίκτυα Jackson (ανοικτά και κλειστά).
Στάσιμη κατανομή δικτύων Jackson. Άλλες κλάσεις Μαρκοβιανών δικτύων: δίκτυα με περιορισμένη χωρητικότητα και πρωτόκολλα παρεμπόδισης. Ασκήσεις.
Λέξεις - Κλειδιά: Μαρκοβιανά δίκτυα ουρών, Πιθανοθεωρητική ανάλυση Μ/Μ/1 ουράς, Δίκτυα Jackson , στάσιμη κατανομή δικτύων Jackson.

Μαρκοβιανά συστήματα εξυπηρέτησης με ιδιαίτερα χαρακτηριστικά. Συστήματα με χρόνους εκκίνησης, συστήματα με υπηρέτες που υπόκεινται σε βλάβες και επισκευές, συστήματα με μεταβλητό αριθμό υπηρετών και πολιτικές υστέρησης για την ενεργοποίηση τους.
Λέξεις - Κλειδιά: Μαρκοβιανά συστήματα εξυπηρέτησης , Συστήματα με χρόνους εκκίνησης, συστήματα με μεταβλητό αριθμό υπηρετών
Ανοικτό Ακαδ. Μάθημα

Αρ. Επισκέψεων : 0
Αρ. Προβολών : 0
Ημερολόγιο
Ανακοινώσεις
- - Δεν υπάρχουν ανακοινώσεις -
